Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Квадратный корень из степени - СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ - КВАДРАТНЫЕ КОРНИ
Цель: рассмотреть извлечение квадратного корня из степени числа.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Сформулируйте и запишите теорему о квадратном корне из произведения чисел.
2. Вычислите значение выражения:
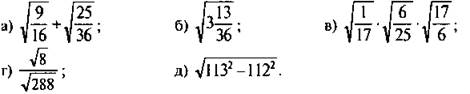
Вариант 2
1. Сформулируйте и запишите теорему о квадратном корне из частного.
2. Вычислите значение выражения:
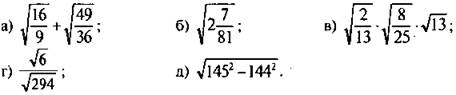
III. Изучение нового материала (основные понятия)
Сначала рассмотрим числовые примеры. Найдем значение выражения ![]() при х = 8 и при х = -7. Получаем:
при х = 8 и при х = -7. Получаем: ![]() В каждом из этих примеров корень из квадрата числа равнялся модулю этого числа:
В каждом из этих примеров корень из квадрата числа равнялся модулю этого числа: ![]() Обобщим результаты этих примеров и докажем теорему.
Обобщим результаты этих примеров и докажем теорему.
Теорема: при любом значении х верно равенство ![]()
Рассмотрим два случая.
а) Если x ≥ 0, то по определению арифметического корня ![]() Так как х ≥ 0, то х = |х| и равенство может быть записано в виде
Так как х ≥ 0, то х = |х| и равенство может быть записано в виде ![]()
б) Если х < 0, то величина -х > 0 и получаем ![]() Так как х < 0, то -x = |х| и равенство можно записать в виде
Так как х < 0, то -x = |х| и равенство можно записать в виде ![]()
Значит, при любом значении х выполнено равенство ![]()
Такое тождество очень часто применяется при извлечении квадратного корня из степени с четным показателем. При этом, чтобы извлечь корень из степени с четным показателем, надо представить подкоренное выражение в виде квадрата некоторого выражения и использовать рассмотренное тождество.
Пример 1
Извлечем корень ![]()
Представим степень а8 в виде квадрата степени а4, т. е. a8 = (a4)2 и используем тождество: ![]() Учтено, что при всех значениях а величина а4 ≥ 0 и |а4| = а4.
Учтено, что при всех значениях а величина а4 ≥ 0 и |а4| = а4.
Пример 2
Извлечем корень ![]() при с < 0.
при с < 0.
Представим с6 в виде с6 = (c3)2 и используем тождество. Получаем ![]() Учтено, что с < 0, тогда с3 < 0 и |с3| = -с3 (по определению модуля).
Учтено, что с < 0, тогда с3 < 0 и |с3| = -с3 (по определению модуля).
Пример 3
Найдем значение выражения ![]()
Разложим число 63504 на произведение простых множителей и получим: 63504 = 24 · 34 · 72. Теперь найдем ![]()
![]()
Полученное тождество позволяет решать и более сложные задачи.
Пример 4
Найдем значение выражения ![]()
Учтем теорему о корне из произведения и формулу разности квадратов.
Получаем: ![]()
![]()
Пример 5
Докажем, что значение выражения ![]() является целым числом.
является целым числом.
В каждом подкоренном выражении выделим квадраты разности чисел: ![]()
![]() Теперь преобразуем данное выражение:
Теперь преобразуем данное выражение: ![]()
![]() Было учтено, что
Было учтено, что ![]() (для оценок можно считать
(для оценок можно считать ![]() ). Поэтому
). Поэтому ![]()
![]()
![]() Итак, значение данного выражения является целым (и даже натуральным) числом 2.
Итак, значение данного выражения является целым (и даже натуральным) числом 2.
Пример 6
Решим уравнение ![]()
Учтем, что подкоренное выражение является полным квадратом разности. Поэтому получаем: ![]() Если модуль некоторой величины равен 5, то сама величина будет равна ±5. Имеем два линейных уравнения: x - 3 = 5 (корень х = 8) и х - 3 = -5 (корень х = -2). Итак, данное уравнение имеет два корня х = 8 и х = -2.
Если модуль некоторой величины равен 5, то сама величина будет равна ±5. Имеем два линейных уравнения: x - 3 = 5 (корень х = 8) и х - 3 = -5 (корень х = -2). Итак, данное уравнение имеет два корня х = 8 и х = -2.
Пример 7
Докажем, что при х ∈ [-1; 4] значения выражения ![]()
![]() не зависят от величины х.
не зависят от величины х.
Подкоренные выражения являются квадратами суммы и разности соответственно. Преобразуем данное выражение: ![]()
![]() Учтено, что при х ∈ [-1; 4] величина х + 1 ≥ 0 и |х + 1| = х + 1; х – 4 ≤ 0 и |х - 4| = -(-х - 4).
Учтено, что при х ∈ [-1; 4] величина х + 1 ≥ 0 и |х + 1| = х + 1; х – 4 ≤ 0 и |х - 4| = -(-х - 4).
Действительно, значения данного выражения равны одному и тому же числу 5 (т. е. не зависят от х).
IV. Контрольные вопросы
1. Сформулируйте и докажите теорему о корне из квадрата числа (выражения).
2. Как извлечь корень из степени с четным показателем?
V. Задание на уроке
№ 384 (а, б); 386 (в); 388 (а, в); 389 (б, в); 391 (б); 393 (в, д, ж); 394 (а, б).
VI. Задание на дом
№ 384 (в, г); 386 (г); 388 (б, г); 389 (г, е); 391 (е); 393 (г, е, з); 394 (в, г).
VII. Творческие задания
1. Найдите значение выражения:
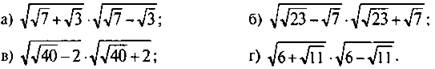
Ответы: а) 2; б) 4; в) 6; г) 5.
2. Упростите выражение:
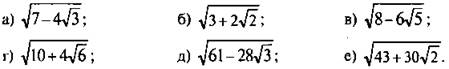
Ответы: ![]()
3. Вычислите:

Ответы: а) 5; б) 6; в) 1; г) 6.
4. Решите уравнение:
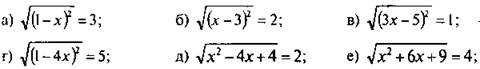
![]()
Ответы: а) х1 = -2 и х2 = 4; б) х1 = 1 и х2 = 5; в) х1 = 4/3 и х2 = 2; г) х1 = -1 и х2 = 1,5; д) x1 = 0 и х2 = 4; е) х1 = -7 и х2 = 1; ж) х1 = -1/3 и х2 = 1; з) х1 = 0,5 и х2 = 1.
5. Упростите выражение:
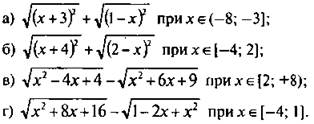
Ответы: а) -2х - 2; б) 6; в) -5; г) 2х + 3.
6. Решите неравенство:
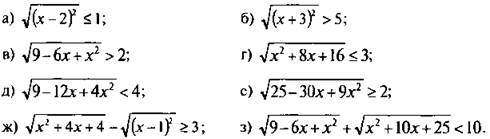
Ответы: ![]()
![]()
VIII. Подведение итогов урока