Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Преобразование выражений, содержащих квадратные корни - ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ - КВАДРАТНЫЕ КОРНИ
Цель: рассмотреть основные приемы преобразования иррациональных выражений.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Вынесите множитель из-под знака корня:
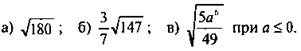
2. Внесите множитель под знак корня.
![]()
3. Сравните значения выражений ![]()
Вариант 2
1. Вынесите множитель из-под знака корня:
![]()
2. Внесите множитель под знак корня:
![]()
3. Сравните значения выражений ![]()
III. Изучение нового материала (основные понятия)
В процессе изучения были рассмотрены тождественные преобразования иррациональных выражений. К ним относятся: преобразования корней из произведения, дроби и степени; умножение и деление корней; вынесение множителя из-под знака корня; внесение множителя под знак корня. Рассмотрим другие примеры тождественных преобразований иррациональных выражений.
Пример 1
Упростим выражение ![]()
Данное выражение имеет смысл при а ≥ 0. Учитывая свойства корней, вынесем множители из-под знаков корня. Получаем
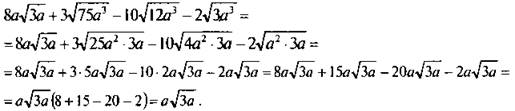
Заметим, что на последнем этапе в выражение были приведены подобные члены.
Пример 2
Преобразуем произведение ![]()
Умножим каждый член в первой скобке на каждый член во второй (аналогично произведению многочленов) и получим: ![]()
![]()
Заметим, что вычисления можно упростить, если из первой скобки вынести множитель 4 и использовать формулу разности квадратов. Получаем: ![]()
![]()
Пример 3
Сократим дробь ![]()
Учтем, что ![]() Тогда числитель дроби можно разложить на множители, используя формулу разности квадратов. Получаем:
Тогда числитель дроби можно разложить на множители, используя формулу разности квадратов. Получаем: 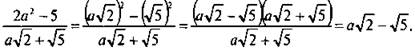
Пример 4
Сократим дробь ![]()
Разложим на множители числитель дроби, используя формулу разности квадратов, и знаменатель дроби, используя формулу квадрата разности. Получаем: 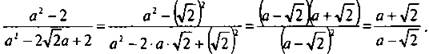
Достаточно часто приходится избавляться от иррациональности в знаменателе (или числителе) дроби. Для этого числитель и знаменатель умножают на сопряженную величину, т. е. такую величину, чтобы знаменатель (или числитель) не содержал иррациональных выражений.
Пример 5
Избавимся от иррациональности в знаменатели дроби ![]() .
.
Очевидно, что знаменатель дроби не будет содержать знака квадратного корня, если числитель и знаменатель дроби умножить на величину ![]() (которая является величиной, сопряженной знаменателю, в этом случае).
(которая является величиной, сопряженной знаменателю, в этом случае).
Получаем: 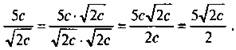 Мы заменили дробь
Мы заменили дробь ![]() (содержащую иррациональность
(содержащую иррациональность ![]() в знаменателе) тождественно равной дробью
в знаменателе) тождественно равной дробью ![]() (которая уже не содержит иррациональности в знаменателе). Тем самым мы освободились от иррациональности в знаменателе дроби.
(которая уже не содержит иррациональности в знаменателе). Тем самым мы освободились от иррациональности в знаменателе дроби.
Пример 6
Избавимся от иррациональности в числителе дроби ![]()
Чтобы избавиться от иррациональности в числителе дроби ![]() , надо умножить числитель и знаменатель на величину
, надо умножить числитель и знаменатель на величину ![]() (которая является сопряженной числителю величиной). При этом в числителе возникает разность квадратов чисел, которая и приводит к исчезновению квадратных корней в числителе. Получаем:
(которая является сопряженной числителю величиной). При этом в числителе возникает разность квадратов чисел, которая и приводит к исчезновению квадратных корней в числителе. Получаем: 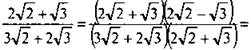
![]() Таким образом, дробь
Таким образом, дробь 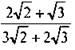 (содержащая иррациональность
(содержащая иррациональность ![]() в числителе) была заменена тождественно равной дробью
в числителе) была заменена тождественно равной дробью ![]() (которая не содержит иррациональности в числителе). Тем самым мы избавились от иррациональности в числителе.
(которая не содержит иррациональности в числителе). Тем самым мы избавились от иррациональности в числителе.
Заметим, что подобные навыки избавления от иррациональности полезны и при решении более сложных задач.
Пример 7
Найдем сумму дробей ![]()
В каждой дроби избавимся от иррациональности в знаменателе, умножив ее числитель и знаменатель на величину, сопряженную знаменателю. Получаем: 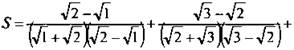
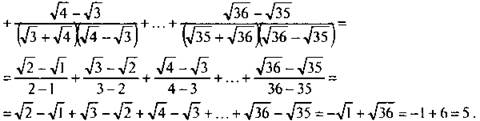
Видно, что после избавления от иррациональности знаменатели всех дробей равны 1. В полученной сумме сокращаются все слагаемые, кроме -√1 и √36. В итоге получаем, что сумма всех данных иррациональных дробей равна натуральному числу 5.
Пример 8
Найдем наибольшее значение дроби ![]()
Допустимые значения переменной в данной дроби a ≥ 3, a ≠ 4. Избавимся от иррациональности в числителе дроби А, умножив ее числитель и знаменатель на сопряженную величину ![]() . Получаем:
. Получаем: 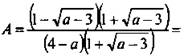
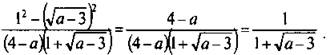 Так как числитель не зависит от переменной, а знаменатель — зависит, то дробь принимает наибольшее значение, если имеет наименьший знаменатель
Так как числитель не зависит от переменной, а знаменатель — зависит, то дробь принимает наибольшее значение, если имеет наименьший знаменатель ![]() . По определению арифметического квадратного корня
. По определению арифметического квадратного корня ![]() Тогда наименьшее значение знаменателя
Тогда наименьшее значение знаменателя ![]() равно 1 и достигается при a = 3. Следовательно, наибольшее значение данной дроби А равно 1 и достигается при а = 3.
равно 1 и достигается при a = 3. Следовательно, наибольшее значение данной дроби А равно 1 и достигается при а = 3.
При преобразовании иррациональных выражений часто полезно ввести новую переменную (сделать замену переменной).
Пример 9
Упростим выражение 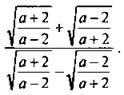
Видно, что в данное выражение входит или величина 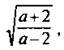 или обратная ей величина
или обратная ей величина ![]() Поэтому введем новую переменную
Поэтому введем новую переменную ![]() (очевидно,
(очевидно, ![]() ), тогда
), тогда ![]() После этого данное выражение имеет вид:
После этого данное выражение имеет вид: 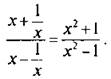 Теперь подставим значение х2 и получим:
Теперь подставим значение х2 и получим: 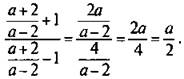 Итак, данное выражение равно a/2.
Итак, данное выражение равно a/2.
IV. Задание на уроке
№ 418 (а, е); 420 (г); 422 (д); 423 (а, д); 425 (б, д); 427 (в, д); 429 (в, е); 431 (д); 433 (в, д).
V. Задание на дом
№ 418 (б, ж); 421 (в); 422 (е); 423 (б, е); 425 (в, е); 427 (г, е); 429 (г, и); 431 (е); 433 (г, е).
VI. Творческие задания
1. Сравните значения числовых выражений:
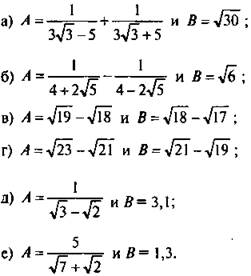
Ответы: а-г) A < В; д) А > В; е) А < В. Указания: а, б) для числа А выполните действия; в, г) умножьте и разделите числа А и В на сопряженные; д, е) избавьтесь от иррациональности в знаменателе числа А.
2. Найдите наибольшее значение выражения. При каком значении a оно достигается?
![]()
Ответы: а) 1/2 при a = 4; б) 1/3 при a = -2 (указание: избавьтесь от иррациональности в числителе).
3. Найдите наименьшее значение выражения. При каком значении a оно достигается?
![]()
Ответы: а) 3 при a = ±2; б) 5 при a = ± 1 (указание: избавьтесь от
иррациональности в знаменателе).
4. Найти величину ![]() если
если ![]() .
.
Ответ: 6 (указание: возвести в квадрат равенство ![]() ).
).
5. Найти сумму ![]() , если разность
, если разность ![]() . Ответ: 5 (указание: умножить равенство
. Ответ: 5 (указание: умножить равенство ![]() на выражение
на выражение ![]() ).
).
6. Упростите выражение:
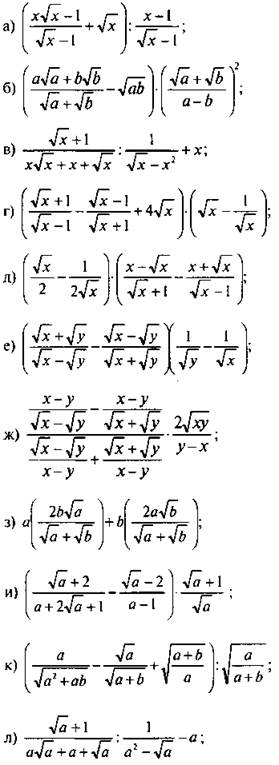
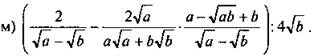
Ответы: ![]()
![]()
7. Найдите значение выражения:
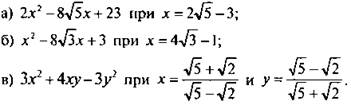
Ответы: а) 1; б) -44; в) ![]()
VII. Подведение итогов урока