Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Решение задач с помощью квадратных уравнений - ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ - КВАДРАТНЫЕ УРАВНЕНИЯ
Цель: применить квадратные уравнения для решения алгебраических и геометрических задач.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Напишите формулу корней квадратного уравнения ax2 + bх + с = 0.
2. Решите уравнение:
а) 9х2 + 24х + 16 = 0;
б) 3x2 – 8x + 7 = 0;
в) 3х2 + 16х - 12 = 0;
г) х2 – х + а - а2 =0;
д) |х2 + 7х + 8| = 8.
Вариант 2
1. Напишите формулу корней квадратного уравнения ах2 + 2kх + с = 0.
2. Решите уравнение:
а) 16х2 + 24x + 9 = 0;
б) 2х2 + 7х - 4 = 0;
в) 4х2 + 11х + 9 = 0;
г) х2 – х – 4a2 – 2a = 0;
д) |х2 + 5х + 6| = 6.
III. Изучение нового материала (основные понятия)
Многие задачи алгебры, геометрии, физики, техники и т. д. приводят к необходимости решения квадратных уравнений.
Пример 1
Произведение двух натуральных чисел, одно из которых на 5 больше другого, равно 104. Найти эти числа.
Пусть меньшее из данных чисел равно х, тогда большее число равно х + 5. По условию произведение этих чисел равно 104, Поэтому получаем уравнение: х(х + 5) = 104 или х2 + 5х - 104 = 0. Решим это квадратное уравнение. Найдем его дискриминант D = 52 – 4 · 1 · (-104) = 441 = 212 корни ![]() т.е.
т.е. ![]() Второй корень по смыслу задачи не подходит, т. к. даны натуральные числа. Итак, меньшее число равно 8, тогда большее число равно 8 + 5 = 13.
Второй корень по смыслу задачи не подходит, т. к. даны натуральные числа. Итак, меньшее число равно 8, тогда большее число равно 8 + 5 = 13.
Ответ: 8 и 13.
Пример 2
В прямоугольном треугольнике один катет больше другого на 7 см, а гипотенуза больше меньшего катета на 8 см. Найти стороны треугольника.
Пусть длина меньшего катета составляет х см, тогда длина большего катета равна х + 7 см, длина гипотенузы равна х + 8 см. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. Получаем уравнение: (х + 8)2 = х2 + (х + 7)2 или х2 + 16х + 64 = х2 + х2 + 14х + 49, или 0 = х2 - 2х - 15. Корни этого квадратного уравнения х1 = 5 и х2 = -3. По смыслу задачи значение х должно быть положительным числом. Поэтому подходит только первый корень х = 5. Тогда длина второго катета равна 5 + 7 = 12 см, длина гипотенузы 5 + 8 = 13 см.
Ответ: 5 см, 12 см, 13 см.
Пример 3
Тело брошено вертикально вверх с начальной скоростью V0 = 50 м/с. Через сколько секунд тело окажется на высоте h. Вычислите для случаев:
a) h = 80 м, б) h = 125 м, в) h = 150 м.
Из физики известно, что высота h (м), на которой брошенное вертикально вверх тело окажется через t секунд, может быть найдена по формуле ![]() Здесь V0 — начальная скорость (м/с), g — ускорение свободного падения, приближенно равное 10 м/с2. Подставим значения V0 и g в формулу и получим уравнение h = 50t – 5t2 или 5t2 – 50t + h = 0. Найдем дискриминант этого квадратного уравнения с параметром h и получим D1 = (-25)2 - 5 · h = 625 – 5h. Для данных значений h найдем корни уравнения.
Здесь V0 — начальная скорость (м/с), g — ускорение свободного падения, приближенно равное 10 м/с2. Подставим значения V0 и g в формулу и получим уравнение h = 50t – 5t2 или 5t2 – 50t + h = 0. Найдем дискриминант этого квадратного уравнения с параметром h и получим D1 = (-25)2 - 5 · h = 625 – 5h. Для данных значений h найдем корни уравнения.
а) Если h = 80 м, то D1 = 625 - 5 · 80 = 225 = 152 и ![]() т. е. t1 = 8 (с) и t2 = 2 (с). В этом случае тело окажется на данной высоте дважды: при подъеме верх (t = 2 с) и при падении вниз (t = 8 с).
т. е. t1 = 8 (с) и t2 = 2 (с). В этом случае тело окажется на данной высоте дважды: при подъеме верх (t = 2 с) и при падении вниз (t = 8 с).
б) Если h = 125 м, то D1 = 625 – 5 · 125 = 0 и t = 25/5 = 5. В этом случае тело окажется на данной высоте однажды через t = 5 с и эта высота — наивысшая высота подъема тела.
в) Если h = 150 м, то D1 = 625 - 5 · 150 = -125. Так как D1 отрицательный, то уравнение решений не имеет. Это означает, что кинетической энергии тела ![]() (где m — масса тела) не хватает для его подъема на заданную высоту h.
(где m — масса тела) не хватает для его подъема на заданную высоту h.
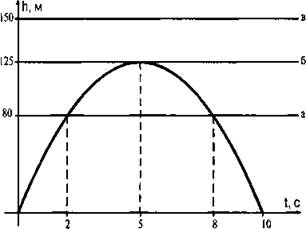
Для наглядности на рисунке приведена зависимость h от t, т. е. h = 50t – 5t2. Из графика видно, что тело в течение первых пяти секунд поднимается до высоты 125 м, а затем в течение следующих пяти секунд падает вниз. Через 10 с после броска тело падает на землю.
На высоте h = 80 м тело оказывается дважды: через 2 с (подъем) и 8 с (падение) от момента броска (случай а). На высоте h = 125 м тело оказывается однажды через 5 с в наивысшей точке подъема (случай б). На высоте h = 150 м тело оказаться не может (случай в).
Из приведенного примера также видно, что в зависимости от значения параметра h квадратное уравнение 5t2 - 50t + h = 0 имеет различные решения. Этим решениям соответствует различная физическая ситуация.
IV. Задание на уроке
№ 556, 558, 563, 656, 566,568.
V. Задание на дом
№ 557, 559, 561, 562, 564, 567.
VI. Подведение итогов