Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Решение систем нелинейных неравенств - НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ - НЕРАВЕНСТВА
Цель: рассмотреть решение некоторых типов систем линейных и нелинейных неравенств с олной и двумя переменными.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (тест).
Вариант 1
1. Решите систему неравенств ![]()
Ответы: а) (1,6; 4); б) (-∞; 1,6); в) (4; +∞).
2. Решите двойное неравенство ![]()
Ответы: а) (-∞; 1]; б) [3; +∞); в) (-1; 3].
3. Найдите допустимые значения переменной для выражения ![]()
Ответы: а) (1/2; +∞); б) (1/2; 5/3]; в) х ≠ 1/2.
Вариант 2
1. Решите систему неравенств ![]()
Ответы: а) (18/7; +∞); б) (1; +∞); в) (1; 18/7).
2. Решите двойное неравенство ![]()
Ответы: а) (-1; +∞]; б) (-∞; 17/3]; в) (-1; 17/3].
3. Найдите допустимые значения переменной для выражения ![]()
Ответы: а) х ≠ 7/3; б) (7/3; +∞); в) [5/3; +∞).
III. Изучение нового материала (основные понятия)
Во многих случаях приходится решать как системы линейных неравенств, так и системы нелинейных неравенств. К подобных системам приводит решение неравенств с модулями. При этом полезно помнить, что
а) неравенство |х| ≤ а (по свойству модуля) равносильно двойному неравенству –a ≤ x ≤ a;
б) неравенство [х| ≥ a равносильно двум неравенствам (или совокупности неравенств) х ≤ -а и х ≥ а.
Подчеркнем, что речь идет именно о совокупности, а не системе неравенств.
Пример 1
Решим неравенство |1 - 5х| ≤ 2.
Такое неравенство равносильно двойному неравенству: -2 ≤ 1 – 5x ≤ 2. Решим его обычным способом. Получаем: -2 – 1 ≤ -5х ≤ 2 - 1 или -3 ≤ -5х ≤ 1, откуда 3/5 ≥ х ≥ -1/5. Таким образом, решение данного неравенства х ∈ [-1/5; 3/5].
Пример 2
Решим неравенство |3х - 2| ≥ 4.
Данное неравенство равносильно совокупности неравенств (именно совокупности, а не системе): ![]() Решим каждое неравенство такой совокупности. Имеем:
Решим каждое неравенство такой совокупности. Имеем: ![]() или
или ![]() откуда
откуда 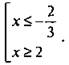 Решение такой совокупности и данного неравенства х ∈ (-∞; -2/3]U[2; +∞).
Решение такой совокупности и данного неравенства х ∈ (-∞; -2/3]U[2; +∞).
Заметим, что решением совокупности неравенств является (в отличие от системы неравенств) такое значение переменной, при котором выполняется хотя бы одно из неравенств. Поэтому, чтобы найти решение совокупности неравенств (в отличие от системы неравенств), надо найти объединение множеств решений всех неравенств совокупности.
Часто к решению систем неравенств приводит исследование корней квадратного уравнения.
Пример 3
При каких значениях параметра а оба корня уравнения ![]() принадлежат промежутку [-3; 3]?
принадлежат промежутку [-3; 3]?
Прежде всего найдем дискриминант данного квадратного уравнения ![]()
![]() и решим его
и решим его ![]() т. е. x1 = a - 1 и х2 = 3 – 2a. Теперь потребуем, чтобы эти корни принадлежали промежутку [-3; 3]. Получаем систему линейных неравенств:
т. е. x1 = a - 1 и х2 = 3 – 2a. Теперь потребуем, чтобы эти корни принадлежали промежутку [-3; 3]. Получаем систему линейных неравенств: ![]() Решим эту систему. Имеем:
Решим эту систему. Имеем: ![]() или
или ![]() Решение такой системы — промежуток [0; 3]. Кроме того, надо учесть, что уравнение может иметь не два, а один корень. В этом случае D = 0, т. е. 3а - 4 = 0, откуда а = 4/3. Итак, при
Решение такой системы — промежуток [0; 3]. Кроме того, надо учесть, что уравнение может иметь не два, а один корень. В этом случае D = 0, т. е. 3а - 4 = 0, откуда а = 4/3. Итак, при ![]() оба корня данного квадратного уравнения принадлежат промежутку [-3; 3].
оба корня данного квадратного уравнения принадлежат промежутку [-3; 3].
Пример 4
Рассмотрим уравнение предыдущего примера и потребуем, чтобы хотя бы один из корней принадлежал промежутку [-3; 3]. В этом случае вместо системы неравенств получим аналогичную совокупность неравенств ![]() Решив каждое неравенство, найдем
Решив каждое неравенство, найдем 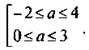 Решение этой совокупности — промежуток [-2; 4].
Решение этой совокупности — промежуток [-2; 4].
Итак, при а ∈ [-2; 4] хотя бы один из корней данного квадратного уравнения принадлежит промежутку [-3; 3].
Пример 5
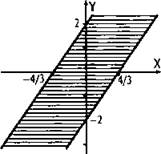
На координатной плоскости изобразим множество точек, координаты которых удовлетворяют неравенству |3х – 2y| ≤ 4.
Используя свойство модуля, запишем данное неравенство в виде двойного неравенства -4 ≤ 3х - 2у ≤ 4 и выразим из него у. Получаем: ![]() откуда
откуда ![]() Сначала построим две граничные линии
Сначала построим две граничные линии ![]() Они представляют собой две параллельные прямые. Эти прямые разбивают точки координатной плоскости на область, расположенную между ними, и область, расположенную за ними. Проверка показывает, что данному неравенству удовлетворяют точки, расположенные между прямыми (эти точки заштрихованы). Например, для начала координат (контрольная точках x = 0, у = 0) получаем, что данное неравенство |3x - 2у| ≤ 4 выполняется |3 · 0 – 2 · 0) ≤ 4.
Они представляют собой две параллельные прямые. Эти прямые разбивают точки координатной плоскости на область, расположенную между ними, и область, расположенную за ними. Проверка показывает, что данному неравенству удовлетворяют точки, расположенные между прямыми (эти точки заштрихованы). Например, для начала координат (контрольная точках x = 0, у = 0) получаем, что данное неравенство |3x - 2у| ≤ 4 выполняется |3 · 0 – 2 · 0) ≤ 4.
Пример 6
На координатной плоскости изобразим множество точек, координаты которых удовлетворяют уравнению mах(3x – y; х + у) = 2.
Прежде всего, заметим, что запись mах(a; b) означает наибольшую (максимальную) из двух величин а и b. Для данного примера неизвестно, какая из величин 3х - у и х + у больше. Поэтому необходимо рассмотреть два возникающих случая.
1) 3х – у ≥ х + у (т. е. первая величина является наибольшей). По условию задачи тогда 3х - у = 2. Таким образом, первый случай сводится к системе, состоящей из неравенства и уравнения ![]() или
или 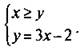
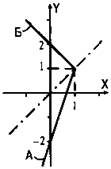
Построим прямую х = у (штрих — пунктирная линия). Она разбивает все точки координатной плоскости на области 1 и 2. Легко проверить, что неравенству х ≥ у отвечают точки области 1. В этой области построим прямую у = 3х - 2 (луч А). Таким образом, данному случаю (данной системе) соответствует луч А.
2) х + у > 3х - у (т. е. вторая величина является наибольшей). По условию задачи тогда х + у = 2. Таким образом, второй случай также сводится к системе, состоящей из неравенства и уравнения ![]() или
или ![]() Неравенству у > х отвечают точки области 2. В этой области построим прямую у = 2 - х (луч Б). Таким образом, данному случаю (данной системе) соответствует луч Б.
Неравенству у > х отвечают точки области 2. В этой области построим прямую у = 2 - х (луч Б). Таким образом, данному случаю (данной системе) соответствует луч Б.
Итак, фафиком уравнения mах(3х - y; х + у) = 2 являются лучи А и Б. Теперь усложним рассмотренную задачу и разберем следующий пример.
Пример 7
На координатной плоскости изобразим множество точек, координаты которых удовлетворяют неравенству mах(3x - у; x + y) > 2.
Подход к этой задаче аналогичен предыдущему. Также возникают два случая, каждый из которых приводит к системе, состоящей из двух неравенств.
1) В этом случае возникает система двух неравенств ![]() или
или ![]()
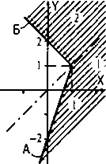
Отличие от предыдущего примера состоит в том, что второе условие становится неравенством. Поэтому в области 1 строим множество точек, отвечающих неравенству у < 3х - 2. Эти точки расположены ниже луча А (точки заштрихованы, стрелки указывают, что неравенство строгое и граничные точки не входят).
2) В этом случае возникает также система двух неравенств ![]() или
или ![]() Вновь отличие от предыдущего примера состоит в том, что второе условие становится неравенством. Поэтому в области 2 строим множество точек, отвечающих неравенству у > 2 - х. Эти точки расположены выше луча Б (точки заштрихованы, стрелки указывают, что неравенство строгое и граничные точки не входят).
Вновь отличие от предыдущего примера состоит в том, что второе условие становится неравенством. Поэтому в области 2 строим множество точек, отвечающих неравенству у > 2 - х. Эти точки расположены выше луча Б (точки заштрихованы, стрелки указывают, что неравенство строгое и граничные точки не входят).
Итак, графиком неравенства mах(3x - у; x + y) > 2 является множество заштрихованных точек.
Рассмотрим теперь графическое решение других нелинейных систем неравенств.
Пример 8
На координатной плоскости изобразим множество точек, координаты которых удовлетворяют системе неравенств ![]()
Преобразуем сначала первое неравенство, выделив полные квадраты суммы и разности по переменным х и у. Получаем: ![]() или
или ![]() или
или ![]() Будем рассматривать теперь систему неравенств
Будем рассматривать теперь систему неравенств 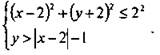
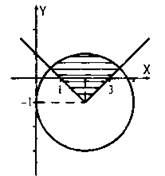
Сначала построим график уравнения ![]() Это окружность с центром в точке А (2; -1) радиуса 2. Легко проверить, что неравенству
Это окружность с центром в точке А (2; -1) радиуса 2. Легко проверить, что неравенству ![]() соответствуют точки внутри и на границе построенной окружности (т. е. точки круга).
соответствуют точки внутри и на границе построенной окружности (т. е. точки круга).
Теперь построим график функции y = |х - 2| - 1. Он получается из графика y = |x| смещением на две единицы вправо и одну единицу вниз («галочка»). Неравенству y > |х - 2| - 1 отвечают точки, распложенные внутри ветвей этого графика. При этом точки, лежащие на ветвях графика, не входят (что показано стрелочками), т. к. неравенство строгое.
Таким образом, графиком данной системы неравенств являются точки кругового сектора (они заштрихованы). При этом точки, лежащие на граничных радиусах, в график не входят.
IV. Задание на уроке и дома
1. Решите неравенства:
![]()
Ответы: 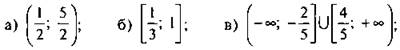
![]() .
.
2. При каких значениях параметра a
а) оба корня уравнения ![]() принадлежат промежутку [-1; 2];
принадлежат промежутку [-1; 2];
б) хотя бы один корень данного уравнения принадлежит промежутку [-1; 2|;
в) только один корень этого уравнения принадлежит промежутку [-1; 2];
г) оба корня такого уравнения положительны;
д) корни отличаются в два раза?
Ответы: ![]()
![]()
3. На координатной плоскости изобразить множество точек, координаты которых удовлетворяют условию:
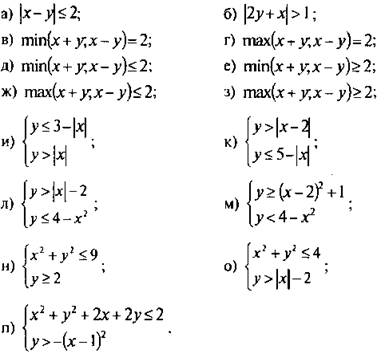
V. Подведение итогов урока