Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Умножение дробей. Возведение дроби в степень - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ
Целы изучить умножение дробей и возведение их в степень.
Ход урока
I. Сообщение темы и цели урока .
II. Изучение нового материала (основные понятия)
При умножении обыкновенных дробей получается дробь, числитель которой равен произведению числителей дробей, а знаменатель — произведению знаменателей. Например ![]() По тому же правилу находят и произведения рациональных дробей, т. е.
По тому же правилу находят и произведения рациональных дробей, т. е. ![]() при любых допустимых значениях переменных (т. е. при b ≠ 0 и d ≠ 0). Докажем это равенство.
при любых допустимых значениях переменных (т. е. при b ≠ 0 и d ≠ 0). Докажем это равенство.
Пусть ![]() (очевидно, что b ≠ 0 и d ≠ 0). Почленно умножим эти равенства и получим
(очевидно, что b ≠ 0 и d ≠ 0). Почленно умножим эти равенства и получим ![]() . Из равенства a/b = m по определению частного имеем а = bm, из равенства c/d = n получаем с = dn. Также почленно умножим равенства а = bm и с = dn и получим
. Из равенства a/b = m по определению частного имеем а = bm, из равенства c/d = n получаем с = dn. Также почленно умножим равенства а = bm и с = dn и получим ![]() Выразим из этого равенства mn = ac/bd. Сравнивая два равенства
Выразим из этого равенства mn = ac/bd. Сравнивая два равенства ![]() и
и ![]() имеем тождество
имеем тождество ![]() (при b ≠ 0 и d ≠ 0), из которого следует правило умножения дробей. Чтобы умножить дробь на дробь, надо перемножить их числители и перемножить их знаменатели. Первое произведение записать числителем, второе — знаменателем дроби.
(при b ≠ 0 и d ≠ 0), из которого следует правило умножения дробей. Чтобы умножить дробь на дробь, надо перемножить их числители и перемножить их знаменатели. Первое произведение записать числителем, второе — знаменателем дроби.
Пример 1
Умножим дроби ![]()
Используя правило умножения дробей, получаем: ![]()
![]()
Пример 2
Умножим дроби ![]()
Воспользуемся правилом умножения дробей. Затем числитель первой дроби и знаменатель второй дроби разложим на множители и сократим получившуюся дробь. Имеем: ![]()
![]()
Пример 3
Представим произведение дробей ![]() в виде рациональной дроби.
в виде рациональной дроби.
Используем правило умножения дробей. В числителе и знаменателе получившейся дроби умножим многочлены. Тогда получим: ![]()
Пример 4
Умножим дробь ![]() и многочлен х2 – у2.
и многочлен х2 – у2.
Как и при сложении (вычитании) дробей, представим многочлен в виде дроби со знаменателем 1 и воспользуемся правилом умножения дробей.
Имеем: ![]()
![]()
Правило умножения дробей, разумеется, справедливо для произведения любого числа перемножаемых дробей.
Пример 5
Найдем произведение дробей ![]()
Используем правило умножения дробей и получим: ![]()
![]()
Теперь рассмотрим возведение дроби в степень. При возведении обыкновенной дроби в степень ее числитель и знаменатель возводят в эту степень. Например: 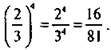 Такое же правило справедливо и в случае рациональной дроби:
Такое же правило справедливо и в случае рациональной дроби: 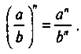 Докажем это.
Докажем это.
По определению степени имеем 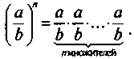 Используем правило умножения дробей и определение степени, получим:
Используем правило умножения дробей и определение степени, получим: 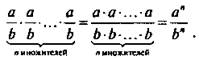 Итак,
Итак, 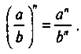 Из доказанного тождества следует правило возведения дроби в степень. Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель дроби и первый результат записать в числителе, второй — в знаменателе дроби.
Из доказанного тождества следует правило возведения дроби в степень. Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель дроби и первый результат записать в числителе, второй — в знаменателе дроби.
Пример 6
Возведем дробь ![]() в четвертую степень.
в четвертую степень.
Используем правило возведения дроби в степень и учтем свойства степеней. Получаем: 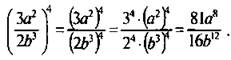
Пример 7
Возведем в квадрат дробь ![]()
Используем формулы сокращенного умножения и сначала сократим дробь: ![]() Теперь возведем в квадрат эту дробь. Для этого возведем в квадрат ее числитель и знаменатель (правило возведения дроби в степень). Получаем:
Теперь возведем в квадрат эту дробь. Для этого возведем в квадрат ее числитель и знаменатель (правило возведения дроби в степень). Получаем: ![]()
III. Контрольные вопросы
1. Сформулируйте правило умножения дробей.
2. Докажите правило умножения дробей.
3. Как возвести дробь в степень?
4. Докажите правило возведения дроби в степень.
IV. Задание на уроке
№ 108 (а, г); 109 (а); 111 (б); 112 (в); 114 (а); 115 (а); 117 (а, д); 118 (а, д); 119 (а, б); 121 (а); 122 (б); 125 (б, г).
V. Задание на дом
№ 108 (e); 110 (в); 111 (а); 112(6); 113 (г); 114 (б); 115 (г); 117 (в); 118 (г); 119 (в, г); 121 (6); 123 (а); 124 (г); 126 (а, в).
VI. Подведение итого урока