Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Понятие квадратичной функции и некоторые ее свойства - ОПРЕДЕЛЕНИЕ КВАДРАТИЧНОЙ ФУНКЦИИ - КВАДРАТИЧНАЯ ФУНКЦИЯ
Цель: рассмотрение квадратичной функции и некоторых ее свойств.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала (основные понятия)
В науке и технике рассматриваются различные функциональные зависимости (функции), описывающие те или иные закономерности природы. Поэтому в алгебре изучаются различные виды функций и их свойства. В 7-м классе вы уже познакомились с линейной функцией у = kх + b, ее свойствами и графиком. Эту функцию можно считать одной из простейших. Рассмотрим теперь более сложную функцию, которая называется квадратичной.
Функция у = ах2 + bх + с (где а, b, с — некоторые числа, причем а ≠ 0; х — переменная (или аргумент» называется квадратичной. Отличительная особенность такой функции — наличие слагаемого, содержащего х2 (и не выше этой степени).
Пример 1
а) Функции ![]() являются квадратичными, т. к. каждая такая зависимость содержит слагаемое, пропорциональное х2.
являются квадратичными, т. к. каждая такая зависимость содержит слагаемое, пропорциональное х2.
б) Функции ![]() не являются квадратичными. Первая функция содержит слагаемое 2х3 более высокой степени, чем слагаемое 3х2. Такая функция называется кубической. Вторая и третья функции помимо слагаемых -5х2 и 7х2 содержат дроби 2/x и
не являются квадратичными. Первая функция содержит слагаемое 2х3 более высокой степени, чем слагаемое 3х2. Такая функция называется кубической. Вторая и третья функции помимо слагаемых -5х2 и 7х2 содержат дроби 2/x и ![]() соответственно. Эти функции специального названия не имеют (хотя могут быть приведены к рациональным функциям).
соответственно. Эти функции специального названия не имеют (хотя могут быть приведены к рациональным функциям).
К квадратичным функциям приводят многие задачи математики и физики.
Пример 2
а) Площадь круга S радиуса R является квадратичной функцией S = πR2 (где π — число, π ≈ 3,14), для которой а = π, b = 0, с = 0.
б) Площадь прямоугольного равнобедренного треугольника S с катетом m является квадратичной функцией S = 1/2m2, для которой a = 1/2, b = 0, с = 0.
в) Кинетическая энергия E тела массы m, движущегося со скоростью V, является квадратичной функцией Е = 1/2mV2, для которой a = 1/2m, b = 0, с = 0.
г) Расстояние S от земли тела, брошенного вверх со скоростью V, в момент времени t является квадратичной функцией ![]() (где g - ускорение свободного падения (постоянная величина), S0 — расстояние от тела до земли в начальный момент времени t = 0), для которой а = -g/2, b = V, c = S0.
(где g - ускорение свободного падения (постоянная величина), S0 — расстояние от тела до земли в начальный момент времени t = 0), для которой а = -g/2, b = V, c = S0.
Как и для любой функции, чтобы найти значение квадратичной функции у(m), надо подставить значение аргумента х = m в аналитический вид функции.
Пример 3
Найдем значения функции у(х) = 2х2 - 3х + 1 при х = -3, х = 0, х = 2, х = m, х = -2m.
Подставив соответствующие значения аргумента, получим.
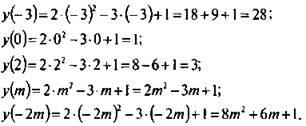
Часто встречается и обратная задача: по известному значению функции у = n найти значение аргумента, для которого оно достигается. Для этого в аналитический вид функции y(x) надо подставить значение функции у = n и решить полученное уравнение n = у(х). В частности, для квадратичной функции у(х) = ах2 + bх + с получим квадратное уравнение n = ах2 + bх + с.
Пример 4
Найдем, при каких значениях аргумента х квадратичная функция y = x2 - 2x - 8 принимает значение, равное а) -11, б) -9, в) 7, г) 0.
Подставив соответствующее значение функции п в аналитический вид функции y = x2 - 2x - 8, получим уравнение:
а) -11 = х2 - 2х - 8 или 0 = х2 - 2х + 3. Дискриминант этого квадратного уравнения D = (-2)2 – 4 · 1 · 3 = -8 < 0, и оно действительных корней не имеет. Поэтому данная функция значения у = -11 не принимает ни при каких действительных значениях аргумента х.
б) -9 = х2 - 2х - 8, или 0 = х2 - 2х + 1, или 0 = (x – 1)2. Единственный корень этого уравнения x = 1. Следовательно, данная функция принимает значение y = -9 только при одном значении аргумента.
в) 7 = х2 - 2х - 8 или 0 = х2 - 2х - 15. Корни такого квадратного уравнения ![]() т. е. х1 = 5 и х2 = -3. Поэтому значение y = 7 функция принимает при двух значениях аргумента х1 = 5 и х2 = -3, т. е. y(5) = 7 и y(-3) = 7.
т. е. х1 = 5 и х2 = -3. Поэтому значение y = 7 функция принимает при двух значениях аргумента х1 = 5 и х2 = -3, т. е. y(5) = 7 и y(-3) = 7.
г) 0 = х2 - 2х - 8. Корни этого квадратного уравнения ![]()
![]() т. е. х1 = 4 и х2 = -2. Следовательно, значение у = 0 функция принимает для двух значений аргумента х1 = 4 и х2 = -2.
т. е. х1 = 4 и х2 = -2. Следовательно, значение у = 0 функция принимает для двух значений аргумента х1 = 4 и х2 = -2.
Напомним, что значения аргумента, для которых значение функции равно нулю, называются нулями функции. В частности, нулями квадратичной функции y = x2 - 2x - 8 являются значения аргумента х1 = 4 и х2 = -2.
Пример 5
Найдем нули функции: ![]()
а) Положим значение функции у = 0 и получим квадратное уравнение 0 = 3х2 - 7х + 2. Корни этого квадратного уравнения ![]() т. е.
т. е. ![]() Поэтому данная функция имеет нули: х1 = 2 и х2 = 1/3.
Поэтому данная функция имеет нули: х1 = 2 и х2 = 1/3.
б) Положим значение функции у = 0 и получим рациональное уравнение ![]() Такая дробь равна нулю, если ее числитель равен нулю, а знаменатель в нуль не обращается. Получаем систему
Такая дробь равна нулю, если ее числитель равен нулю, а знаменатель в нуль не обращается. Получаем систему ![]() Корни квадратного уравнения 0 = 2х2 – х - 1 равны
Корни квадратного уравнения 0 = 2х2 – х - 1 равны ![]() т. е. х1 = 1 и х2 = 1/2. Однако значение х = 1 не удовлетворяет неравенству х - 1 ≠ 0. Поэтому данная функция имеет только один нуль х = -1/2.
т. е. х1 = 1 и х2 = 1/2. Однако значение х = 1 не удовлетворяет неравенству х - 1 ≠ 0. Поэтому данная функция имеет только один нуль х = -1/2.
Пример 6
Найдем нули функции у = 5х2 - 6ax + a2 (где a — некоторое число).
Положим значение функции у = 0 и получим квадратное однородное уравнение 0 = 5х2 – 6aх + a. Найдем его корни ![]()
![]() т. е. х1 = а и х2 = a/5 . Следовательно, при а ≠ 0 нули данной функции x1 = а и х2 = a/5; при а = 0 нуль данной функции х = 0.
т. е. х1 = а и х2 = a/5 . Следовательно, при а ≠ 0 нули данной функции x1 = а и х2 = a/5; при а = 0 нуль данной функции х = 0.
Рассмотрим более сложные задачи, связанные с квадратичной функцией.
Пример 7
Известны три значения квадратичной функции ![]()
![]() Найдем числа а, b и с.
Найдем числа а, b и с.
Запишем значения функции при значениях аргумента х = -2, х = 0 и х = 3. Получим систему трех линейных уравнений с тремя неизвестными: 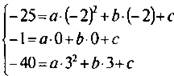 или
или 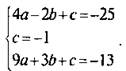 Подставим значение с = -1 в первое и третье уравнения и получим систему двух уравнений с двумя неизвестными:
Подставим значение с = -1 в первое и третье уравнения и получим систему двух уравнений с двумя неизвестными: ![]() или
или ![]() Сложим уравнения системы и получим 5а = -25, откуда а = -5. Подставим это значение в первое уравнение системы: 2 · (-5) - b = -12 или 10 + b = 12, откуда b = 2. Итак, а = -5, b = 2 и с = -1.
Сложим уравнения системы и получим 5а = -25, откуда а = -5. Подставим это значение в первое уравнение системы: 2 · (-5) - b = -12 или 10 + b = 12, откуда b = 2. Итак, а = -5, b = 2 и с = -1.
Пример 8
Один из нулей функции ![]() равен 6. Найдем другой нуль этой функции.
равен 6. Найдем другой нуль этой функции.
Рассмотрим два способа решения такой задачи.
1 способ. Нули данной квадратичной функции определяются квадратным уравнением ![]() Найдем его корни:
Найдем его корни: ![]() т. е. х1 = 3а и х2 = 1 – 2a. Теперь рассмотрим два случая:
т. е. х1 = 3а и х2 = 1 – 2a. Теперь рассмотрим два случая:
а) пусть первый нуль равен 6 (т. е. 3а = 6), откуда а = 2. Тогда второй нуль данной функции х2 = 1 - 2а = 1 – 2 · 2 = -3;
б) пусть второй нуль равен 6 (т. е. 1 - 2а = 6), откуда a = -5/2. Тогда первый нуль данной функции ![]()
2 способ. Так как один из нулей данной функции равен 6, то подставим это значение в уравнение 0 = х2 - (а + 1)х - 6а2 + 3а и получим: ![]() или 2a2 + а - 10 = 0. Корни этого уравнения
или 2a2 + а - 10 = 0. Корни этого уравнения ![]() т. е. a1 = -5/2 и а2 = 2. Теперь исследуем квадратное уравнение
т. е. a1 = -5/2 и а2 = 2. Теперь исследуем квадратное уравнение ![]() Возникают два случая:
Возникают два случая:
а) для а = -5/2 это уравнение имеет вид: ![]() или 0 = 2х + 3х - 90. Корни этого уравнения
или 0 = 2х + 3х - 90. Корни этого уравнения ![]() т. е. х1 = 6 и х2 = –15/2.
т. е. х1 = 6 и х2 = –15/2.
б) для а = 0 уравнение имеет вид: 0 = х2 - 3х - 18. Корни такого уравнения ![]() т. е. х1 = -3 и х2 = 6.
т. е. х1 = -3 и х2 = 6.
Итак, при a = -5/2 другой нуль данной функции х = -15/2; при а = 2 другой нуль функции х = -3; при других а задача не имеет решений.
Пример 9
Для квадратичной функции у(х) выполнено условие ![]() Найдем данную функцию y(х).
Найдем данную функцию y(х).
Заметим, что запись у(х + 2) означает значение функции y(x) при значении аргумента х + 2. Рассмотрим два способа решения этой задачи.
1 способ. Квадратичная функция у(х) имеет вид у(х) = ах2 + bх + с. Тогда ![]()
![]() Сравним это значение с данным значением
Сравним это значение с данным значением ![]() Приравнивая коэффициенты при соответствующих степенях х, получим систему трех линейных уравнений с тремя неизвестными:
Приравнивая коэффициенты при соответствующих степенях х, получим систему трех линейных уравнений с тремя неизвестными: 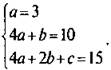 Подставим значение а = 3 во второе и третье уравнения системы. Имеем систему двух линейных уравнений с двумя неизвестными:
Подставим значение а = 3 во второе и третье уравнения системы. Имеем систему двух линейных уравнений с двумя неизвестными: ![]() Из первого уравнения этой системы найдем b = -2. Тогда из второго уравнения имеем: 12 + 2 · (-2) + с = 15, откуда с = 7. Итак, получили а = 3, b = -2, с = 7 и функция у(х)= 3х2 - 2х + 7.
Из первого уравнения этой системы найдем b = -2. Тогда из второго уравнения имеем: 12 + 2 · (-2) + с = 15, откуда с = 7. Итак, получили а = 3, b = -2, с = 7 и функция у(х)= 3х2 - 2х + 7.
2 способ. Так как дано ![]() то обозначим буквой t = х + 2. Тогда х = t - 2. Подставим эту величину в равенство у(х + 2) = 3х2 + 10х + 15 и получим
то обозначим буквой t = х + 2. Тогда х = t - 2. Подставим эту величину в равенство у(х + 2) = 3х2 + 10х + 15 и получим ![]() Имеем y(t) = 3t2 – 2t + 7. Так как аргумент функции можно обозначить любой буквой х, t, z и т. д., то сразу получаем у(х) = 3х2 - 2х + 7.
Имеем y(t) = 3t2 – 2t + 7. Так как аргумент функции можно обозначить любой буквой х, t, z и т. д., то сразу получаем у(х) = 3х2 - 2х + 7.
Заметим, что второй способ решения универсальный, т. к. изначально не требуется, чтобы y(x) была квадратичной.
Пример 10
Для квадратичной функции у(х) выполнено условие ![]() Найдем данную функцию у(х).
Найдем данную функцию у(х).
Запись y(-х) означает значение функции у(х) при значении аргумента (-х). Для решения этой задачи также можно использовать два способа, подобные примененным в примере 9.
1 способ. Квадратичная функция у(х) имеет вид y(x) = ax2 + bх + с. Тогда ![]() Найдем выражение
Найдем выражение ![]()
![]() Сравнивая это выражение с данным равенством
Сравнивая это выражение с данным равенством ![]() получаем систему трех уравнений с тремя неизвестными
получаем систему трех уравнений с тремя неизвестными 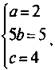 откуда a = 2, b = -1, с = 4. Тогда данная функция у(х) = 2х2 – х + 4.
откуда a = 2, b = -1, с = 4. Тогда данная функция у(х) = 2х2 – х + 4.
2 способ. Данное равенство ![]() запишем для значения аргумента (-х) и получим:
запишем для значения аргумента (-х) и получим: ![]()
![]() Для удобства обозначим а = у(х) и b = у(-х). Для неизвестных а и b имеем систему двух линейных уравнений:
Для удобства обозначим а = у(х) и b = у(-х). Для неизвестных а и b имеем систему двух линейных уравнений: ![]() В этой системе нас интересует только неизвестная а. Поэтому используем способ сложения. Умножим первое уравнение на число 3, второе уравнение — на число 2:
В этой системе нас интересует только неизвестная а. Поэтому используем способ сложения. Умножим первое уравнение на число 3, второе уравнение — на число 2: 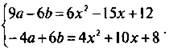 Сложим уравнения системы и получим 5a = 10х2 - 5х + 20, откуда a = 2х2 – х + 4, т. е. у(х) = 2х2 – х + 4.
Сложим уравнения системы и получим 5a = 10х2 - 5х + 20, откуда a = 2х2 – х + 4, т. е. у(х) = 2х2 – х + 4.
Вновь второй способ оказался универсальным, т. к. не требуется, чтобы функция у(х) была квадратичной.
III. Контрольные вопросы
1. Приведите примеры квадратичных функций.
2. Какая функция называется квадратичной?
3. Какие значения аргумента называются нулями функции?
IV. Задание на уроке
№ 578 (1, 3,5); 579 (2); 581 (1); 582 (1, 5); 583 (2); 585 (1, 3).
V. Задание на дом
№ 578 (2,4, 6); 579 (4); 581 (4); 582 (2, 6); 583 (4); 585 (2, 4).
VI. Творческие задания
1. Дана квадратичная функция у(х) = -х2 + 7х + 4. Найти:
![]()
2. Дана квадратичная функция у = 2х2 - 5х + 8. Найти:
![]()
3. Для квадратичной функции y(x) = ax2 + bх + с известны некоторые значения. Найти коэффициенты а, b и с:
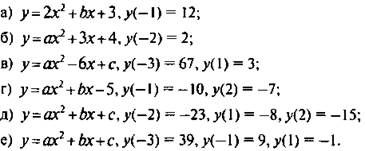
Ответы: а) а = 2, b = -7, с = 3; б) а = -2, b = -3, с = 4; в) а = 5, b = -6, с = 4; г) a = -2, b = 3, с = -5; д) а = -3, b = 2, с = -7; е) а = 2, b = -6, с = 3.
4. Найти нули функции:
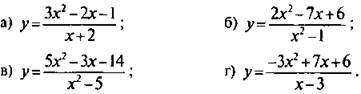
Ответы: ![]()
5. Найти нули функции:
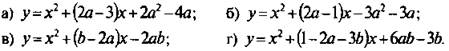
Ответы: а) при а ≠ - 2 х1 = 2а и х2 = а - 2, при а = -2 х = -4;
б) при а ≠ -1/4 х1 = 3а и х2 = a + 1, при а = -1/4 х = 3/4;
в) х1 = 2a и х2 = -b.
г) х1 = 2а – 1 и х2 = 3b.
6. Один из нулей функции y(x) известен. Найти другой нуль функции:
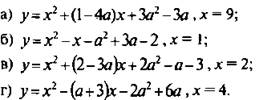
Ответы: а) при а = 3 х = 2, при а = 10 х = 30;
б) при a = 2 х = 0, при a = 1 х = 0;
в) при a = 1 х = -1, при a = 5/2 x = 7/2;
г) при a = -1 х = -2, при a = 2 х = 1.
7. Найти квадратичную функцию y(х), если выполнено условие:
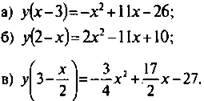
Ответы: ![]()
8. Найти квадратичную функцию ,у(х), если выполнено условие:
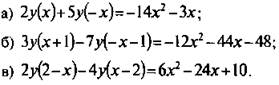
Ответы: ![]()
VII. Подведение итогов урока