Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Изучение функции ах2, построение ее графика - ФУНКЦИЯ у = ах2 - КВАДРАТИЧНАЯ ФУНКЦИЯ
Цель: рассмотреть более сложную квадратичную функцию у = ах2 изучить ее свойства и построить график.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Определить, какие точки принадлежат графику функции у = х2: ![]()
2. Найти координаты точек пересечения параболы у = х2 и прямой y = -2х + 3.
3. Возрастает или убывает функция у = х2 на промежутке [-4; -1)?
Вариант 2
1. Определить, какие точки принадлежат графику функции у = х2: ![]()
2. Найти координаты точек пересечения параболы у = х2 и прямой у = -3х + 4.
3. Возрастает или убывает функция у = х2 на промежутке (-5; -2]?
III. Изучение нового материала (основные понятия)
Рассмотрим более сложную (по сравнению с предыдущим уроком) квадратичную функцию у = ах2. Прежде всего необходимо понять, каким образом влияет на график функции модуль и знак коэффициента а. Сначала обсудим влияние модуля коэффициента а, рассмотрев, например, положительные значения а.
Пример 1
Построим в одних осях координат графики функций у = х2, у = 2х2 и y = 1/2x2 и сравним их. Составим таблицу значений для этих функций в промежутке [-2; 2] с шагом 0,5.
x |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
y = х2 |
4 |
2,25 |
1 |
0,25 |
0 |
0,25 |
1 |
2,25 |
4 |
у = 2х2 |
8 |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
8 |
y = 1/2x2 |
2 |
1,12 |
0,5 |
0,12 |
0 |
0,12 |
0,5 |
1,12 |
2 |
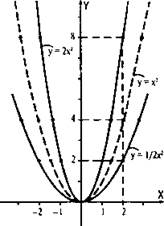
Сначала сравним графики функций у = 2х2 и у = х2. Как видно из таблицы и из графиков, при одном и том же значении х значение функции у = 2х2 в 2 раза больше значения функции у = х2. Это означает, что каждую точку графика у = 2х2 можно получить из точки графика у = х2 с той же абсциссой увеличением ее ординаты в 2 раза.
Говорят, что график функции у = 2х2 получается растяжением графика функции у = х2 вдоль оси Оу в 2 раза (от оси Ох).
Теперь сравним графики функций y = 1/2x2 и у = х2. Видно, что при одном и том же значении х значение функции y = 1/2x2 в 2 раза меньше значения функции у = х2. Таким образом, каждую точку графика y = 1/2x2 можно получить из точки графика у = х2 с той же абсциссой уменьшением ее ординаты в 2 раза. Говорят, что график функции y = 1/2x2 получается сжатием графика функции у = х2 вдоль оси Оу в 2 раза (к оси Ох).
Остановимся на влиянии знака коэффициента а на график функции.
Пример 2
Построим в одних осях координат графики функций у = х2 и у = -х2.
Сравним функции у = х2 и у = -х2. При одном и том же значении х значения этих функций равны по модулю и противоположны по знаку. Поэтому график функции у = -х2 можно получить симметрией (отражением) относительно оси Ох графика функции у = х2.
Аналогично, графики функций у = -2х2 и y = -1/2x2, соответственно, симметричны относительно оси Ох графикам функций у = 2х2 и y = 1/2x2, построенным на предыдущем рисунке.
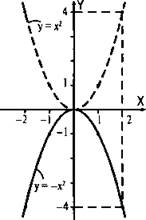
График функции у = ах2 при любом а ≠ 0 также называют параболой. При а > 0 ветви параболы направлены вверх, а при а < 0 — вниз.
Отметим, что фокус параболы у = ах2 находится в точке F(0; 1/4a).
Укажем основные свойства функции у = ах2 (для а ≠ 0).
1. Область определения функции - все действительные значения х.
2. Область изменения (значений) функции - при а > 0 все у ≥ 0 и при а < 0 все у ≤ 0.
3. При а > 0 функция принимает положительные значения для х ≠ 0, при а < 0 функция принимает отрицательные значения для х ≠ 0. Значение функции у = 0 только при х = 0.
4. Парабола у = ах2 симметрична относительно оси ординат. Вершиной параболы является начало координат, г. е. точка (0; 0). Функция у = ах2 является четной.
5. При а > 0 функция возрастает при х ≥ 0 и убывает при x ≤ 0. При а < 0 функция возрастает при x ≤ 0 и убывает при x ≥ 0.
Все перечисленные свойства видны из представленных графиков.
Рассмотрим типичные задачи по этой теме.
Пример 3
Решим графически: а) уравнение -х2 = -4; б) неравенство -х2 ≤ -4; в) уравнение -x2 = -2; г) неравенство -х2 > -2.
Сначала построим график функции у = -х2 (парабола).
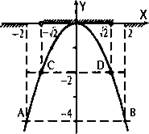
а) Проведем прямую у = -4 (горизонтальная прямая). Видно, что парабола и прямая пересекаются в точках А и В, абсциссы которых, соответственно, х = -2 и х = 2. Следовательно, уравнение –х2 = -4 имеет два корня х1 = -2 и х2 = 2.
б) Графический смысл неравенства -х2 ≤ -4: надо найти такие значения х, при которых точки параболы лежат не выше (ниже или на уровне) прямой. Из рисунка видно, что это выполняется при х ≤ -2 и х ≥ -2. Поэтому решением неравенства -х2 ≤ -4 являются промежутки (-∞; -2] и [2; +∞). Эти промежутки заштрихованы снизу на оси абсцисс.
в) Проведем прямую y = -1 (горизонтальная прямая). Парабола и прямая пересекаются в точках С и D, абсциссы которых, соответственно, равны ![]() (напомним, что
(напомним, что ![]() — иррациональное число,
— иррациональное число, ![]() ). Следовательно, уравнение -х2 = -2 имеет два корня
). Следовательно, уравнение -х2 = -2 имеет два корня ![]()
г) Графический смысл неравенства -х2 > -2: надо найти такие значения х, при которых точки параболы лежат выше прямой. Из рисунка видно, что это выполняется при ![]() Поэтому решением неравенства -х2 > -2 является промежуток
Поэтому решением неравенства -х2 > -2 является промежуток ![]() Этот промежуток заштрихован сверху на оси абсцисс. Пустые кружки указывают, что граничные точки решением не являются.
Этот промежуток заштрихован сверху на оси абсцисс. Пустые кружки указывают, что граничные точки решением не являются.
Рассмотрим аналогичную более сложную задачу.
Пример 4
Решим графически: а) уравнение -х2 = х - 2, б) неравенство -х2 ≥ х - 2.
Построим графики функций у = -х2 (парабола) и у = х - 2 (прямая).
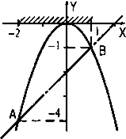
а) Видно, что парабола и прямая пересекаются в двух точках А и В, абсциссы которых, соответственно, равны х = -2 и x = 1. Следовательно, уравнение -х2 = х - 2 имеет два корня х1 = -2 и x2 = 1.
б) Графический смысл неравенства -х2 ≥ х - 2: надо найти такие значения x, при которых точки параболы лежат не ниже (выше или на уровне) прямой. Из рисунка видно, что это выполняется при -2 ≤ х ≤ 1. Поэтому решением неравенства -х2 ≥ х - 2 является промежуток [-2; 1].
Пример 5
Найти значение коэффициента a, при котором одна из точек пересечения параболы у = ах2 и прямой у = 5х - 2 имеет абсциссу x = -2. Найти координаты точек пересечения.
Координаты точки пересечения параболы и прямой являются решением системы уравнений ![]() При этом для одного решения известна величина х = -2. Рассмотрим два способа решения такой системы.
При этом для одного решения известна величина х = -2. Рассмотрим два способа решения такой системы.
1 способ. Подставим известное решение х = -2 во второе уравнение системы и найдем: у = 5 · (-2) - 2 = -12. Таким образом, определили координаты одной точки пересечения прямой и параболы (-2; -12). Теперь подставим значения х = -2 и у = -12 в первое уравнение системы: -12 = а · (-2)2 или -12 = 4a, откуда а = -3. Поэтому данная парабола имеет уравнение у = -3х2.
Теперь найдем координаты второй точки пересечения параболы у = -3х2 и прямой у = 5х - 2. Для этого решим систему уравнении ![]() при этом известно одно решение (-2; -12). Приравняем правые части уравнений системы и получим: -3х2 = 5х - 2 или 0 = 3х2 + 5х - 2. Найдем корни этого квадратного уравнения
при этом известно одно решение (-2; -12). Приравняем правые части уравнений системы и получим: -3х2 = 5х - 2 или 0 = 3х2 + 5х - 2. Найдем корни этого квадратного уравнения ![]() т. е. x1 = 2/6 = 1/3 и x2 = -12/6 = -2 (известное решение). Из любого уравнения, например первого, определим ординату второй точки пересечения параболы и прямой: y = -3 · (1/3)2 = -1/3. Итак, при а = -3 парабола и прямая пересекаются в точках (-2; -12) и (1/3; -1/3).
т. е. x1 = 2/6 = 1/3 и x2 = -12/6 = -2 (известное решение). Из любого уравнения, например первого, определим ординату второй точки пересечения параболы и прямой: y = -3 · (1/3)2 = -1/3. Итак, при а = -3 парабола и прямая пересекаются в точках (-2; -12) и (1/3; -1/3).
2 способ. Приравняем правые части уравнений системы ![]() и получим квадратное уравнение ах2 = 5х - 2. Так как одно решение этого уравнения известно х = -2, то подставим его в уравнение: а · (-2)2 = 5 · (- 2) – 2 или 4а = -12, откуда значение параметра а = -3.
и получим квадратное уравнение ах2 = 5х - 2. Так как одно решение этого уравнения известно х = -2, то подставим его в уравнение: а · (-2)2 = 5 · (- 2) – 2 или 4а = -12, откуда значение параметра а = -3.
Подставим это значение в уравнение ах2 = 5х - 2 или 0 = 3х2 + 5х - 2. Так как один корень х1 = -2 этого уравнения известен, то по теореме Виета получим x1x2 = -2/3 или -2х2 = -2/3, откуда x2 = 1/3. Для абсцисс точек пересечения х1 = -2 и х2 = 1/3 из уравнения параболы у = -3х2 найдем ординаты этих точек: у1 = -3 · (-2)2 = -12 и y2 = -3 · (1/3)2 = -1/3, соответственно. Следовательно, при a = -3 парабола и прямая пересекаются в точках (-2; -12) и (1/3; -1/3).
Пример 6
При каких значениях параметров а и k парабола у = ах2 и прямая у = kх - 4 пересекаются в точках с абсциссами х = 1 и х = -4? Найти ординаты точек пересечения.
Координаты точек пересечения прямой и параболы являются решениями системы уравнений ![]() Приравняем правые части этих уравнений и получим квадратное уравнение ах2 = kх - 4 с параметрами а и k. Решения этого уравнения х1 = 4 и х2 = -4 известны. Подставив эти значения в уравнение, получим систему двух линейных уравнений для нахождения а и k:
Приравняем правые части этих уравнений и получим квадратное уравнение ах2 = kх - 4 с параметрами а и k. Решения этого уравнения х1 = 4 и х2 = -4 известны. Подставив эти значения в уравнение, получим систему двух линейных уравнений для нахождения а и k: ![]() или
или ![]() 1 Сложив уравнения системы, найдем 5а = -5. Откуда а = -1. Тогда, например, из первого уравнения получим -1 – k = -4, откуда k = 3. Следовательно, в задаче рассматривается пересечение параболы y = -x2 и прямой у = 3х - 4.
1 Сложив уравнения системы, найдем 5а = -5. Откуда а = -1. Тогда, например, из первого уравнения получим -1 – k = -4, откуда k = 3. Следовательно, в задаче рассматривается пересечение параболы y = -x2 и прямой у = 3х - 4.
Зная абсциссы точек пересечения, используя уравнение параболы или прямой, легко найти и ординаты. Получим: у1 = -х12 = -12 = -1 и y2 = -х22 = -(-4)2 = -16.
IV. Контрольные вопросы
1. Как получить из графика функции у = х2 график функции: а) у = 3х2, б) y = 1/4х2, в) у = -3х2, г) у = -1/4х2?
2. Укажите ось симметрии и вершину параболы у = ах2.
3. Как направлены ветви параболы у = ах2?
4. Промежутки возрастания и убывания функции у = ах2.
V. Задание на уроке
№ 596 (1, 4); 598 (4); 599 (1, 2); 601 (1); 603; 605 (1,4); 606.
VI. Задание на дом
№ 595; 599 (3, 4); 601 (2); 602; 605 (2, 3); 607.
VII. Творческие задания
1. Графически решите уравнение или неравенство.
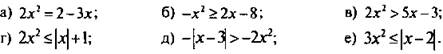
Ответы: ![]()
![]()
2. При каких значениях параметров а и k парабола у = ах2 и прямая у = kх + 3 пересекаются в точках с абсциссами х = -1 и х = 3/2? Найти ординаты точек пересечения.
Ответ: а = 2, k = 1, у1 = 2, у2 = 4,5.
3. При каких значениях параметров а и b парабола у = ах2 и прямая у = x + b пересекаются в точках с абсциссами х = -2 и х = 5/2. Найти ординаты точек пересечения.
Ответ: а = 2, b = -10, y1 = 8, y2 = 12,5.
4. При каких значениях параметров а, b и k прямая у = kх + b проходит через точку (1; 3) и пересекается с параболой у = ах2 в точках с абсциссами х = 1/3 и х = -2? Найти ординаты точек пересечения.
Ответ: а = -3, b = -2, k = 5, у1 = -1/3, у2 = -12.
VIII. Подведение итогов урока