Первое понятие о методе интервалов - МЕТОД ИНТЕРВАЛОВ - КВАДРАТНЫЕ НЕРАВЕНСТВА

Цель: рассмотрение метода интервалов и его использование для решения квадратных неравенств, неравенств, связанных с многочленами, и рациональных неравенств.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Графически решите неравенство:

2. При каких значениях параметра а уравнение 7х2 - 3х + 2а = 0 не имеет решений?

Вариант 2

1. Графически решите неравенство:

2. При каких значениях параметра а уравнение 3х2 - 4х + 5а = 0 не имеет решений?

III. Изучение нового материала (основные понятия)

При решении различных типов неравенств широко используется метод интервалов. Это наиболее универсальный и мощный метод решения всех неравенств (начиная от линейных и кончая тригонометрическими и логарифмическими). Так же метод эффективен и в случае неравенств, содержащих различные функции (например, многочлены и иррациональные функции). Поясним метод интервалов на примерах.

Пример 1

Выясним, при каких значениях х квадратный трехчлен 2х2 + 5х - 3 принимает положительные значения, а при каких — отрицательные.

Найдем корни уравнения 2х2 + 5х - 3 = 0 и получим х1 = -3 и х2 = 1/2. Разложим данный многочлен на множители

Нанесем точки x1 = -3 и х2 = 1/2 на числовую ось. Эти точки разбивают ось натри интервала(промежутка): х ≤ -3 и -3 < х < 1/2 и х ≥ 1/2. Теперь расставим знаки выражения в каждом интервале.

На промежутке х < -3 оба множителя х – 1/2 и х + 3 отрицательны, их произведение положительно. Поэтому выражение 2х2 + 5х - 3 положительно (поставлен знак «+»). В точке х = -3 множитель х + 3 равен 0 и выражение 2х2 + 5х - 3 = 0. В интервале -3 < х < 1/2 множитель х + 3 меняет знак и х + 3 > 0. Поэтому произведение и выражение 2х2 + 5х - 3 отрицательно (поставлен знак «—»). В точке x = 1/2 множитель x – 1/2 равен 0 и выражение 2х2 + 5х - 3 = 0. В промежутке х > 1/2 множитель x – 1/2 меняет знак и х – 1/2 > 0. Поэтому произведение и выражение 2х2 + 5х - 3 положительно (поставлен знак «+»).

Таким образом, выражение 2х2 + 5х - 3 положительно при х < -3 и х > 1/2 и отрицательно при -3 < х < 1/2.

Теперь предварительно сформулируем алгоритм решения задачи об определении знака квадратного трехчлена:

1. Находим корни квадратного трехчлена.

2. Отмечаем эти корни на числовой оси.

3. Определяем знак квадратного трехчлена в любом интервале.

4. Расставляем знаки на остальных интервалах в порядке чередования.

Таким же способом можно решать неравенства, содержащие многочлены более высокого порядка.

Пример 2

Решим неравенство х4 - 13х2 + 36 ≥ 0.

Найдем корни многочлена четвертой степени х4 - 13х2 + 36. Для этого решим биквадратное уравнение х4 - 13х2 + 36 = 0. Введем новую переменную t = x2 и получим квадратное уравнение t2 – 13t + 36 = 0. Корни этого уравнения t1 = 4 и t2 = 9. Вернемся к старой переменной и получим неполные квадратные уравнения: x2 = 4 (корни х1,2 = ±2) и х2 = 9 (корни х1,2 = ±3). Отметим эти корни на числовой оси.

Они разбивают ось на пять интервалов. Определим знак многочлена х4 - 13х2 + З6 в любом промежутке, например в третьем. Подставим любую точку этого промежутка (не совпадающую с его концами), например, х = 1 в выражение х4 - 13х2 + 36 и получим 1 - 13 + 36 = 24 > 0. Таким образом, в точках третьего интервала выражение х4 - 13х2 + 36 положительно. Расставляем знаки на остальных интервалах в порядке чередования. Выписываем те промежутки, на которых стоит знак «+» и получаем решение неравенства х4 - 13х2 + 36 ≥ 0 : х ≤ -3, -2 ≤ х ≤ 2 и х ≥ 3.

Теперь рассмотрим ситуацию, когда многочлен имеет несколько одинаковых корней.

Пример 3

Решим неравенство

Найдем корни данного многочлена. Произведение множителей равно нулю, если один из них равен нулю. Получаем уравнения: (корни х1 = х2 = 1), х = 0 (корень х3 = 0), (корни х4 = х5 = х6 = -3 ), x - 2 = 0 (корень х7 = 2 ). Отметим эти корни на числовой оси.

Они разбивают ось на пять промежутков. Теперь расставим знаки данного выражения в этих интервалах. При этом обратим внимание на особенности изменения знака выражения, связанные с несколькими одинаковыми корнями.

Если корень встречается четное количество раз (говорят еще, что корень имеет четную кратность), то при проходе через такой корень знак выражения не меняется. В данном примере корень второй (четной) кратности х = 1. Очевидно, что выражение (x - 12 ≥ 0 при всех х. Поэтому данное выражение при х = 1 обращается в ноль, но знака при этом не меняет. Тогда в интервалах 3 и 4 выражение имеет одинаковый знак. Так как по сравнению с примерами 1, 2 в точке х = 1 проявляются особенности в изменении знака, то обведем эту точку на числовой оси.

Если корень встречается нечетное количество раз (корень нечетной кратности), то при проходе через такой корень знак выражения меняется на противоположный. В данном примере корень третьей (нечетной) кратности х = -3. Очевидно, что выражение (х + 3)3 слева и справа от точки х = -3 имеет противоположные знаки. Поэтому выражение при проходе через точку х = -3 меняет знак. Очевидно, что корни х = 0 и х = 2 также нечетной (первой) кратности. Следовательно, все вышеизложенное относится и к этим корням.

Определим знак выражения например, при х = 6 (пятый интервал) и получим, что оно положительно. Расставим знаки в остальных промежутках, учитывая, что при переходе от четвертого к третьему интервалу знак выражения не меняется. Теперь можно записать решение данного неравенства: -3 ≤ х ≤ 0, х = 1, х ≥ 2.

Рассмотрим еще один аналогичный пример.

Пример 4

Решим неравенство

Прежде всего найдем корни данного многочлена. Получаем уравнения: (2x – 4)6 = 0 (корень х = 2 четной кратности), (3 + х)2 = 0 (корень х = -3 четной кратности), (6х – 4)3 = 0 (корень x = 2/3), 4 - х = 0 (корень х = 4). Отметим эти корни на числовой оси.

Они разбивают ось на пять интервалов. Определим знак данного выражения, например, при х = 0 и увидим, что он отрицательный. С учетом особенностей изменения знака выражения расставим знаки в других интервалах. Так как данное выражение должно быть неположительным, то на основании приведенной диаграммы знаков выписываем ответ: х ≤ 2/3, х = 2, х ≥ 4.

Рассмотренный метод интервалов используется и при решении рациональных неравенств.

Пример 5

Решим неравенство

Найдем корни квадратных трехчленов, стоящих в числителе и знаменателе дроби. Решая квадратное уравнение 2х2 + 5х - 3 = 0, найдем корни х1 = -3 и х2 = 1/2. Решая уравнение 3х2 + 4х + 1 = 0, получим корни х3 = -1 и х4 = -1/3. Отметим все эти корни х1, х2, х3, х4 на числовой оси. Так как делить на ноль нельзя, то точки х3 и х4 в ответ входить не могут (несмотря на то, что неравенство нестрогое).

Поэтому отметим такие точки пустыми кружками. Возникает пять интервалов. В любой точке определяем знак данной дроби. Например, при х = 0 получаем -3/1 = -3 < 0. Расставляем знаки данного выражения в остальных промежутках, учитывая чередование знаков. На основании диаграммы выписываем ответ: х ≤ -3, -1 < х < -1/3, x ≥ 1/2.

Пример 6

Решим неравенство

Приведем неравенство к виду, аналогичному предыдущему примеру. Для этого перенесем дробь из правой части в левую и получим Приведем дроби к общему знаменателю: Раскроем скобки в числителе и приведем подобные члены Числитель дроби в ноль не обращается. Корни знаменателя х1 = -1, х2 = 3 и х3 = 7. Отметим эти корни на числовой оси. Возникает четыре интервала.

Определим, например, при х = 0 знак выражения и получим, что он положительный. Расставляем знаки этой дроби в остальных интервалах. На основании диаграммы выписывает ответ: х < -1, 3 < х < 7.

Также удобно использовать метод интервалов при решении неравенств, содержащих модули и параметры.

Пример 7

Решим неравенство

Найдем корни числителя и знаменателя. Решим уравнение: |х - 1| - 2 = 0, или |х - 1| = 2, или х – 1 = ±2 , откуда х = 1 ± 2, т. е. х1 = -1 и х2 = 3. Решим уравнение: |x - 2| - 1 = 0, или |х - 2| = 1, или х - 2 = ±1, откуда х = 2 ± 1, т. е. х3 = 1 и х4 = 3. Отметим эти корни на числовой оси. При этом учтем, что х = 3 корень четной кратности и х ≠ 1 и х ≠ 3.

Определим знак данной дроби, например, при x = 10 и получим, что он положительный. Расставим знаки дроби в промежутках. На основании диаграммы знаков выписываем ответ: х ≤ -1, 1 < х < 3, х > 3.

Пример 8

Решим неравенство х2 - 2ах - 4х + 8а ≥ 0.

Найдем корни квадратного трехчлена. Для этого решим квадратное уравнение х2 - 2х(а + 2) + 8а = 0 и получим т. е. х1 = 2а и х2 = 4. Теперь надо нанести эти корни на числовую ось. При этом точка х = 2а может оказаться левее, совпасть или находиться правее точки х = 4. Поэтому такие три случая необходимо рассмотреть. При этом при больших значениях х данный квадратный трехчлен принимает положительные значения.

а) Пусть 2а < 4, т. е. a < 2. Тогда диаграмма знаков имеет вид, представленный на рисунке. Решение неравенства при a < 2: x ≤ 2a, х ≥ 4.

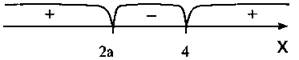
б) Пусть 2а = 4, т. е. а = 2. Тогда диаграмма знаков изображена на рисунке. Решение неравенства при а = 2 — любое значение х.

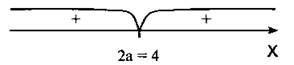
в) Пусть 2a > 4 , т. е. а > 2. Тогда диаграмма знаков изображена рисунке. Решение неравенства при а > 2: х ≤ 4, х ≥ 2а.

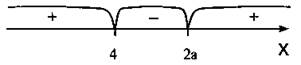
Теперь выпишем полный ответ задачи: при а < 2 х ≤ 2а, х ≥ 4; при а = 2 х — любое число; при а > 2 х ≤ 4, х ≥ 2а.

Как ранее было отмечено, метод интервалов успешно используется при решении неравенств, содержащих разнотипные функции.

Пример 9

Решим неравенство

Найдем корни числителя и знаменателя. Решим уравнение: или или х - 1 = 4, откуда х1 = 5. Решая уравнение х2 - 8х + 15 = 0, найдем корни х2 = 3 и х3 = 5. Отметим эти корни на числовой оси. При этом учтем, что подкоренное выражение неотрицательно, т. е. х - 1 ≥ 0, откуда х ≥ 1.

Также учтем, что х = 5 — корень второй кратности. Найдем значение данной дроби, например, при х = 17 и увидим, что это значение положительно. Расставим знаки выражения в остальных интервалах. На основании диаграммы знаков выпишем решение данного неравенства: 1 ≤ х < 3.

Уточним теперь алгоритм использования метода интервалов для решения рациональных неравенств (в частности, для решения целых неравенств):

1. Найти корни числителя и знаменателя и определить их кратность.

2. Нанести эти корни на числовую ось.

3. В любой точке (не совпадающей с корнями) определить знак данного выражения.

4. Построить диаграмму знаков выражения с учетом кратности корней. Учесть, что при проходе через корень нечетной кратности знак выражения меняется, при проходе через корень четной кратности знак сохраняется.

5. Выписать решение неравенства, учитывая, что корни знаменателя в ответ не входят.

IV. Контрольные вопросы

1. Объясните, как методом интервалов можно решить квадратное неравенство (можно на примере).

2. Как можно решить методом интервалов рациональное неравенство (можно на примере)?

3. Какие корни называются кратными?

4. Как ведет себя знак выражения при проходе через корень четной и нечетной кратности?

V. Задание на уроке

№ 674 (1); 675 (1, 4); 676 (3, 5); 677 (3); 678 (1, 3, 5); 679 (1, 5); 680 (1, 3); 681 (5); 682 (1).

VI. Задание на дом

N° 674 (2); 675 (2, 3); 676 (4, 6); 677 (4); 678 (1, 3, 5); 679 (2, 6); 680 (2, 4); 681 (6); 682 (2).

VII. Творческие задания

Методом интервалов решите неравенство:

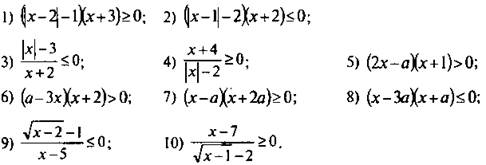
Ответы: 1) -3 ≤ х ≤ 1, х ≥ 3.

2) х ≤ -2, -1 ≤ х ≤ 3.

3) x ≤ -3, -2 < х ≤ 3.

4) -4 ≤ х < -2; х > 2.

5) при а < -2 x < a/2, x > -1; при а = -2х < -1, х > -1; при a > -2х < -1 x > a/2;

6) при а < 6a/3 < х < -2; при а = -6 решений нет; при а > -6 – 2 < х < a/3;

7) при а < 0 х ≤ a, х ≥ -2a; при а = 0 х — любое число; при а > 0 х ≤ -2а х ≥ а;

8) при а < 0 3а ≤ х ≤ -а; при а = 0 х = 0; при а > 0 - а ≤ х ≤ 3а;

9) 3 ≤ х < 5.

10) 1 ≤ x < 5, x ≥ 7.