Поурочные разработки по Алгебре 8 класс
Урок 1 - ОСНОВНЫЕ ПОНЯТИЯ
Цели: провести анализ тестирования; ввести понятие алгебраической дроби и допустимых значений для дроби; формировать умение определять область допустимых значений для любой дроби.
Ход урока
I. Организационный момент.
II. Анализ тестирования.
Выставить оценки за тестирование. Задания, с которыми учащиеся плохо справились, разобрать на доске. Желательно разобрать 5 и 6 задания обоих вариантов.
В а р и а н т 1
Задание 5.
Чему равно ab, если a – b = 1 и (a2 – b2)(a – b) = 9?
Р е ш е н и е:
![]()
Теперь составим систему уравнений и решим ее

![]()
О т в е т: 20.
Задание 6.
Разложите на множители b2 + ab – 2a2 – b + a.
Р е ш е н и е:
![]()
![]()
![]()
![]()
О т в е т: ![]()
В а р и а н т 2
Задание 5.
Вычислите a3 + 3a2 – 9a – 27, если a2 + 6a + 9 = 0.
Р е ш е н и е:
![]()
![]()
![]()
О т в е т: 0.
Задание 6.
Разложите на множители a3 + 9a2 + 27a + 19.
Р е ш е н и е:
![]()
![]()
![]()
![]()
О т в е т: ![]()
III. Объяснение нового материала.
Вспомнить понятие дроби и выписать несколько дробей на доске. Затем ввести понятие алгебраической дроби.
1) Определить, является ли данная дробь алгебраической:
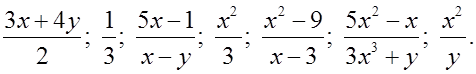
2) Рассмотреть дробь  и найти ее значения при заданных переменных:
и найти ее значения при заданных переменных:
а) x = 1, y = 1; б) x = 2, y = 3; в) x = 3, y = –1.
Сделать соответствующие выводы: нельзя найти значение данной дроби при переменной х = 2 и при переменной у = –1, так как знаменатель дроби обращается в нуль, а на нуль делить нельзя.
Ввести понятие области допустимых значений.
Допустимые значения дроби – это такие значения, при которых знаменатель дроби не обращается в нуль.
IV. Закрепление нового материала.
1) Решить задания 1.2; 1.3 (а); 1.4 (г); 1.5; 1.8.
2) Сравнить значения алгебраических дробей 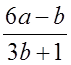 и
и  при заданных значениях переменных:
при заданных значениях переменных:
а) a = 8, b = 3; б) a = 1, b = 3; в) a = 50, b = 8.
V. Подведение итогов.
Домашнее задание: прочитать и изучить теорию из учебника на с. 7–10. Решить задачи 1.1; 1.3 (б, г); 1.4 (а, в); 1.10.