Поурочные разработки по Алгебре 8 класс
РАЦИОНАЛЬНЫЕ ЧИСЛА
Цели: провести анализ контрольной работы; ввести понятие множества натуральных, действительных, рациональных чисел; формировать умение различать множества чисел.
Ход урока
I. Организационный момент.
II. Анализ контрольной работы.
Рассмотреть задания, с которыми не справилось большинство учащихся.
В а р и а н т 1
Задание 4.
Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шел 18 км по озеру. Какова собственная скорость катера, если скорость течения реки 3 км/ч?
Р е ш е н и е:
Пусть собственная скорость катера x км/ч, тогда составим таблицу:
V (км/ч) |
t (ч) |
S (км) |
|
по течению |
x + 3 |
|
5 |
против течения |
x – 3 |
|
12 |
по озеру |
x |
|
18 |
Так как время, затраченное катером по течению и против течения равно времени, которое катер бы затратил на расстояние 18 км по озеру, то составим уравнение:

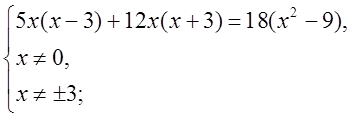
5x2 – 15x + 12x2 + 36x = 18x2 – 162;
–x2 + 21x + 162 = 0;
x2 – 21x – 162 = 0;
D = 441 + 648 = 1089 = 332;
D > 0, имеем два действительных корня.
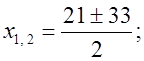
X1 = 27, x2 = –6.
–6 не подходит по условию задачи (время всегда положительно), значит собственная скорость движения катера 27 км/ч.
О т в е т: 27 км/ч.
Задание 5*.
Не решая уравнения 2x2 – 3x + 6 = 0, найти значение выражения ![]()
Р е ш е н и е:
![]()

Для использования теоремы Виета необходимо, чтобы первый коэффициент квадратного уравнения был равен единице:
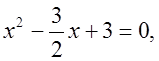 значит
значит 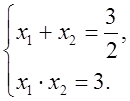

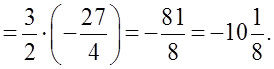
О т в е т: 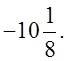
III. Объяснение нового материала.
Учитель систематизирует знания учащихся о рациональных числах, вводит обозначение множества чисел.
1) Натуральные числа – это множество чисел, употребляемых при счете.
Обозначается это множество буквой N. Для сокращения записи математических утверждений используют математические символы. 2 N (число два принадлежит множеству натуральных чисел).
Целые числа – это множество натуральных чисел, им противоположных и ноль. Обозначаются буквой Z.
Рациональные числа (Q) – это множество чисел вида ![]() (где n – натуральные числа, m – целые числа).
(где n – натуральные числа, m – целые числа).
Для более четкого понятия математической ситуации N Z Q проводится игра «хлопушки».
Учитель зачитывает утверждения – ученики хлопают в том случае, если утверждение верно:
· 5 является целым числом;
· 11,5 является натуральным числом;
· –1,5 является целым числом;
· 2,7 является рациональным числом;
· –2 является целым и рациональным числом;
· ![]() – является рациональным и натуральным числом;
– является рациональным и натуральным числом;
· 100 – является натуральным, целым и рациональным числом.
Затем вводится понятие бесконечной периодической дроби, периода. На конкретных примерах показывается, что любая бесконечная десятичная периодическая дробь есть рациональное число и любое рациональное число представимо в виде бесконечной десятичной периодической дроби.
IV. Закрепление нового материала.
1) Устно разобрать задания № 9.3; 9.4; 9.7; 9.9.
2) Письменно рассмотреть задачи № 9.10; 9.12; 9.13; 9.14; 9.16; 9.20 (а, г); 9.22 (а, г); 9.24.
3) В классе с высоким уровнем подготовки можно решить примеры, включающие в себя периодические дроби:
а) 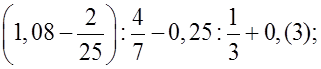
б) 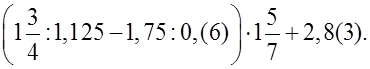
4) Решить уравнение 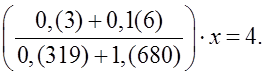
V. Подведение итогов.
Домашнее задание: изучить материалы параграфа 9. Решить задачи № 9.8; 9.15; 9.20 (б, в); 9.22 (б, в).