Поурочные разработки по Алгебре 8 класс
Урок 2 - ТЕОРЕМА ВИЕТА
Цели: повторить терему Виета; объяснить правила разложения многочленов на множители; развивать умение решать квадратные уравнения различными способами, формировать умение раскладывать многочлены на множители, сокращать дроби.
Ход урока
I. Организационный момент.
II. Индивидуальная работа.
К доске вызываются четыре ученика для выполнения различных заданий с помощью теоремы Виета.
Карточка 1
Решить уравнение и проверить его корни по теореме Виета:
x2 + x – 20 = 0.
Карточка 2
Составить уравнение, для которого корнями будут являться числа 1 и –3.
Карточка 3
При каком значении переменной b один из корней уравнения x2 – bx + 15 = 0 равен 3.
Карточка 4
Не решая уравнения 3x2 + x – 30 = 0 найти значение выражения 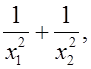 где x1 и x2 являются корнями данного уравнения.
где x1 и x2 являются корнями данного уравнения.
III. Актуализация знаний.
Во время проведения индивидуальной работы остальные учащиеся класса решают задание № 29.8.
После некоторого времени проверяются задания на доске, в тетрадях, уравнения из домашнего задания. После чего устно разбираются уравнения № 29.1; 29.4, письменно решается задание № 29.11.
IV. Объяснение нового материала.
Учитель доказывает теорему о разложении многочлена на множители согласно параграфу, и показывает ее применение на примерах:
1) Разложить на множители:
а) x2 + 6x – 7;
б) 3x2 + 2x – 5.
2) Сократить дробь 
V. Закрепление нового материала.
1) Из учебника разобрать решение заданий № 29.16; 29.17; 29.20.
Сильным ученикам предлагается решить задания 1) № 29.29; 29.31; 29.37.
2) Не решая уравнения ax2 + bx + c = 0, найдите:
а) ![]() б)
б) 
Вычислите значение данных выражений для уравнения 3x2 – 2x – 3 = 0.
3) Не решая уравнения 2x2 – 3x – 11 = 0, найдите 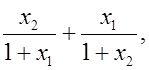 где x1, x2 его корни.
где x1, x2 его корни.
Р е ш е н и е:
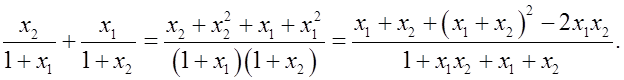
Для использования теоремы Виета нужно сделать уравнение приведенным:
 тогда по теореме Виета
тогда по теореме Виета 

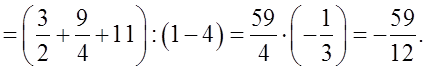
Ответ: 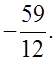
VI. Подведение итогов.
Домашнее задание: решить задачи № 29.15; 29.19; 29.39; 29.48.