Урок 2 - РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ

Цели: рассмотреть решение квадратных неравенств различного уровня сложности; развивать умение решать неравенства разными способами.

Ход урока

I. Организационный момент.

II. Индивидуальная работа.

К доске вызываются четыре ученика для самостоятельного решения неравенств с карточек:

Карточка 1 x2 – 2x – 35 > 0	Карточка 2 x2 – 5x + 9 < 0
Карточка 3 –x2 + 6x – 5 ≥ 0	Карточка 4 x2 – 10x + 25 ≤ 0

III. Актуализация знаний.

Во время индивидуальной работы остальные учащиеся класса самостоятельно выполняют № 34.9.

IV. Решение задач.

1) На конкретном примере учащимся предлагается еще один способ решения квадратных неравенств – метод интервалов:

–2x2 + 3x + 9 < 0

2x2 – 3x – 9 > 0

Разложим квадратный трехчлен 2x2 – 3x – 9 на множители. Корнями трехчлена являются числа x1 = –1,5; x2 = 3.

2x2 – 3x – 9 = 2(x + 1,5)(x – 3).

Отметим на числовой прямой корни трехчлена

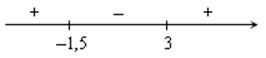
Определим знаки произведения 2(x + 1,5)(x – 3) на каждом из этих промежутков.

при x < –1,5 x + 1,5< 0, x – 3 < 0, а (x + 1,5)(x – 3) > 0;

при –1,5 < x < 3 (x + 1,5)(x – 3) < 0;

при x > 3 (x + 1,5)(x – 3) > 0.

Квадратный трехчлен принимает положительное значение для любого x (–∞; –1,5)(3, +∞).

2) Рассмотреть решение неполных квадратных неравенств № 34.16; 34.18.

3) Решить неравенства № 34.20; 34.21 (б); 34.22 (б); 34.31; 34.32.

V. Обучающая самостоятельная работа.

Вариант 1	Вариант 2
Решите неравенства:
а) 9x2 ≤ –25 – 30x; б) –x2 > 16; в) 3x2 – x < 0; г) –x2 – 4 ≤ 4x; д) x2 – 2x > –1; е) 6x2 ≥ 15 – x.	а) x2 ≥ –12x – 36; б) 7x2 + 12x < –5; в) 4x – x2 < 7; г) 6x2 – 4 ≥ 0; д) –10x2 > 17x; е) 9x2 – 24x ≤ –16.

Ответы данной самостоятельной работы проверяется на уроке. Неравенства, которые вызвали затруднения, разбираются на доске. Оценки выставляются выборочно.

VI. Подведение итогов.

Домашнее задание: решить задачи № 34.15; 34.19; 34.21(а); 34.30.