Зачетная работа по теме «Квадратичная функция» - Степенная функция. Корень n-й степени - Квадратичная функция

Цель: проверка знаний учащихся по вариантам одинаковой сложности.

Ход урока

I. Сообщение темы и цели урока

II. Варианты зачетной работ.

Вариант 1

А

1. Найдите область определения функции

2. Найдите область значений функции у = 2х2 - 8х.

3. Сократите дробь

4. Упростите выражение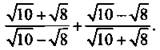

5. Пусть x1 и x2 — корни трехчлена 2х2 - 5х + 1. Найдите значение выражения x1х22 + x12х2.

6. Постройте график функции.

В

7. Упростите выражение

8. Найдите наименьшее значение функции При каких значениях х оно достигается?

9. Найдите координаты точек прямой у = 6х - 35, равноудаленных от осей координат.

10. Постройте график функции

С

11. Найдите промежутки возрастания и убывания функции

12. Упростите выражение при a ≤ 4.

13. Прямая проходит через точку (0; -1) и касается гиперболы у = 1/x. В какой точке эта прямая пересекает ось абсцисс.

Вариант .

А

1. Найдите область определения функции

2. Найдите область значений функции у = 4х - 2х2.

3. Сократите дробь

4. Упростите выражение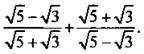

5. Пусть х1 и х2 - корни трехчлена 3х2 - 2х - 4. Найдите значение выражения x12х2 + x1х22.

6. Постройте график функции.

В

7. Упростите выражение

8. Найдите наименьшее значение функции При каких значениях х оно достигается?

9. Найдите координаты точек прямой у = -5х - 24, равноудаленных от осей координат.

10. Постройте график функции

С

11. Найдите промежутки возрастания и убывания функции

12. Упростите выражение при а ≥ 3.

13. Прямая проходит через точку (0; 3) и касается гиперболы у = 3/x. В какой точке эта прямая пересекает ось абсцисс.

III. Ответы и решени.

Вариант 1

1. Ответ: D(у) = (-1; 2].

2. Ответ: Е(у) = [-8; +∞).

3. Ответ:

4. Ответ: 18.

5. Ответ: 5/4.

6. Ответ: график построен.

7. Ответ: 18/5.

8. ymin = 6 при x = -0,5 и x = 1,5.

9. Ответ: (5; -5) и (7; 7).

10. Ответ: график построен.

11. Раскроем знаки модуля и найдем вид функции у = 3х + 2|x - 2| - |x + 1| - 2 в каждом промежутке:

а) при х ≤ -1 получаем: - функция возрастает;

б) при -1 ≤ х ≤ 2 имеем: - функция постоянна;

в) при х ≥ 2 получаем: — функция возрастает.

Ответ: промежутки возрастания (-∞; -1] и [2; +∞), промежутков убывания нет.

12. Упростим выражение Учтено, что

Ответ: 7 - а.

13. Так как прямая проходит через точку (0; -1), то ее вид: у = ах - 1. Если прямая у = ах - 1 и гипербола у = 1/x касаются, то уравнение ах - 1 = 1/x, или ах2 - х - 1 = 0, имеет единственный корень. Поэтому дискриминант D = 1 + 4а = 0, откуда а = -1/4. Прямая у = -1/4х - 1 пересекает ось абсцисс в точке x = -4.

Ответ: х = -4.

Вариант 2

1. Ответ: D(y) = [1; 4).

2. Ответ: Е(у) = (-∞; 2].

3. Ответ:

4. Ответ: 8.

5. Ответ: -10/9.

6. Ответ: график построен.

7. Ответ: 35/12.

8. ymax = 7 при х = -2 и х = 2/3.

9. Ответ: (-4; -4) и (-6; 6).

10. Ответ: график построен.

11. Раскроем знаки модуля и найдем вид функции у = 2х + 3|x - 1| - 4|x + 2| - 1 в каждом промежутке:

а) при х ≤ -2 получаем: у = 2х - 3(х - 1) + 4(x + 2) - 1 = 3х + 10 - функция возрастает;

б) при -2 ≤ х ≤ 1 имеем: у = 2х - 3(х - 1) - 4(х + 2) - 1 = -5х - 6 - функция убывает;

в) при х ≥ 1 получаем: у = 2х + 3(х - 1) - 4(х + 2) - 1 = х - 12 - функция возрастает.

Ответ: промежутки возрастания (-∞; -2] и [1; +∞), промежуток убывания [-2; 1].

12. Упростим выражение Учтено, что а ≥ 3 и

Ответ: а - 1.

13. Так как прямая проходит через точку (0; 3), то ее вид: у = ах + 3. Если прямая у = ах + 3 и гипербола у = 3/x касаются, то уравнение ах + 3 = 3/x, или ах2 + 3х - 3 = 0, имеет единственный корень. Поэтому дискриминант D = 9 + 12а = 0, откуда а = -3/4. Прямая у = -3/4х + 3 пересекает ось абсцисс в точке х = 4.

Ответ: х = 4.