Итоги контрольной работы - урок 2 - Неравенства с одной переменной - Уравнения и неравенства с одной переменной

Цель: сообщить результаты работы, рассмотреть наиболее типичные ошибки, разобрать трудные задачи.

Ход урока

I. Сообщение темы и цели урока

II. Итоги контрольной работы

III. Ответы и решени.

Ответы

Вариант 1

1. Ответ: а) -1; ±3; б) 3; 7; в) 19/4.

2. Ответ: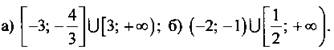

3. Ответ: (-10/3; 10/3).

Вариант 2

1. Ответ: а) 1; ±1/2; б) -2; -1; в) -43/9.

2. Ответ:

3. Ответ: .

Вариант 3

1. Ответ: а) 2; 29/15; -14; б) -1; в) -2; 4.

2. Ответ:

3. Ответ: при a = 0 х = -6 и х = 0; при а = 9 х = -3 и х = 0.

Вариант 4

1. Ответ: а) 1; 4; 16/7; б) -1; в) -3; 5.

2. Ответ:

3. Ответ: при а = 0 х = -1 и х = 0; при а = 1 х = -1/2 и х = 0.

Решения

Вариант 5

1(a). Подберем корень х = 1 уравнения х4 - х3 - 7х2 + х + 6 = 0. Разделив многочлен на х - 1, получим кубическое уравнение х3 - 7х - 6 = 0. Еще раз угадаем корень х = -1. Разделим этот многочлен на х + 1 и получим квадратное уравнение х2 - х - 6 = 0, корни которого х = -2 и х = 3. Таким образом, данное уравнение имеет четыре корня: 1; -1; -2; 3.

Ответ: 1; -1; -2; 3.

1(б). В уравнении выполним вычитание в скобках и получим: 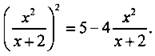Введем новую переменную Получим квадратное уравнение у = 5 - 4у, или у2 + 4у - 5 = 0, корни которого у = 1 и у = -5. Вернемся к старой переменой х.

а) Уравнение или х2 - х - 2 = 0, имеет корни х1 = -1 и х2 = 2.

б) Уравнение или x2 + 5х + 10 = 0, корней не имеет.

Ответ: -1; 2.

1(в). В уравнении уединим первый радикал Возведем обе части уравнения в квадрат: или Вновь возведем в квадрат обе части уравнения: 100 - 20х + х2 = 16х - 28, или х2 - 36х + 128 = 0. Корни этого квадратного уравнения х = 32 и х = 4. Проверка показывает, что корень х = 32 посторонний. Итак, данное уравнение имеет единственное решение х = 4.

Ответ: 4.

2(a). Для решения неравенства запишем его в виде или Введем новую переменную у = |х + 1| и получим квадратное неравенство у2 ≤ 3у, или у2 - 3у ≤ 0, решение которого 0 ≤ у ≤ 3. Вернемся к старой переменной. Имеем неравенство 0 ≤ |х + 1| ≤ 3. Очевидно, что неравенство 0 ≤ |х + 1| выполнено при всех х. Неравенство |х + 1| ≤ 3 равносильно неравенству -3 ≤ х + 1 ≤ 3. Вычтем из всех частей 1 и найдем решение неравенства -4 ≤ х ≤ 2, или х ∈ [-4; 2].

Ответ: х ∈ [-4; 2].

2(б). Проще всего решить неравенство 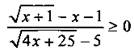методом интервалов. Найдем корни числителя: или или х + 1 = (х + 1)2, или 0 = (х + 1)х, откуда х = -1 и х = 0.

Также найдем корень знаменателя: или или 4х + 25 = 25, откуда х = 0.

Отметим корни числителя и знаменателя на координатной оси (при этом х = 0 - корень второй кратности) и учтем ОДЗ неравенства х ≥ -1.

Определим знак дроби, например, при х = 100: 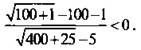Строим диаграмму знаков дроби. Выписываем ответ: х = -1.

Ответ: -1.

3. Рассмотрим уравнение (х2 + 2х + 2)(х2 - 4х + 5) = 1. В множителях выделим полные квадраты: х2 + 2х + 2 = (х + 1)2 + 1 ≥ 1 (равенство достигается при х = -1) и х2 - 4х + 5 = (х - 2)2 + 1 ≥ 1 (равенство достигается при х = 2). Тогда произведение (х2 + 2х + 2)(х2 - 4х + 5) > 1, учитывая, что равенства достигались при разных значениях х. Поэтому данное равенство не выполняется и уравнение не имеет корней.

Ответ: доказано.

Вариант 6

1(a). Подберем корень х = -1 уравнения х4 + х3 - 3х2 - 5х - 2 = 0. Разделив многочлен на х + 1, получим кубическое уравнение х3 - 3х - 2 = 0. Еще раз угадаем корень х = 2. Разделим этот многочлен на х - 2 и получим квадратное уравнение х2 + 2х + 1 = 0, или (х + 1)2 = 0, корни которого х = -1 и х = -1. Таким образом, данное уравнение имеет четыре корня: -1; -1; -1; 2.

Ответ: -1; -1; -1; 2.

1(б). В уравнении выполним сложение в скобках и получим: 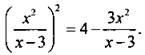Введем новую переменную у = . Получаем квадратное уравнение у2 = 4 - 3у, или у2 + 3у - 4 = 0, корни которого у = -4 и у = 1. Вернемся к старой переменой х.

а) Уравнение или х2 + 4х - 12 = 0, имеет корни х1 = -6 и x2 = 2.

б) Уравнение или х2 - х + 3 = 0, корней не имеет.

Ответ: -6; 2.

1(в). В уравнении уединим первый радикал Возведем обе части уравнения в квадрат: или Вновь возведем в квадрат обе части уравнения: 12х + 4 = 169 - 26х + х2, или 0 = х2 - 38х + 165. Корни этого квадратного уравнения х = 33 и х = 5. Проверка показывает, что корень х = 33 посторонний. Итак, данное уравнение имеет единственное решение х = 5.

Ответ: 5.

2(a). Для решения неравенства запишем его в виде: или Введем новую переменную у = |х - 5| и получим квадратное неравенство у2 ≤ 5у, или у2 - 5у ≤ 0, решение которого 0 ≤ у ≤ 5. Вернемся к старой переменной. Имеем неравенство 0 ≤ |х - 5| ≤ 5. Очевидно, что неравенство 0 ≤ |х - 5| выполнено при всех х. Неравенство |х - 5| ≤ 5 равносильно неравенству -5 ≤ х - 5 ≤ 5. Прибавим ко всем частям 5 и найдем решение неравенства 0 ≤ х ≤ 10, или х ∈ [0; 10].

Ответ: х ∈ [0; 10].

2(б). Проще всего решить неравенство 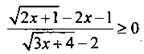методом интервалов. Найдем корни числителя: или или 2х + 1 = (2х + 1)2, или 0 = 2х(2х + 1)х, откуда х = 0 и х = -1/2.

Также найдем корень знаменателя: или или 3х + 4 = 4, откуда х = 0.

Отметим корни числителя и знаменателя на координатной оси (при этом х = 0 - корень второй кратности) и учтем ОДЗ неравенства х ≥ -1/2.

Определим знак дроби, например, при х = 100: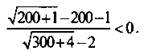

Строим диаграмму знаков дроби. Выписываем ответ: х = -1/2.

Ответ: -1/2.

3. Рассмотрим уравнение (х2 - 2х + 3)(х2 – 6x + 10) = 2. В множителях выделим полные квадраты: х2 - 2х + 3 = (х - 1)2 + 2 ≥ 2 (равенство достигается при х = 1) и х2 - 6х + 10 = (х - 3)2 + 1 ≥ 1 (равенство достигается при х = 3). Тогда произведение (х2 - 2х + 3)(х2 - 6х + 10) > 2, учитывая, что равенства достигались при разных значениях х. Поэтому данное равенство не выполняется и уравнение не имеет корней.

Ответ: доказано.