Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Уравнение с двумя переменными и его график - Уравнения с двумя переменными и их системы - Уравнения и неравенства с двумя переменными
Целы ввести основные понятия и термины темы.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала
Равенство, содержащее две переменные, называют уравнением с двумя переменными (или неизвестными). Решением уравнения с двумя переменными называют пару значений неизвестных, которые обращают это уравнение в верное равенство. Уравнение с двумя переменными может иметь: бесконечное множество решений или ограниченное число решений, а также не иметь решений.
Пример 1
Рассмотрим следующие уравнения с двумя переменными:
а) Уравнение 3х + 7у = 10 (уравнение прямой) имеет бесконечное множество решений.
б) Уравнение |х - 1| + у2 = 0 имеет единственное решение: х = 1, y = 0.
в) Уравнение (х2 - 1)2 + (у2 - 4)2 = 0 имеет четыре решения: х = 1, у = 2; х = 1, у = -2; х = -1, у = 2; х = -1, у = -2.
г) Уравнение |х - 1| + (у - 2)2 = -5 не имеет решений.
Два уравнения, имеющие одно и то же множество решений, называют равносильными.
Пример 2
а) Уравнения |х| + (у - 1)2 = 0 и х2 + |у - 1| = 0 равносильны, т. к. имеют одно и то же решение: х = 0 и у = 1.
б) Уравнение |х| + (у - 1)2 = 0 и x2 + |y2 - 1| = 0 неравносильны, т. к. первое имеет одно решение: х = 0, у = 1, а второе - два решения: х = 0, у = 1 и х = 0, у = -1.
Степень целого уравнения с двумя переменными определяется так же, как и степень целого уравнения с одной переменной. Если одна часть уравнения представляет собой многочлен стандартного вида, а другая - число 0, то степень уравнения считают равной степени этого многочлена. Для определения степени уравнения его заменяют равносильным, одна часть которого - многочлен стандартного вида, а другая - нуль.
Пример 3
Уравнение (х3 + 2у2)2 = х6 - 2х2у равносильно уравнению х6 + 4х3у2 + 4у4 = х6 - 2х2у и равносильно уравнению 2х3у2 + 2у4 + х2у = 0. Поэтому данное уравнение является уравнением пятой степени.
Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Пример 4
а) Графиком уравнения ах + by = с (где а ≠ 0 или b ≠ 0) является прямая.
б) Графиком уравнения у = ах2 + bх + с (где а ≠ 0) является парабола.
в) Графиком уравнения ![]() (где с ≠ 0 и ad - bc ≠ 0) является гипербола.
(где с ≠ 0 и ad - bc ≠ 0) является гипербола.
Рассмотрим еще одно важнейшее и часто встречающееся уравнение - уравнение окружности с центром в точке (а; b) и радиусом R: (х - а)2 + (у - b)2 =R2.
Пример 5
Выведем уравнение окружности.
Рассмотрим окружность с центром в точке 0(а; b) и радиусом R. Выберем произвольную точку А(х; у) на окружности. Проведем отрезки ОВ и АВ параллельно оси абсцисс и оси ординат соответственно.
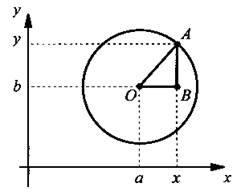
Рассмотрим прямоугольный треугольник ОАВ, в котором катеты OB = |х - а| и АВ = |у - b| и гипотенуза ОА = R. Запишем для этого треугольника теорему Пифагора:
ОВ2 = АВ2 = ОА2, или |х - а|2 + |у - b|2 = R2, или (х - а)2 + (y - b)2 = R2.
Это и есть уравнение окружности. В частности, уравнение окружности с центром в начале координат имеет вид: х2 + у2 = R2.
Пример 6
Построим график уравнения х2 - 2х + у2 + 4у = 0.
Так как в уравнение переменные х и у входят во второй степени (и ниже), то это уравнение окружности. Выделим в уравнении полные квадраты по переменным хну. Для этого запишем уравнение в виде (х2 - 2х + 1) + (у2 + 4y + 4) = 5 или ![]()
Видно, что это уравнение окружности с центром в точке O(1; -2) и радиусом ![]() Теперь легко построить и сам график.
Теперь легко построить и сам график.

Пример 7
Построим график уравнения ![]()
Прежде всего отметим, что у ≥ 0. Возведем обе части уравнения в квадрат: у2 = 4х - х2, или у2 - х2 - 4х = 0. Выделим квадрат разности по переменной х: у2 + (х2 - 4х + 4) = 4, или (х - 2)2 + у2 = 22. Получили уравнение окружности с центром в точке O(2; 0) и радиусом R = 2.
Учитывая ограничение у ≥ 0, имеем верхнюю полуокружность. Теперь можно строить график.
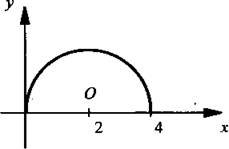
Заметим, что графики уравнений с двумя переменными могут иметь самый разнообразный и даже необычный вид.
III. Контрольные вопросы
1. Определение уравнения с двумя переменными.
2. Что называют решением уравнения с двумя переменными?
3. Какие уравнения называют равносильными?
4. Как определить степень целого уравнения с двумя переменными?
5. Уравнение окружности с центром в точке O(а; b) и радиусом R.
IV. Задание на уроке
№ 395 (а, г); 396 (а, в); 397 (г); 399 (а, д, ж); 402 (а, г); 404 (б); 405 (а); 408; 410; 411 (а).
V. Задание на дом
№ 395 (б, в); 396 (б, г); 397 (в); 399 (б, е, з); 402 (б, в); 404 (а); 405 (в); 406; 409; 411 (б).
VI. Творческие задания
Постройте график уравнения.
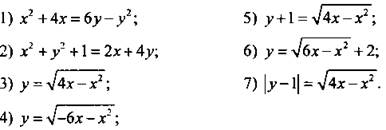
VII. Подведение итогов урока