Формула суммы первых n членов геометрической прогрессии - Геометрическая прогрессия - Арифметическая и геометрическая прогрессии

Цель: получить формулу для суммы членов геометрической прогрессии.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Рекуррентная формула члена геометрической прогрессии.

2. Для геометрической прогрессии 2; 2/3; 2/9; ... найдите: а) пятый член; б) n-й член.

3. В геометрической прогрессии b3 = 7/2 и b6 = 7/16. Найдите b1 и q.

Вариант 2

1. Формула n-го члена геометрической прогрессии.

2. Для геометрической прогрессии 3; 3/2; 3/4; ... найдите: а) пятый член; б) n-й член.

3. В геометрической прогрессии b2 = 5/3 и b5 = 5/81. Найдите b1 и q.

III. Изучение нового материала

Сумма n первых членов вычисляется по формуле или

Пример 1

Получим формулу для вычисления суммы n первых членов геометрической прогрессии.

Рассмотрим сумму и первых членов прогрессии:

Умножим эту величину на q и получим:

Учитывая определение геометрической прогрессии запишем это же равенство:

Вычтем из соотношения [2] выражение [1], тогда в правой части сокращаются члены b2, b3, ..., bn и получаем: откуда (разумеется, для q ≠ 1).

Учитывая, что из этого уравнения находим:

Итак,

Если знаменатель q = 1, то геометрическая прогрессия состоит из одинаковых членов b1. Тогда сумма первых n членов такой прогрессии равна Sn = nb1.

Пример 2

Найдем сумму первых восьми членов геометрической прогрессии, второй член которой равен 6, а четвертый равен 24.

Сначала определим характеристики геометрической прогрессии. Используя формулу n-го члена, запишем условия задачи: 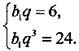Разделив второе уравнение на первое, получим: q2 = = 4, откуда q = ±2.

Для q = 2 найдем: b1 = 6/q = 3 и сумму

Для q = -2 получим: b1 = -3 и сумму

Пример 3

Сумма первого и пятого членов геометрической прогрессии равна 51, а сумма второго и шестого членов равна 102. Сколько членов этой профессии, начиная с первого, нужно сложить, чтобы их сумма была равна 3069?

Найдем характеристики геометрической профессии. Используя формулу n-го члена, запишем условия задач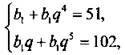и: или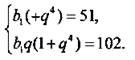

Разделив второе уравнение на первое, получим:

Из первого уравнения найдем:

Предположим, что сложили n членов профессии и получили сумму

По условию такая сумма равна 3069. Имеем уравнение: 3(2n - 1) = 3069, или 2n - 1 = 1023, или 2n = 1024 = 210, откуда n = 10. Итак, нужно сложить десять первых членов профессии.

Пример 4

Решить уравнение 1 + 2 + 4 + 8 + ...+ x = 255.

В левой части уравнения находится сумма геометрической прогрессии с первым членом 1, знаменателем 2. Пусть число слагаемых равно n. Тогда эта сумма равна: отсюда: 2n = 256 = 28. Так как х является n-м членом прогрессии, то х = 1 · 2n-1 = 28-1 = 27 = 128.

Очень распространен круг задач, где для суммирования чисел и алгебраических выражений используется сумма геометрической прогрессии.

Пример 5

Найти сумму:

Возведем в квадрат слагаемые этой суммы и получим: Перейдем к отрицательным показателям степени и сгруппируем слагаемые, входящие в S: Каждая из трех скобок содержит по n слагаемых. Причем первая скобка содержит сумму геометрической прогрессии с первым членом х2 и знаменателем х2; вторая - сумму геометрической прогрессии с первым членом х-2 и знаменателем х-2; третья - сумму чисел 2. Учитывая это, получим:

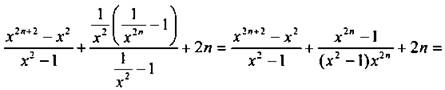
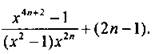
Пример 6

Найти сумму:

Умножим и разделим искомую сумму на 9: 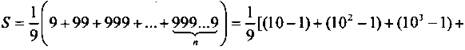Затем сгруппируем слагаемые суммы: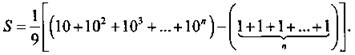

Первая скобка представляет собой сумму геометрической прогрессии с первым членом 10 и знаменателем 10. Учитывая это, получим: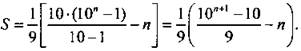

Пример 7

При любом n сумма Sn членов некоторой последовательности (bn) находится по формуле Sn = 6 · 3n - 2. Докажите, что эта последовательность не является геометрической прогрессией, и найдите пять первых членов этой последовательности.

Как в примере 3, воспользуемся определением геометрической прогрессии. Найдем сначала формулу n-го члена данной последовательности (bn). Очевидно, что

Найдем отношение двух соседних членов этой последовательности: откуда bn = bn-1 · 3. Казалось бы, данная последовательность является геометрической прогрессией со знаменателем 3. Однако выражение для bn = Sn - Sn-1 справедливо только для n ≥ 2 (т. к. при n = 1 величина Sn-1 не существует). Поэтому выражение для будет справедливо уже при n ≥ 3 (т. к. при n = 2 величина bn-1 не описывается полученной формулой).

Итак, из приведенных рассуждений видно, что при n ≥ 2 члены последовательности описываются соотношением bn = 12 · 3n-1, и по этой формуле находим: b2 = 36, b3 = 108, b4 = 324, а5 = 972. Легко проверить, что Для нахождения b1 учтем, что при n = 1 сумма Sn состоит всего из одного члена b1 и b1 = S1 = 6 · 3 – 2 = 16. Видно, что

Таким образом, последовательность не является геометрической прогрессией. Первые пять ее членов, соответственно, равны: 16; 36; 108; 324; 972.

Если |q| < 1, то прогрессия называется бесконечно убывающей геометрической прогрессией. Для нее, разумеется, как и для любой геометрической прогрессии, справедливы свойства и формулы, приведенные выше. Кроме того, можно вычислить сумму бесконечного числа членов такой прогрессии по формуле

Пример 8

Сумма бесконечно убывающей геометрической прогрессии равна 4, а сумма кубов ее членов равна 192. Найти эту прогрессию.

Пусть дана прогрессия Тогда ее сумма Кубы членов данной прогрессии: также образуют геометрическую прогрессию с первым членом b13 и знаменателем q3. Так как при |q| < 1 величина |q3| = |g|3 < 1, то эта прогрессия также бесконечно убывающая и ее сумма: Получаем систему нелинейных уравнений: 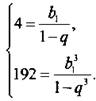Для решения этой системы возведем первое уравнение в куб: 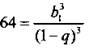и разделим второе уравнение системы на полученное уравнение: или 2q2 + 5q + 2 = 0. Корни этого уравнения q = -1/2 и q = -2 (не подходит, т. к. прогрессия бесконечно убывающая и |q| < 1). Теперь из первого уравнения находим

Понятие бесконечно убывающей геометрической прогрессии позволяет обращать десятичные бесконечные периодические дроби в обыкновенные.

Пример 9

Обратить десятичную дробь 0,(17) в обыкновенную.

Запишем дробь в виде Таким образом, число 0,(17) является суммой бесконечно убывающей геометрической прогрессии, у которой b1 = 7/100 и q = 1/100.

Эта сумма равна: Итак, 0,(17) = 17/99.

Заметим, что возможно и другое решение. Пусть дробь 0,(17) = х, т. е. х = 0,1717... . Учитывая, что период этой дроби содержит две цифры, умножим величину х на 100: 100х = 17,1717....

Вычтем из 100х величину х и получим: 100х - х = 17,1717 - 0,1717 = 17.

Для нахождения х имеем линейное уравнение 99х = 17, откуда х = 17/99.

Пример 10

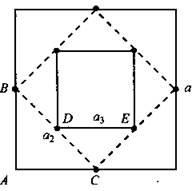
Сторона квадрата равна а. Середины сторон этого квадрата соединим отрезками. Получился новый квадрат. С этим квадратом поступили так же, как и с данным, и т. д. Найти суммы сторон, периметров и площадей всех этих квадратов.

Обозначим стороны этих квадратов (начиная с данного): а, а2, а3, ... . Рассмотрим прямоугольный равнобедренный ΔABC:

Запишем для него теорему Пифагора: ВС2 = АВ2 + АС2, или 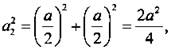откуда Аналогично из прямоугольного ΔDEC находим: 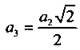и т. д.

Таким образом, стороны квадратов образуют бесконечно убывающую геометрическую прогрессию: 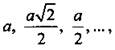у которой первый член а и знаменатель

Найдем ее сумму: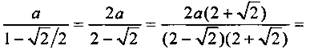

Так как периметр квадрата 4а, то периметры приведенных квадратов также образуют бесконечно убывающую геометрическую прогрессию с первым членом 4а и знаменателем поэтому ее сумма

Площадь квадрата а2 и площади квадратов: образуют бесконечно убывающую геометрическую прогрессию с первым членом а2 и знаменателем 1/2, поэтому сумма площадей равна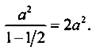

Итак, сумма сторон: периметров: площадей: 2а2.

IV. Контрольные вопросы

1. Формула суммы первых n членов геометрической прогрессии.

2. Сумма членов бесконечно убывающей геометрической прогрессии.

V. Задание на уроке

№ 648 (а); 649 (б, в); 650 (а); 651 (б); 652 (а, г); 653; 655.

VI. Задание на дом

№ 648 (б); 649 (а, г); 650 (б); 651 (а); 652 (в, д); 654; 657.

VII. Подведение итогов урока