Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Метод математической индукции (факультативное занятие) - Геометрическая прогрессия - Арифметическая и геометрическая прогрессии
Цель: рассмотреть новый способ доказательства утверждений.
Ход урока
I. Сообщение темы и цели урока
II. Ответы на вопросы по домашнему заданию
III. Изучение нового материала
Для доказательства утверждений, зависящих от натурального числа и, используют метод математической индукции. Для доказательства применяется следующая схема:
1. Проверяют справедливость утверждения при n = 1 (или при первом допустимом по условию задачи значении n).
2. Предполагают, что при произвольном значении n = k утверждение верно.
3. Доказывают, что при следующем значении n = k + 1 утверждение верно, используя предыдущий пункт 2.
Метод математической индукции аксиоматический и принимается без доказательства. Несмотря на его непривычность, нетрудно понять, как он «работает». Мы проверили доказываемое утверждение при некотором конкретном n (например, при n = 1). Так как было доказано, что если утверждение верно при n = k, то оно верно и при n = k + 1. Это означает, что утверждение будет верно и при n = 1 + 1 = 2. Так как оно верно при n = 2 и было доказано, что утверждение справедливо для n = k + 1, то оно верно при n = 2 + 1 = 3 и т. д. Таким образом, утверждение справедливо при всех натуральных значениях n.
Основная идея метода математической индукции состоит в доказательстве перехода: n = k → n = k + 1. Этот переход позволяет «зациклить» процесс: при n = 1 легко проверить утверждение, в силу перехода n = k → n = k + 1 оно верно и при n = 1 + 1 = 2. Так как оно верно при n = 2, в силу того же перехода оно верно и для n = 2 + 1 = 3 и т. д.
Пример 1
Докажем, что при всех натуральных п выражение А(n) = n(n2 + 5) без остатка делится на 6.
Используем приведенную схему доказательства:
1. При n = 1 выражение А(1) = 1 · (12 + 5) = 6 и делится на 6.
2. Предположим, что при n = k выражение А(k) = k(k2 + 5) = k3 + 5k делится без остатка на 6, т. е. k3 + 5k = 6р (где р - натуральное число).
3. При n = k + 1 получаем выражение А(k +1) = (k + 1)3 + 5(k + 1) = k3 + 3k2 + 8k+ 6. Выделим в этом выражении часть, которая согласно пункту 2 делится на 6: А(k + 1) = (k3 + 5k) + (3k2 + 3k + 6) = 6р + (3k2 + 3k + 6). Нужно доказать, что выражение 3k2 + 3k + 6 делится на 6. Для этого достаточно, чтобы выражение 3k2 + 3k = 3k(k + 1) делилось на 6 или k(k + 1) делилось на 2. Но величина k(k + 1) является произведением двух соседних натуральных чисел k т k + 1. Разумеется, одно из них будет четным.
Пример 2
Докажем, что при любом натуральном и выражение А(n) = 4n + 15n - 1 кратно 9.
Используем стандартную схему доказательства:
1. При n = 1 выражение A(1) = 41 + 15 · 1 - 1 = 18 кратно 9.
2. Предположим, что при n = k выражение А(k) = 4k + 15k - 1 кратно 9, т. е. 4k + 15k - 1 = 9р (где р - натуральное число).
3. При n = k + 1 надо доказать, что выражение А(k +1) = 4k+1 + 15(k + 1) - 1 делится на 9. Для доказательства можно использовать два способа.
1-й способ. Поступим, как и в примере 1, т. е. выделим в выражении А(k + 1) часть А(k), которая делится на 9. Для этого преобразуем выражение А(k + 1) к виду А(k +1) = 4k+1 + 15k + 14 = 4(4k + 15k - 1) – 45k + 18 = 4 А(k) + 9(2 – 5k).
Видно, что выражение А(k + 1) является суммой двух слагаемых, каждое из которых делится на 9.
Сложность этого способа состоит в умении в выражении А(k + 1) выделить часть А(k), т. е. догадаться до преобразования 4k+1 + 15k + 14 = 4(4k + 15k - 1) – 45k + 18.
Поэтому рассмотрим другой способ, лишенный такого недостатка.
2-й способ. Из выражения 4k + 15k - 1 = 9р (пункт 2) найдем 4k = 9р + 1 – 15k и подставим в выражение А(k +1) = 4k+1 + 15k + 14 = 4(9p + 1 – 15k) + 15k + 14 = 36p + 18 – 45k. Видно, что выражение A(k + 1) состоит из трех слагаемых, каждое из которых делится на. 9.
Связь между пунктами 2 и 3 была обеспечена за счет того, что в пункте 2 была найдена величина 4k и подставлена в выражение пункта 3.
Заметим, что если на число п накладываются по условию задачи ограничения, то необходимо ввести новое натуральное число т и свести задачу к старой схеме.
Пример 3
Докажем, что при четных неотрицательных числах n выражение А(n) = 52n+1 +3n+1 кратно 8.
Так как n четное и неотрицательное число, то его можно записать в виде n = 2m - 2 (где m - любое натуральное число). Заменив в А(n) число на 2m - 2, переформулируем задачу: докажем, что при любом натуральном значении m выражение ![]() кратно 8. Далее применима стандартная схема доказательства:
кратно 8. Далее применима стандартная схема доказательства:
1. При m = 1 выражение А(1) = 51 + 31 = 8 кратно 8.
2. Предположим, что при m = k выражение А(k) = 54k-3 + 32k-1 кратно 8, т. е. 54k-3 + 32k-1 = 8р (где р - натуральное число). Выразим из этого равенства 54k-3 = 8р – 32k-1.
3. При m = k + 1 получаем выражение ![]()
![]()
![]()
![]()
Видно, что это выражение делится на 8.
Заметим, что при попытке доказать ложное утверждение метод математической индукции приведет к противоречию.
Пример 4
Докажем, что при всех натуральных n выражение А(n) = n2 + 7 кратно 4.
Разумеется, это утверждение ложное, т. к., например, при n = 2 получаем: А(2) = 22 + 7 = 11 - число, которое не делится на 4. Тем не менее попробуем применить метод математической индукции:
1. При n = 1 получаем число A(1) = 12 + 7 = 8, которое кратно 4.
2. Предположим, что при n = k число А(k) = k2 + 7 делится на 4.
3. При n = k + 1 получаем выражение А(k + 1) = (k + 1)2 + 7 = k2 + 2k + 1 + 7 = (k2 + 7) + (2k + 1).
Согласно пункту 2 выражение k2 + 7 кратно 4. Выражение 2k + 1 при всех натуральных числах k является нечетным числом и не делится на 4. Таким образом, получаем противоречие с условием задачи.
Метод математической индукции пригоден не только для доказательства утверждений, связанных с делимостью выражений, но и при доказательстве теорем, тождеств, неравенств, в геометрических задачах и т. д. Поэтому рассмотрим еще некоторые случаи применения метода математической индукции.
Пример 5
Докажем, что при любом натуральном n сумма ![]()
![]() равна
равна ![]()
Заметим, что в сумму входит n дробей. Используем метод математической индукции:
1. При n = 1 сумма состоит из одной дроби. Получаем верное равенство 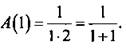
2. Предположим, что при n = k равенство выполняется: ![]()
![]()
3. При n = k + 1 получаем выражение ![]()
![]()
![]()
Видно, что полученное выражение описывается формулой ![]() при n = k + 1.
при n = k + 1.
Пример 6
При a > -1 и любом натуральном n докажем неравенство ![]()
1. При n = 1 имеем верное неравенство ![]()
2. Предположим, что при n = k неравенство выполнено, т. е. ![]()
3. При n = k + 1 надо доказать неравенство ![]()
Для этого обе части неравенства (пункт 2) ![]() умножим на положительное число 1 + а. Получаем неравенство того же знака:
умножим на положительное число 1 + а. Получаем неравенство того же знака: ![]() или
или ![]()
Так как число kа2 неотрицательное, то справедливо неравенство ![]()
Тогда верно неравенство ![]()
Пример 7
Докажем, что n-угольник имеет ![]() диагоналей.
диагоналей.
Очевидно, что n ≥ 3. Используем стандартную схему:
1. При n = 3 получаем А(3) = 0, т. е. треугольник не имеет диагоналей, и это верно.
2. Предположим, что при n = k многоугольник имеет ![]() диагоналей.
диагоналей.
3. При n = k + 1 получаем (k + 1)-угольник. Очевидно, что вершину с номером k + 1 можно соединить с остальными вершинами к отрезками. Из этих отрезков один отрезок является стороной многоугольника, а k - 1 отрезок - его диагоналями. Таким образом, к ![]() диагоналям k-угольника добавляются еще k - 1 диагонали. Всего получаем:
диагоналям k-угольника добавляются еще k - 1 диагонали. Всего получаем: ![]()
![]()
Имеем значение выражения А(n) при n = k + 1.
Подчеркнем еще раз универсальность и удобство метода математической индукции.
IV. Контрольные вопросы
1. Схема доказательства методом математической индукции.
2. Основной смысл метода математической индукции.
V. Задание на уроке
№ 662; 665; 667; 669 (а).
VI. Задание на дом
№ 663; 666; 668; 669 (б).
VII. Творческие задания
Методом математической индукции докажите, что при любом натуральном и справедливо утверждение.

11) 4n + 15n - 7 делится на 9;
12) n3 + 3n2 + 5n делится на 3;
13) 10n + 18n - 28 делится на 27;
14) n7 - n делится на 42;
15) 72n - 42n делится на 33;
16) 11n+2 + 122n+1 делится на 133.
VIII. Подведение итогов урока