Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Итоги контрольной работы - урок 4 - Геометрическая прогрессия - Арифметическая и геометрическая прогрессии
Цель: сообщить результаты работы, рассмотреть наиболее типичные ошибки, разобрать трудные задачи.
Ход урока
I. Сообщение темы и цели урока
II. Итоги контрольной работы
III. Ответы и решени.
Ответы
Вариант 1
1. Ответ: 38.
2. Ответ: 186.
3. Ответ: 1455.
4. Ответ: -4.
5. Ответ: 242.
6. Ответ: 8/33.
Вариант 2
1. Ответ: 63.
2. Ответ: -20.
3. Ответ: 2300.
4. Ответ: 1/3.
5. Ответ: 45.
6. Ответ: 4/11.
Вариант 3
1. Ответ: 2.
2. Ответ: a1 = -2 и d = 9.
3. Ответ: 1/3.
4. Ответ: 189 и 63.
5. Ответ: 12/55.
6. Ответ: 163.
Вариант 4
1. Ответ: 2.
2. Ответ: a1 = -8 и d = 11.
3. Ответ: 1/2.
4. Ответ: 728 и 364.
5. Ответ: 29/55.
6. Ответ: 475.
Решения
Вариант 5
1. Сгруппируем слагаемые и используем формулу разности квадратов. Получаем:

Учтено, что 25 слагаемых 99, 95, ..., 3 являются членами арифметической прогрессии.
Ответ: 1275.
2. Данные числа образуют арифметическую прогрессию (аn), в которой а1 = х + 1 и d = 4. Тогда n-й член прогрессии аn = х + 1 + 4(n - 1) = х + 4n - 3.
Найдем число слагаемых в сумме. Получаем уравнение х + 157 = х + 4n - 3, откуда n = 40. Запишем данную сумму: ![]()
Ответ: 40.
3. Запишем условия задачи: 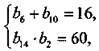 или
или  или
или 
Решения этой симметричной системы уравнений: b6 = 6, b10 = 10 и b6 = 10, b10 = 6.
Ответ: b6 = 6, b10 = 10 и b6 = 10, b10 = 6.
4. По условиям задачи получаем симметричную систему уравнений  или
или 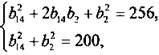 откуда b14b2 = 28.
откуда b14b2 = 28.
Запишем это равенство в виде ![]() или b82 = 28 и
или b82 = 28 и ![]()
Ответ: ![]()
5. Так как числа а, b, с образуют геометрическую прогрессию, то b = aq и c = aq2.
Тогда числа a + b, b + с и а + с образуют арифметическую прогрессию.
Запишем ее характеристическое свойство: 2(b + с) = (а + b) + (а + с), или 0 = 2а - b - с, или 0 = 2a – aq - aq2, или 0 = q2 + q - 2, откуда q = -2 и q = 1 (не подходит, т. к. числа а, b, с- разные.).
Ответ: -2.
6. Запишем рекуррентную формулу ![]() (где a1 = 2 и а2 = 1) для: n = 3:
(где a1 = 2 и а2 = 1) для: n = 3: ![]()
![]()
![]()
Ответ: -13.
Вариант 6
1. Сгруппируем слагаемые и используем формулу разности квадратов. Получаем:
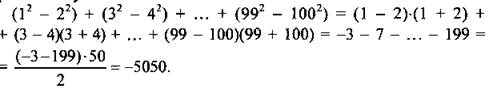
Учтено, что 50 слагаемых -3, -7, ..., -199 являются членами арифметической прогрессии.
Ответ: -5050.
2. Данные числа образуют арифметическую прогрессию (an), в которой a1 = x + 3 и d = 5. Тогда n-й член прогрессии ![]()
Найдем число слагаемых в сумме. Получаем уравнение х + 248 = х + 5n - 2, откуда n = 50.
Запишем данную сумму: ![]() или 2х + 251 = 249, откуда х = -1.
или 2х + 251 = 249, откуда х = -1.
Ответ: -1.
3. Запишем условия задачи:  или
или 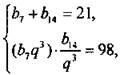 или
или 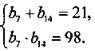
Решения этой симметричной системы уравнений: b7 = 7, b14 = 14 и b7 = 14, b14 = 7.
Ответ: b7 = 7, b14 = 14 и b7 = 14, b14 = 7.
4. По условиям задачи получаем симметричную систему уравнений  или
или  откуда b11b3 = 33.
откуда b11b3 = 33.
Запишем это равенство в виде ![]() или b72 = 33 и
или b72 = 33 и ![]()
Ответ: ![]()
5. Так как числа а, b, с образуют геометрическую прогрессию, то b = aq и с = аq2. Тогда числа а - b, b + с и b - с образуют арифметическую прогрессию.
Запишем ее характеристическое свойство: 2(b + с) = (a - b) + (b - c), или 0 = а – 2b - с, или 0 = а – 2aq - 3aq2, или 0 = 3q2 + 2q - 1, откуда q = -1 (не подходит, т. к. числа а, b, с - положительные) и q = 1/3.
Ответ: 1/3.
6. Запишем рекуррентную формулу ![]() (где a1 = 2 и a2 = 1) для: n = 3:
(где a1 = 2 и a2 = 1) для: n = 3: ![]()
![]()
![]()
Ответ: -10.