Уравнения и системы уравнений - Повторение курса 7-9 классов

Цель: повторить основные способы решения уравнений и систем уравнений.

Ход урока

I. Сообщение темы и цели урока

II. Контроль усвоения материала (самостоятельная работа.

Вариант 1

1. Найдите значение выражения.

2. Упростите выражение.

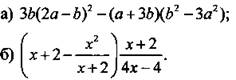
Вариант 2

1. Найдите значение выражения.

2. Упростите выражение.

III. Повторение пройденного материала

Уравнения

Корнем уравнения с одной переменной называют такое значение переменной, при котором уравнение обращается в верное равенство.

Решить уравнение - значит найти все его корни или доказать, что корней нет.

Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными.

Уравнения, не имеющие корней, также считают равносильными.

Уравнения будут равносильными, если:

1) в уравнении перенести слагаемое из одной части в другую, изменив его знак;

2) обе части уравнения умножить или разделить на одно и то же отличное от нуля число.

Уравнением n-й степени (n ≥ 1) называют уравнение вида Рn(х) = 0, где Рn(х) - многочлен n-й степени.

При n = 1 имеем линейное уравнение ах - b = 0.

Для а ≠ 0 такое уравнение имеет единственный корень х = b/a.

Для а = 0 и b ≠ 0 уравнение не имеет корней.

Для а = 0 и b = 0 корнем уравнения является любое число х.

При n = 2 имеем квадратное уравнение ах2 + bх + с = 0, где а ≠ 0.

Если хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением и решают разложением его левой части на множители.

Дискриминантом квадратного уравнения ах2 + bх + с = 0 называют выражение D = b2 - 4ас.

Если D > 0, то уравнение имеет два различных корня 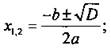если D = 0 - один корень (или два равных корня) х = -b/2a; если D < 0 уравнение корней не имеет.

Для квадратного уравнения выполняется теорема Виета: если x1 и х2 - корни уравнения ах2 + bх + с = 0, то сумма корней х1 + х2 = -b/a и произведение корней х1х2 = c/a.

При n ≥ 3 имеем уравнение высокой степени. Такие уравнения решают или разложением левой части на множители, или введением новой переменной.

При решении дробных рациональных уравнений используют следующий алгоритм:

1) находят общий знаменатель дробей, входящих в уравнение;

2) умножают обе части уравнения на общий знаменатель;

3) решают получившееся целое уравнение;

4) исключают из его корней те, которые обращают в нуль общий знаменатель.

Системы уравнений

Решением уравнения с двумя переменными называют пару значений переменных, которые обращают это уравнение в верное равенство.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения, не имеющие решений, также считают равносильными.

Каждое решение (х; у) уравнения с двумя переменными можно изобразить точкой с координатами х и у на координатной плоскости. Все такие точки образуют график уравнения.

Линейным уравнением с двумя переменными х и у называют уравнение вида ах + by = с. Графиком такого уравнения является прямая линия.

Системой двух линейных уравнений с двумя переменными х и у называют систему вида Такая система имеет единственное решение при не имеет решения при и имеет бесконечное множество решений при

Для решения систем уравнений с двумя переменными используют:

а) способ подстановки;

б) способ сложения;

в) способ замены переменной;

г) графический способ.

При решении систем двух нелинейных уравнений тем или иным способом получают линейное уравнение и далее используют способ подстановки.

IV. Задание на уроке

№ 925 (а, в); 926; 935 (а, в, е); 937; 940 (б, е); 943; 957 (а, г); 958 (б); 967; 972 (а, б); 973 (в); 974 (а, в); 981; 985; 993.

V. Задание на дом

№ 925 (б, г); 927; 935 (б, г, д); 938; 940 (в, д); 944; 957 (б, в); 958 (а); 969; 972 (в, г); 973 (д); 974 (б, г); 982; 986; 994.

VI. Подведение итогов урока