Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Задачи
Тригонометрические неравенства
Решите неравенства:
14.1. |sin x| > |cos x|.
14.2. 1 − sin x + cos x < 0.
14.3. sin x − З cos x < 0.
14.4. 2 cos 2х + sin 2х > tg x.
14.5. cos x tg 2х ≤ 0.
14.6. 6 + cos 2х + 13 cos x ≥ |5 − 2 cos 2х − 6 sin² x − З cos x|.
14.7. Найдите решения неравенства
sin 2х > √2 sin² x + (2 − √2) cos² x,
лежащие в интервале (0, 2π).
14.8. При каких значениях α, 0 ≤ α ≤ π, уравнение
2х² − 2(2 cos α − 1)x + 2 cos² α − 5 cos α + 2 = 0 имеет различные действительные корни? Исследуйте знаки корней.
Решите неравенства:
14.9.
![]()
14.10.
![]()
14.11.
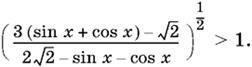
14.12. tg x tg 3x < −1.
14.13.
![]()
14.14. Найдите все значения x из интервала 0 < x < π, удовлетворяющие неравенству
![]()
14.15. Докажите, что при любом а имеет место неравенство
4 sin 3α + 5 ≥ 4 cos 2α + 5 sin α.
14.16. Решите неравенство
a² sin² x ≤ sin² 3x, а > 0.
14.17. При каких значениях x и у выражение
(2 cos t + ½ cos x cos у ) cos x cos у + 1 + cos x − cos у + cos 2t
положительно при всех значениях t? Укажите, где на координатной плоскости расположены точки (x, у), удовлетворяющие этому условию.