Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Тригонометрические уравнения и системы
13.1. Так как √2 sin (x + π/4) = sin x + cos x, то
1 + sin 2x + 2 cos 3x sin x + 2 cos 3x cos x = 2 sin x + 2 cos 3x + cos 2x.
Объединим одночлены, содержащие cos 3x и все оставшиеся одночлены:
2 cos 3x (sin x + cos x − 1) + 2 sin x (sin x + cos x − 1) = 0.
Получим уравнение
(sin x + cos x − 1)(cos 3x + sin x) = 0.
Если sin x + cos x = 1, т. е. (x − π/4) = 1/√2 , то
x = nπ/2 − π/8 и x = nπ + π/4.
Ответ. 2nπ; 2nπ + π/2; nπ/2 − π/8; nπ + π/4.
13.2. Данное уравнение можно преобразовать так:
![]()
или
![]()
Последнее уравнение равносильно системе
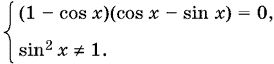
Решая уравнение этой системы, найдем
cos x = 1, откуда x = 2kπ,
cos x = sin x, tg x = 1, откуда x = π/4 + kπ.
Так как при x = 2kπ и x = π/4 + kπ условие sin² x ≠ 1 выполняется, то найденные значения x являются корнями данного уравнения.
Ответ. x = 2kπ; x = π/4 + kπ.
13.3. Поскольку
![]()
мы приходим к уравнению
![]()
Левая и правая части этого уравнения содержат общий множитель 1 − cos x/1 − sin x. Поэтому уравнение можно записать в виде
![]()
Первые корни получаем из уравнения cos x = 1, откуда x = 2kπ.
Остальные корни найдем, приведя к общему знаменателю дроби, стоящие в скобке, и выполнив вычитание. Получим уравнение
![]()
Числитель легко разложить на множители, если сгруппировать однородные члены:
(sin² x − cos² x) + sin x cos x (sin x − cos x) = (sin x − cos x)(sin x + sin x cos x + cos x).
Знаменатель можно отбросить, так как при cos x = 0 ни одна из скобок в разложении числителя не обращается в нуль. Заботиться о том, чтобы 1 + sin x + sin² x не обращалось в нуль, не нужно, так как это выражение всегда положительно.
Если sin x − cos x = 0, то tg x = 1, откуда x = π/4 + kπ.
Остается решить уравнение
sin x + sin x cos x + cos x = 0.
Мы знаем, что (sin x + cos x)² = 1 + 2 sin x cos x. Отсюда
![]()
Сделав такую замену в оставшемся уравнении, получим квадратное уравнение относительно y = sin x + cos x
y² + 2y − 1 = 0.
Корни этого уравнения
y1,2 = −1 ± √2.
Записав sin x + cos x в виде √2 cos (x − π/4), мы убедимся, что корень y1 = −1 − √2 является посторонним. Остается
cos (x − π/4) = 1 − 1/√2,
откуда
x = 2kπ ± arccos (1 − 1/√2) + π/4.
Ответ. 2kπ; π/4 + kπ; 2kπ ± arccos (1 − 1/√2) + π/4.
13.4. Данное уравнение эквивалентно системе

Преобразуя левую и правую части уравнения в сумму тригонометрических функций, мы получим уравнение
cos 9x = 0, откуда x = π/18(2n + 1).
Из найденных значений x нужно выбрать те, при которых
cos 2x cos 7x ≠ 0, т. е. cos 5x + cos 9x ≠ 0.
Так как речь идет о значениях неизвестного, при которых cos 9 x = 0, то остается потребовать, чтобы cos 5x ≠ 0, т. е. 5 · π/18(2n + 1) ≠ π/2(2k + 1), откуда 5(2n + 1)/9 ≠ 2k + 1. Число 5(2n + 1)/9 не может быть четным, так как в его числителе лишь нечетные множители.
Оно будет целым, когда = 2n + 1/9 = 2n + 1, т. е. при n = 9m + 4.
Следовательно, корнями уравнения являются числа x = π/18(2n + 1) при n ≠ 9m + 4.
Ответ. π/18(2m ± 1); π/18(18m ± 3); π/18(18m ± 5); π/18(18m ± 7).
13.5. Если запишем данное уравнение в виде
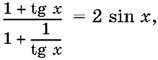
то получим равносильное уравнение. Однако дальнейшие преобразования заставляют нас ввести ограничения:
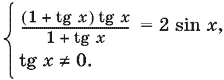
Далее
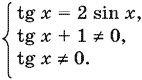
Когда tg x ≠ 0, то и sin x ≠ 0. Это означает, что первое уравнение можно переписать в виде 1/cos x = 2, откуда cos x = ½, что обеспечивает выполнение всех ограничений.
Ответ. 2nπ ± π/3.
13.6. Прибавив к обеим частям уравнения tg 3x, получим
3(tg 3x − tg 2x) = tg 3x (1 + tg² 2x),
или
![]()
Последнее уравнение эквивалентно системе
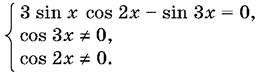
Решим первое уравнение. Для этого представим произведение sin x cos 2x в виде разности синусов. После приведения подобных членов получим
sin 3x = 3 sin x.
Воспользовавшись формулой синуса тройного угла, придем к уравнению
sin x (3 − 4 sin² x) = 3 sin x, или sin³ x = 0,
откуда x = πk.
Легко проверить, что при x = πk ни cos 2x, ни cos 3x в нуль не обращаются.
Ответ. πk.
13.7. Преобразуем уравнение следующим образом:
(sin x + cos x)(1 − sin xcos x) + 1/√2 sin 2xsin (x + π/4) = sin (π/2 − x) + sin 3x.
Так как sin x + cos x = √2 sin (π/4 + x), то придем к уравнению
sin (π/4 + x) = √2 sin (π/4 + x ) cos (π/4 − 2x).
Если sin (π/4 + x) = 0, то x1 = π/4(4n − 1). Остается
√2 cos (π/4 − 2x) = 1,
откуда
x2 = nπ, x3 = π/4(4n + 1).
Серии чисел x1, = π/4(4n − 1) и x3 = π/4(4n + 1) можно объединить: x1 = π/4(2n + 1).
Ответ. π/4(2n + 1); nπ.
13.8. Перепишем уравнение следующим образом:
4(tg 4x − tg 3x) = tg 2x (1 + tg 3x tg 4x).
Приведем выражения в скобках к виду, удобному для логарифмирования:
![]()
Уравнение равносильно системе
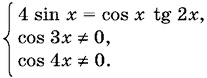
Так как cos x = 0 не удовлетворяет уравнению, то его можно переписать так:
4 tg x = tg 2x, или 2 tg x = tg x/1 − tg² x.
Мы воспользовались неабсолютным тождеством, которое исключает из области определения те значения x, при которых tg x не существует. Однако tg x входил в предыдущее уравнение, а потому существует, и потеря корней произойти не может. Из последнего уравнения, если tg x = 0, получаем x = nπ.
Если tg x ≠ 0, то 2 − 2 tg² x = 1, tg x = ±1/√2. Так как cos 3x и cos 4x не обращаются при этом в нуль, то можно написать ответ.
Ответ. nπ; nπ ± arctg 1/√2.
13.9. Уравнение можно переписать так:
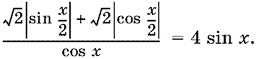
Поскольку 0 < x < 2π, то 0 < x/2 < π и sin x/2 > 0. Однако cos x/2 в этом интервале меняет знак, и нам придется разбить интервал на два: 0 < x ≤ π и π < x < 2π.
Если 0 < x ≤ π, получим уравнение
√2/2 sin x/2 + √2/2 cos x/2 = sin 2x,
y которого может появиться лишь один посторонний корень при cos x = 0. Перепишем последнее уравнение так:
sin (x/2 + π/4) = sin 2x,
и найдем его корни из интервала 0 < x ≤ π: x1 = π/6, x2 = 3π/10. Если π < x < 2π, придем к уравнению
√2/2 sin x/2 − √2/2 cos x/2 = sin 2x или sin (x/2 − π/4) = sin 2x,
которое даст нам еще два корня: x3 = 7π/6, x4 = 13/10 π. Очевидно, что для полученных углов cos x ≠ 0.
Ответ. π/6; 3π/10; 7π/6; 13π/10.
13.10. Перенеся sin α в левую часть, запишем уравнение в виде
2 sin x/2 cos x − 2α/2 = 2 sin x/2 cos x/2,
или
sin x/2 (cos x − 2α/2 − cos x/2) = 0.
Если sin x/2 = 0, то x = 2nπ при любом α. Если cos x − 2α/2 = cos x/2, то либо x − 2α/2 + x/2 = 2nπ, откуда x = 2nπ + α, либо x − 2α/2 − x/2 = 2nπ, откуда α = 2nπ.
Ответ. При любом α: 2nπ, 2nπ + α; при α = 2nπ: x − любое.
13.11. Уравнение равносильно совокупности двух уравнений
cos 2x = sin² x − a, cos 2x = a − sin² x.
Понизим степень в правой части каждого уравнения и найдем
cos 2x = 1 − 2a/3, cos 2x = 2a − 1.
Первое уравнение имеет решение, если
−1 ≤ 1 − 2a/3 ≤ 1, т. е. −1 ≤ a ≤ 2.
Второе уравнение имеет решение, если −1 ≤ 2a − 1 ≤ 1, т. е. 0 ≤ a ≤ 1. Данное в условии уравнение при −1 ≤ a ≤ 2 имеет решения
x = πn ± ½ arccos 1 − 2a/3,
а при 0 ≤ a ≤ 1 решения
x = πn ± ½ arccos (1 − 2a).
Так как
0 ≤ ½ arccos 1 − 2a/3 ≤ π/4 и 0 ≤ ½ arccos (1 − 2a) ≤ π/2,
то легко найти решения нашего уравнения, которые попадут в интервал 0 ≤ x ≤ 2π.
Ответ. ½ arccos 1 − 2a/3; π ± ½ arccos 1 − 2a/3; 2π − ½ arccos 1 − 2a/3 (существуют при −1 ≤ a ≤ 2);
½ arccos (1 − 2a); π ± ½ arccos (1 − 2a); 2π − ½ arccos (1 − 2a) (существуют при 0 ≤ a ≤ 1).
13.12. Преобразуем подкоренное выражение следующим образом:
sec² (17 + 8 sin x − 16 cos² x) = sec² x (1 + 8 sin x + 16 sin² x) = sec² x (1 + 4 sin x)².
Данное уравнение принимает вид
|1 + 4 sin x|/|cos x| = 2 tg x (1 + 4 sin x).
Если 1 + 4 sin x = 0, то x = nπ + (−1)n + 1 arcsin ¼. Это — корни нашего уравнения, так как cos x ≠ 0 и tg x существует.
Если 1 + 4 sin x ≠ 0, то придется рассмотреть два случая, зависящих от знака этого выражения.
Пусть 1 + 4 sin x > 0, т. е. sin x > −¼. Тогда придем к уравнению
1/|cos x| = 2 tg x, или 2 tg x|cos x| = 1,
которое равносильно совокупности систем

Вторая система не имеет решений при sin x > −¼. Решение первой: x = π/6 + 2nπ.
Пусть, наконец, 1 + 4 sin x < 0, т. е. sin x < −¼. Уравнение
2 tg x |cos x| = −1,
к которому мы приходим в этом случае, равносильно такой совокупности систем:
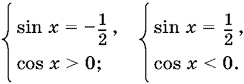
Вторая система не имеет решений при sin x < −¼, а первая дает нам x = −π/6 + 2nπ.
Ответ. nπ + (−1)n + 1 arcsin ¼; ±π/6 + 2nπ.
13.13. Поскольку tg x + sin x = tg x (1 + cos x) = 2 tg x cos² x/2, а tg x − sin x = 2 tg x sin² x/2, данное уравнение можно записать в виде
√2 tg½ x(|cos x/2| + |sin x/2| − √2 cos x) = 0.
Первые решения получим при tg x = 0; x = kπ. Остальные решения нам доставят корни уравнения
|cos x/2| + |sin x/2| = √2 cos x,
при которых tg x > 0 (случай tg x = 0 уже исследован). Решим вначале последнее уравнение, а затем исключим те решения, которые не удовлетворяют неравенству tg x > 0. Возведем это уравнение в квадрат и, чтобы не нарушить равносильности, добавим ограничение cos x ≥ 0. Получим систему
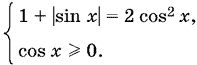
Так как одновременно tg x > 0 и cos x > 0, то sin x > 0. Поэтому
|sin x| = sin x.
Приходим к уравнению
2sin² x + sin x − 1 = 0.
Решая его, найдем
|sin x| = −1 ± 3/4.
Так как |sin x| ≥ 0, то остается решить уравнение
|sin x| = ½,
корнями которого будут числа
x = π/6 + 2πk, x = 5π/6 + 2πk.
Остается вспомнить, что tg x > 0.
Ответ. kπ, π/6 + 2kπ.
13.14. При замене 1/sin 4x на
![]()
можно ожидать потери корней, при которых tg 2x не существует, или, что то же самое, cos 2x = 0. Однако при cos 2x = 0 обращается в нуль и sin 4x, т. е. потери корней не произойдет.
Так как в левую часть уравнения
ctg 2x + 3 tg 3x = 2 tg x + (1 + tg² 2x)1/tg 2x
входит ctg 2x, то, заменив 1/tg 2x на ctg 2x и раскрыв скобки, мы уничтожим в правой и левой частях ctg 2x. Замена 1/tg 2x = ctg 2x грозит лишь приобретением корней, при которых tg 2x не существует, т. е. безопасна, так как tg 2x остается в уравнении. Когда происходит уничтожение одинаковых слагаемых ctg 2x, то нужно добавить к уравнению
3 tg 3x = 2 tg x + tg 2x,
условие
ctg 2x существует.
Мы воспользовались попутно неабсолютным тождеством tg 2x ctg 2x = 1, которое не приводит к приобретению посторонних корней, так как tg 2x и ctg 2x остались в системе.
Преобразуем уравнение следующим образом:
2(tg 3x − tg x) + tg 3x − tg 2x = 0,
т. е.
![]()
Теперь систему можно переписать так:
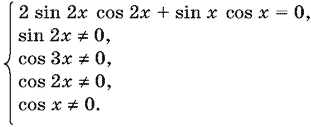
Так как sin 2x ≠ 0, то на него можно сократить. Получим уравнение
cos 2x = −¼,
откуда x = ±arccos(−¼) + kπ. Поскольку при этих x все ограничения выполняются, найденные значения x являются решениями данного уравнения.
Ответ. ±arccos(−¼) + kπ.
13.15. Данное уравнение равносильно системе

Пусть sin x² + cos x² = y. Возведем это соотношение в квадрат: 1 + 2 sin x² cos x² = y², откуда
sin x² cos x² = y² − 1/2.
После подстановки и простых преобразований уравнение примет вид
y² − 2y − 3 = 0,
откуда y1 = −1, y2 = 3. Второй корень посторонний, так как sin x² + cos х² всегда меньше двух.
Если sin x² + cos x² = −1, то
cos (х² − π/4) = −1/√2 и x² = 2nπ ± 3π/4 + π/4.
Взяв знак плюс, получим x² = π(2n + 1). Этот корень посторонний, так как sin x² ≠ 0.
Для знака минус получим, что x² = −π/2 + 2nπ. Это тоже посторонний корень, так как cos x² ≠ 0.
Ответ. Нет решений.
13.16. Данное уравнение равносильно системе

Уравнение можно привести к однородному, домножив 6 sin x на sin² x + cos² x:
3 sin³ x − cos³ x − 2 sin x cos² x = 0.
Обозначим tg x через y, получим
3y³ − 2y − 1 = 0, или (y − 1)(3y² + 3y + 1) = 0,
где квадратный трехчлен не имеет действительных корней.
Остается y = 1, т. е. tg x = 1, x = π/4 + nπ. Однако cos 2x при x = π/4 + nπ обращается в нуль.
Ответ. Нет решений.
13.17. С помощью формул универсальной подстановки придем к уравнению относительно y = tg x/2:
y(2y³ − 7у² − 2y + 1) = 0.
В результате такой замены могли быть потеряны корни, так как tg x/2 теряет смысл при x = π(2k + 1), в то время как sin x, cos x и tg x при этих значениях x имеют смысл. Проверкой убеждаемся, что эти значения неизвестного не являются корнями исходного уравнения.
Один корень полученного алгебраического уравнения очевиден: y = 0. Второй мы найдем на основании теоремы о рациональных корнях многочлена, испытав y = ±1; ±½. Убеждаемся, что y = −½ — второй корень уравнения. Разделив многочлен 2y³ − 7у² − 2y + 1 на 2y + 1, получим уравнение
y² − 4y + 1 = 0,
которое даст еще два корня: y = 2 + √3, y = 2 − √3.
Если tg x/2 = 2 + √3, то
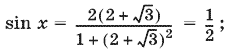
то же самое мы получим и при tg x/2 = 2 − √3.
Так как и обратно из sin x = ½ следует, что

то совокупность уравнений tg x/2 = 2 + √3 равносильна уравнению sin x = ½. Получаем x = kπ + (−1)kπ/6.
Ответ. 2πk; kπ + (−1)k π/6; 2πk − 2 arctg ½.
13.18. Понижением степени данное уравнение приводится к виду
2 cos x = 1 + cos 3x/2.
С помощью формул для косинуса двойного и тройного углов приходим к уравнению относительно y = cos x/2:
4y³ − y² − 3y + 3 = 0.
Левую часть легко разложить на множители:
4у²(y − 1) − 3(y − 1) = 0, (y − 1)(4у² − 3) = 0.
Если cos x/2 = 1, то x1, = 4πn. Если 4 cos² x/2 = 3, то cos x = ½ и x2 = 2πn ± π/3.
Ответ. 4πn; 2πn ± π/3.
13.19. Преобразуем выражение, стоящее в квадратных скобках:
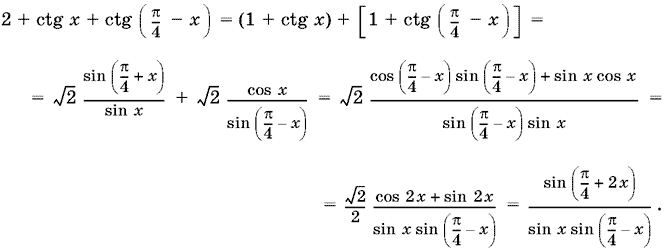
Теперь придем к виду, удобному для логарифмирования, правую часть уравнения:
2√2(1 + sin 2x + cos 2x) = 4√2 cos x(sin x + cos x) = 8 cos x sin (π/4 + x). В итоге получаем уравнение
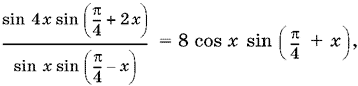
которое равносильно системе
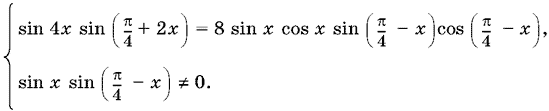
Условие sin x sin (π/4 − x) ≠ 0 подсказывает, что удобнее в левой части уравнения заменить sin 4x на его разложение, стоящее справа, чем наоборот. Сокращая после этого обе части уравнения на 8 sin x sin (π/4 − x) ≠ 0, получим уравнение
cos x cos (π/4 − x)[sin (π/4 + 2x) − 1] = 0.
Среди корней уравнений cos x = 0 и cos (π/4 − x) = 0 не может быть таких, при которых sin x sin (π/4 − x) = 0. Остается проверить корни уравнения sin (π/4 + 2x) = 1. Преобразуем вначале условие, которому они должны удовлетворять: sin x sin (π/4 − x) ≠ 0, или cos (π/4 − 2x) − cos π/4 ≠ 0, т. е. cos (π/4 − 2x) ≠ 1/√2, или sin (π/4 + 2x) ≠ 1/√2. Теперь ясно, что в уравнение sin (π/4 + 2x) = 1 не попали посторонние корни.
Ответ. π/2 + nπ; −π/4 + nπ; π/8 + nπ.
13.20. Перепишем данное уравнение в виде
![]()
т. е.
![]()
После возведения в квадрат (при этом могут появиться посторонние корни, для которых cos x > 0) получим квадратное уравнение относительно y = cos x:
y² − 4у − 4 = 0, т. е. y1,2 = 2 ± 2 √2.
Положительный корень заведомо посторонний. Остается
cos x = 2 − 2 √2.
Ответ. x = π(2n + 1) ± arccos |2( √2 − 1)|.
13.21. Так как sin 4x = 4 sin x cos x(2 cos² x − 1), то данное уравнение можно переписать в виде
sin x [4 cos x (2cos² x − 1) − m/cos x] = 0.
Если sin x = 0, то x = kπ. Это — корни данного уравнения, поскольку cos kπ ≠ 0.
Если выражение в квадратных скобках равно нулю, то приходим к биквадратному уравнению
8 cos4 x − 4 cos² x − m = 0,
среди корней которого не должно быть cos x = 0.
Решая это биквадратное уравнение, получим
![]()
Так как m > 0, то перед корнем берем знак плюс. (Очевидно, что при этом cos x ≠ 0). Воспользуемся формулой
![]()
и преобразуем уравнение к виду
![]()
Правая часть этого уравнения положительна. Поэтому, чтобы уравнение имело решение, достаточно
![]()
откуда m ≤ 4.
Ответ. При m > 0 уравнение имеет решение x = nπ; при 0 < m ≤ 4:
![]()
13.22. Раскроем скобки и применим формулу преобразования произведения синусов в разность косинусов:
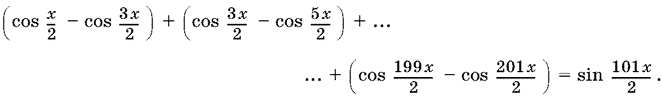
Приведя подобные члены, получим
![]()
откуда
![]()
и
![]()
Ответ.
![]()
13.23. Так как
sin kх sin k²x = 1 {cos [(k − 1)kx] − cos [k(k + 1)x]}, то уравнение можно переписать в виде
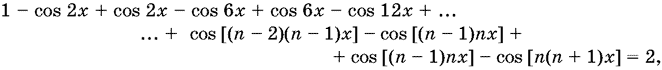
откуда

Ответ.
![]()
где k = 0, +1, +2, ..., а натуральное n фиксировано.
13.24. Перенесем единицу в левую часть и запишем уравнение в виде
2 cos x − cos 2x − cos² 2x = 0,
или
2 cos x − cos 2x (1 + cos 2x) = 0.
Выражение в скобках равно 2 cos² x. Поэтому
cos x (1 − cos x cos 2x) = 0.
Если cos x = 0, то x = π/2 + nπ.
Если cos x cos 2x = 1, то

Второе уравнение первой системы преобразуется к виду 2 cos² x − 1, т. е. cos² x = 1. Следовательно, cos x = 1 и x = 2nπ.
Для второй системы аналогично получим cos² x = 0, что несовместно с первым уравнением cos x = −1.
Ответ. π/2 + nπ; 2nπ.
13.25. Данное уравнение эквивалентно совокупности двух систем
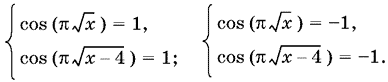
Первая система может быть переписана так:
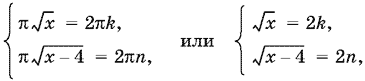
откуда

(Для k и n берутся только неотрицательные значения.) Приравнивая различные выражения для x, получим k² = n² + 1, откуда (k − n)(k + n) = 1. Так как k и n — целые и неотрицательные, то
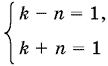
и, следовательно k = 1, n = 0.
Теперь x определяется однозначно: x = 4.
Решаем вторую систему:
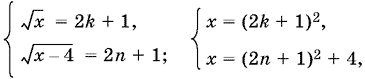
где k, n = 0, 1, 2, ... .
Приравнивая правые части последней системы, получим
(2k + 1)² − (2n + 1)² = 4, или (k − n)(k + n + 1) = 1.
Так как n и k — целые и неотрицательные числа, то последнее уравнение равносильно системе

которая не имеет целых решений.
Ответ. 4.
13.26. Данное уравнение можно переписать в виде
sin³ x + cos³ x = sin² x + cos² x,
откуда
sin² x (1 − sin x) + cos² x (1 − cos x) = 0.
Сумма двух неотрицательных слагаемых равна нулю тогда и только тогда, когда оба слагаемых равны нулю:

Если в первом уравнении sin x = 0, то cos x ≠ 0. Получаем систему решения которой: x = 2kπ.

Если в первом уравнении 1 − sin x = 0, т. е. sin x = 1, то cos x ≠ 1. Приходим к системе

решения которой: x = π(4k + 1)/2.
Ответ. 2kπ; π(4k + 1)/2.
13.27. Способ 1. Дополним левую часть данного уравнения до полного квадрата. Для этого придется ввести еще одно слагаемое: cos x cos 3x, знак которого зависит от знака cos x, так как из данного уравнения следует, что cos 3x ≥ 0.
Рассмотрим три случая.
1. Если cos x > 0, то перепишем данное уравнение в виде
cos² 3x + ¼ cos² x − cos x cos 3x = cos 3x cos4 x − cos 3x cos x,
или
(cos 3x − ½ cos x)² + cos x cos 3x (1 − cos³ x) = 0.
В левой части стоит сумма неотрицательных выражений, следовательно,
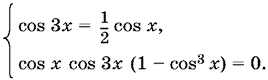
По предположению cos x > 0. Из первого уравнения последней системы следует, что тогда cos 3x > 0. Заметим, что
1 − cos³ x = (1 − cos x)(1 + cos x + cos² x),
причем всегда 1 + cos x + cos² x > 0. В итоге приходим к системе
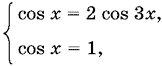
которая несовместна, так как при cos x = 1 мы получим cos 3x = 1, а не ½.
2. Если cos x = 0, то cos 3x = 4 cos³ x − 3 cos x = 0, и данное уравнение удовлетворяется. Получаем совокупность корней: x = π/2 + nπ.
3. Если cos x < 0, то преобразуем уравнение к виду
(cos 3x + ½ cos x)² + cos 3x cos x (−1 − cos³ x) = 0,
в котором снова оба слагаемых неотрицательны. Аналогично случаю 1, это приводит нас к несовместной системе (закончить исследование самостоятельно).
Способ 2. Уравнение можно рассматривать как квадратное относительно cos 3x:
cos² 3x − cos 3x cos4 x + ¼ cos² x = 0.
Следовательно,
![]()
Условие cos8 x − cos² x = cos² x (cos6 x − 1) ≥ 0 является следствием данного уравнения. Если cos² x = 0, то x = π/2 + πk; эти значения x удовлетворяют первоначальному уравнению. Если же cos² x = 1, то исходное уравнение примет вид
cos² 3x − cos 3x + ¼ = 0, т. е. cos 3x = ½.
Из первого условия cos² x = 1 находим x = πk. Так как cos 3πk ≠ 2 , то в этом случае решений мы не получаем.
На этом примере хорошо видно, что отказ от равносильных преобразований может позволить решить задачу проще и короче.
Ответ. π/2 + nπ.
13.28. Данное уравнение равносильно системе
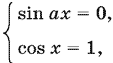
решая которую найдем ах = kπ и x = 2nπ. Приравнивая значения неизвестного, найденные из каждого уравнения, получим
kπ/a = 2nπ, т. е. k/a = 2n.
Это в том случае, если а ≠ 0. Но если а = 0, данное уравнение примет вид cos x = 1 и, следовательно, имеет бесконечное множество корней.
Итак, k = 2nа.
Если а = p/q — рациональное число, то k = 2np/q. Это значит, что при всех n, кратных q, мы будем получать корень данного уравнения x = 2nπ, т. е. уравнение имеет бесконечное множество корней.
Пусть теперь а — иррациональное число. Тогда при всех n, кроме n = 0, k не будет целым, а уравнение будет иметь единственное решение x = 0.
Ответ. а — иррациональное.
13.29. Так как второе уравнение легко приводится к виду
sin (2x − y) = 0,
то y = 2x + πk. После подстановки этих значений y в первое уравнение получим
4 tg Зх = 3 tg 4x, или 4 (tg 4x − tg Зх) = tg 4x.
Используя простые преобразования, приходим к равносильным уравнениям:

Выражение, стоящее в скобках, может обратиться в нуль лишь при условии, что cos x, cos 2x, cos Зх одновременно равны по абсолютной величине единице. Это означает, что непременно |cos x| = 1, т. е. корнями выражения, заключенного в скобки, могут быть лишь числа x = πn, являющиеся также и корнями множителя sin x. (Обратите внимание на то обстоятельство, что здесь нельзя написать x = πk, поскольку буква k уже занята в записи решения второго уравнения.)
Таким образом, все решения данной системы содержатся в системе чисел x = πn, y = π(2n + k), которую можно переписать так: x = πn, y = πk. Непосредственной подстановкой в исходную систему убеждаемся, что каждая пара из системы этих значений x и y является решением.
Ответ. x = πk, y = πn.
13.30. Преобразовав левую часть второго уравнения в разность косинусов, получим
cos (2y + x) = О, откуда 2y = 2 − x + kn.
Приведем теперь первое уравнение системы к виду, удобному для логарифмирования:
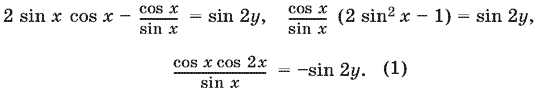
При подстановке в правую часть значения 2y, полученного ранее, придется рассматривать случаи k = 2p и k = 2p + 1.
Если k = 2p, то
2y = π/2 − x + 2pπ
и sin 2y = cos x. Уравнение (1) преобразуется к виду
![]()
Если же k = 2p + 1, то
2y = π/2 − x + π + 2pπ = 3π/2 − x + 2pπ
и sin 2y = −cos x. Уравнение (1) теперь примет вид
![]()
Поскольку значения x, при которых cos x = 0, удовлетворяют как уравнению (2), так и уравнению (3), то значениям x = (2n + 1)π/2 соответствуют все целые значения k. Поэтому
2y = π/2 − x + πk = π − πn + πk = π(k − n + 1).
Так как k − n + 1 принимает все целые значения для любого фиксированного k, то можно обозначить k − n + 1 = p. Получаем систему решений

Остается приравнять нулю, выражения, стоящие в скобках в уравнениях (2) и (3).
Для уравнения (2) имеем
sin x + cos 2x = 0, cos 2x = cos (x + π/2),
откуда x2 = (4n + 1)π/2, x3 = (4n − 1)π/6. Получаем еще две системы решений (здесь k = 2p)
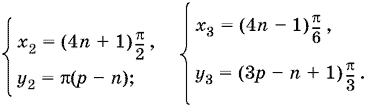
Для уравнения (3)
cos 2x − sin x = 0, cos 2x = cos (π/2 − x),
откуда x4 = (4n − 1)π/2, x5 = (4n + 1)π/6. В этом случае k = 2p + 1, и мы находим еще две системы решений
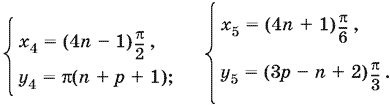
Нетрудно заметить, что вторая и четвертая системы решений содержатся в первой.
Проверка не нужна. (Докажите.)
Ответ.
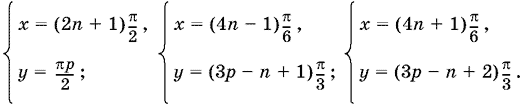
13.31. Перепишем систему в виде
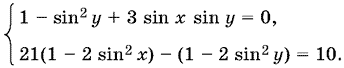
Введем обозначения: sin x = u, sin y = v. Получим систему
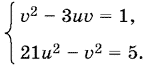
Воспользуемся заменой v = ut:
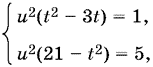
откуда
5(t² − 3t) = 21 − t²,
т. е.
2t² − 5t − 7 = 0, t1 = 7/2, t2 = −1.
Если t = 7/2, то из первого уравнения последней системы мы получим
u² = 4/7; u ±2/√7; v = ut = ±2/√7 7/2 = ±√7,
что невозможно, так как v = sin y.
Если же t = −1, то u² = ¼, u = ±½.
Приходим к совокупности двух систем
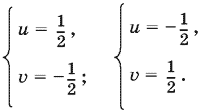
Ответ.
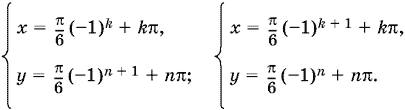
13.32. Второе уравнение можно преобразовать так:
sin y + sin (2x − y) = sin y,
т. е. sin (2x − y) = 0, откуда y = 2x + nπ. Подставим в первое уравнение системы
4 tg 3x = 3 tg 4x.
При условии что cos 3x ≠ 0 и cos 4x ≠ 0, это уравнение равносильно такому:
4 sin 3x cos 4x − 3 sin 4x cos 3x = 0,
или
sin 3x cos 4x − 3 (sin 4x cos 3x − sin 3x cos 4x) = 0,
sin 3x cos 4x − 3 sin x = 0.
Так как sin 3x cos 4x = ½(sin 7х − sin x), то придем к уравнению
7 sin x = sin 7x.
По индукции можно доказать, что
sin пх ≤ n|sin x|,
причем равенство достигается лишь при x = kπ. Следовательно, уравнение 7 sin x = sin 7х имеет решения x = kπ.
При этом cos 3x ≠ 0 и cos 4x ≠ 0.
Подставляя в выражение для y, получим y = nπ.
Ответ. x =kπ, y = kπ.
13.33. Возведем каждое уравнение в квадрат и сложим:
2 = sin² y + 5 cos² y,
откуда cos² y = ¼, т. е. cos y = ±½.
Учитывая второе уравнение исходной системы, приходим к совокупности двух систем
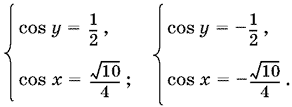
Возводя при решении оба уравнения в квадрат, мы могли приобрести посторонние решения. Отсеять их можно просто: достаточно выбрать sin x и sin y так, чтобы они имели одинаковый знак (для cos x и cos y мы это уже обеспечили). Оба этих требования означают, что x и y должны лежать в одной четверти.
Решая первую систему, получим
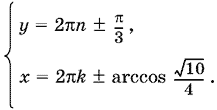
Значения x и y будут лежать в одной четверти, если мы одновременно возьмем только верхние или только нижние знаки.
Аналогично поступаем со второй системой.
Ответ.
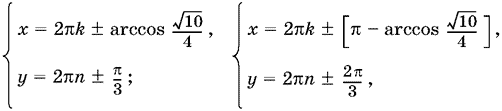
где одновременно берут либо только верхние, либо только нижние знаки.
13.34. Так как sin πx²/2 = 1, то
πx²/2 = π/2 + 2πn,
откуда x² = 4n + 1 и
![]()
Подставив во второе уравнение, найдем
![]()
Чтобы это равенство выполнялось, необходимо
![]()
откуда n ≤ 2.
Ответ.
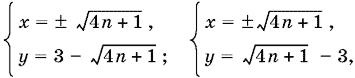
где n = 0, 1, 2. Всего 12 решений (10 не совпадающих).
13.35. Разделив второе уравнение на первое, получим tg y = 2 tg x. Так как x + y = π − z, то tg z = −tg (π − z) = −tg (x + y).
По формуле тангенса суммы получаем
![]()
Применение неабсолютного тождества не приводит к потере решений, так как tg x и tg y входят в данную систему.
Подставляем в первое уравнение
![]()
откуда tg² x = 1, x = kπ ± π/4. Найти y и z теперь не составляет труда.
Производя вычисления отдельно для x = kπ + /4 и для x = kπ − /4, после проверки получим решение системы.
Ответ.

13.36. Так как в уравнения системы входят одновременно tg x и ctg x, tg y и ctg y, то неизвестные не могут принимать значения kπ/2. С учетом этого данную систему можно записать сначала так:
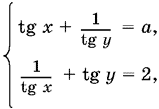
а затем так:

откуда а tg y = 2 tg x.
Если а = 0, то tg x = 0, а ctg x не существует. Поэтому а ≠ 0 и tg y = 2/a tg x. Подставляем в первое уравнение системы
tg x + a/2 tg x = a, т. е. 2 tg² x − 2a tg x + a = 0.
Решаем последнее уравнение:
![]()
и находим tg y:
![]()
Дискриминант стоящего слева квадратного трехчлена равен а² − 2a. Он неотрицателен, если а ≤ 0 или а ≥ 2. Значение а = 0 нужно исключить.
При остальных а ни tg x, ни tg y не обращаются в нуль и существуют. Остается сделать проверку.
Ответ. Если а < 0 или а ≥ 2, то
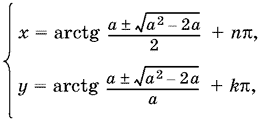
где одновременно берутся либо верхние, либо нижние знаки.
13.37. Перенесем sin y и cos y в правую часть:
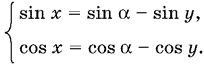
Возведем каждое уравнение в квадрат и сложим:
1 = 2 − 2(sin α sin y + cos α cos y),
т. е. cos (y − α) = ½. Таким образом, y − α = 2nπ ± π/3. Аналогично найдем x − α = 2kπ ± π/3.
Система еще не решена, так как при возведении в квадрат могли быть приобретены посторонние корни. Чтобы сделать проверку, подставим x = α + 2kπ ± π/3 и y = α + 2nπ ± π/3 в данную систему:

Обратим внимание на то, что в этой записи не исключается возможность выбора произвольных комбинаций знаков плюс и минус для x и y.
Если в выражениях для x и y взять одинаковые знаки, например плюс, то получим систему
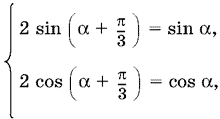
откуда следует
tg (α + π/3) = tg α или ctg (α + π/3) = ctg α,
что неверно при всех α.
Если взять разные знаки, то
sin (α + π/3) + sin (α − π/3) = 2 sin α cos π/3 = sin α,
cos (α + π/3) + cos (α − π/3) = 2 cos α cos π/3 = cos α,
т. е. каждое уравнение системы превращается в тождество.
Ответ.
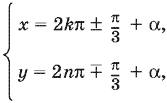
где берутся или только верхние, или только нижние знаки.
Замечание. Найдя y = α + 2nπ ± π/3, можно было искать x с помощью подстановки. Однако это не избавило бы нас от необходимости делать проверку, так как в процессе решения уравнения возводились в квадрат.
13.38. Первое уравнение перепишем в виде
sin (x − y) − cos (x + y) = 2a.
Из второго найдем
cos (x + y) = cos [2 arcsin (a + ½)] = 1 − 2 sin² [arcsin (a + ½)] = 1 − 2(a + ½)² = ½ − 2a² − 2a.
Следовательно,
sin (x − y) = 2a + cos (x + y) = ½ − 2a² = 1 − 4a²/2.
Прежде чем решать систему
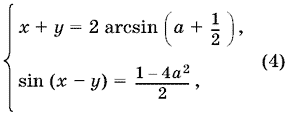
выясним, при каких а она имеет решение.
Первоначальная система накладывает на параметр а такие ограничения: |а| ≤ 1, | а + ½| ≤ 1, где первое — следствие того, что в левой части первого уравнения стоит произведение синуса и косинуса, а второе — следствие определения арксинуса.
Поскольку при преобразованиях исходной системы равносильность не нарушалась, то нет необходимости учитывать первоначальные ограничения, так как они будут содержаться в ограничениях системы (4):
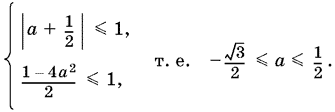
Итак, если параметр а лежит на интервале −√3/2 ≤ а ≤ ½, то систему (4) можно переписать в виде

Решая эту систему, найдем x и y. Остается сделать проверку.
Ответ. При −√3/2 ≤ а ≤ ½

13.39. Обозначим tg² x = u, tg² y = v. Тогда в левой части уравнения получим u² + v² + 2/uv. Это выражение не может стать меньше, чем 2uv + 2/uv, так как u² + v² ≥ 2uv. Выражение 2uv + 2/uv тоже легко оценить:
2[uv + 1/uv] ≥ 4,
причем равенство в первом и во втором случаях достигается лишь при u = v = 1.
Таким образом, сумма, стоящая в левой части равенства, не может стать меньше 4, в то время как правая часть этого равенства не может превзойти 4. Остается единственная возможность: обе части равенства одновременно равны 4. Получаем систему

Второму уравнению удовлетворяют значения x = ±π/4 + kπ, y = ±π/4 + nπ, где знаки берутся в произвольных сочетаниях. Однако первое уравнение будет удовлетворяться только в том случае, когда в выражениях для x и y взяты одинаковые знаки.
Ответ.
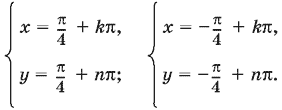
13.40. Способ 1. Умножив sin² x на sin² 3x + cos² 3x = 1 и сгруппировав члены, содержащие sin² 3x, получим
sin² x cos² 3x + sin² 3x(sin² x − sin x + ¼) = 0,
или
sin² x cos² 3x + sin² 3x(sin x − ½)² = 0.
Последнее уравнение эквивалентно системе

Корни первого уравнения найти нетрудно:
x1 — nπ, x2 = π/6 + nπ/3.
Подставляя x1 во второе уравнение, убеждаемся, что оно удовлетворяется при этих значениях неизвестного. Подставляя во второе уравнение x2, получим
sin (π/2 + nπ) [sin (π/6 + nπ/3) − ½] = 0.
Так как первый сомножитель никогда не обращается в нуль, то последнее равенство можно записать так:
sin (π/6 + nπ/3) = sin π/6.
Воспользовавшись условием равенства синусов (если sin α = sin β, то либо α − β = 2kπ, либо α + β = (2k + 1)π), получим
π/3 + nπ/3 = (2k + 1)π, откуда n = 6k + 2,
и
nπ/3 = 2kπ, откуда n = 6k.
Таким образом,
x1 = nπ, x2 = π/6 + 2kπ, x3 = 5π/6 + 2kπ.
Способ 2. Перепишем уравнение в виде
4 sin² x − 4 sin x sin² 3x + sin² 3x = 0,
т. е.
(2 sin x − sin² 3x)² + (sin² 3x − sin4 3x) = 0.
Так как оба слагаемых неотрицательны, то
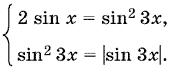
Из второго уравнения получим: либо sin 3x = 0 и x = nπ/3, либо |sin 3x| = 1 и x = π/6 + nπ/3. Остается отобрать из этих решений те, которые удовлетворяют первому уравнению, что делается так же, как и в первом способе решения.
Способ 3. Рассмотрим данное уравнение как квадратное относительно sin x. Тогда
![]()
Чтобы уравнение имело действительные решения, необходимо и достаточно потребовать неотрицательности дискриминанта
sin² 3x (sin² 3x − 1) ≥ 0.
Выражение в скобках не может стать положительным. Следовательно, остается лишь две возможности: либо sin² 3x = 0, либо sin² 3x = 1. Если sin² 3x = 0, то, подставляя в первоначальное уравнение, получим sin² x = 0, т. е. x = πk. Если sin² 3x = 1, то придем к квадратному уравнению
sin² x − sin x + ¼ = 0, откуда sin x = ½.
Ответ. nπ; π/6 + 2kπ; 5π/6 + 2kπ.
13.41. Способ 1. Преобразовав данное уравнение к функциям от x + y/2 и x − y/2 и дополнив полученное таким образом выражение до полного квадрата, придем к уравнению вида
(2 cos x + y/2 − cos x − y/2)² + sin² x − y/2 = 0.
Это уравнение эквивалентно системе
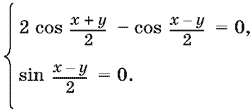
Решая второе уравнение системы, найдем
x − y/2 = nπ,
откуда x − y = 2nπ, а x = y + 2nπ.
Подставляя найденное выражение для x в первое уравнение, получим
2 cos (y + nπ) − cos nπ = 0.
Число n может быть либо четным, либо нечетным. Если n = 2k, то уравнение примет вид 2 cos y − 1 = 0, откуда cos y = ½.
При n = 2k + 1 получим −2 cos y + 1 = 0, откуда снова cos y = ½. Таким образом,
y = 2πm ± π/3, а x = y + 2nπ = 2π(n + m) ± π/3.
В этом случае n + m можно рассматривать как новое целочисленное переменное и записать ответ следующим образом:

Способ 2. Преобразовав уравнение к виду A cos y + В sin y = 3/2 − cos x, где A = 1 − cos x, В = sin x (причем A и В не равны нулю одновременно), оценим его левую часть
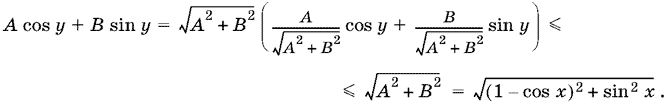
Чтобы данное уравнение имело решение, необходимо, чтобы
(1 − cos x)² + sin² x ≥ (3/2 − cos x)²
или
cos² x − cos x + ¼ ≤ 0, т. е. (cos x − ½) ≤ 0.
Так как квадрат некоторого выражения не может быть отрицательным, то cos x = ½, откуда
x = 2nπ ± π/3.
Чтобы найти y, можно подставить найденные значения x в исходное уравнение. Однако достаточно заметить, что исходное уравнение симметрично относительно x и y. Следовательно, для второго неизвестного мы тоже получим
y = 2mπ ± π/3.
Остается установить соответствие между найденными значениями x и y, что легко сделать проверкой, так как здесь нужно рассмотреть всего четыре различные возможности. Убеждаемся, что из четырех возможностей уравнению удовлетворяют только две, когда для x и y выбраны одинаковые знаки.
Ответ. x = 2nπ ± π/3, y = 2mπ ± π/3; где берутся либо только верхние, либо только нижние знаки.
13.42. Способ 1. Задача сводится к отысканию таких а и b, при которых равенство
tg x + tg (а − x) + tg x tg (а − x) = b является неабсолютным тождеством. Обозначив tg x = z и tg а = с (в предположении, что а ≠ π/2 (2n + 1)), получим
![]()
Перенеся все в левую часть и приведя к общему знаменателю, получим
![]()
Это уравнение относительно z является неабсолютным тождеством тогда и только тогда, когда многочлен, стоящий в числителе, обращается в нуль при всех z, кроме, быть может, одного значения z, обращающего в нуль знаменатель левой части, что равносильно тождественному равенству нулю этого многочлена. Так как условием тождественного равенства многочлена нулю является равенство нулю всех его коэффициентов, то получим с = 1, b = 1, т. е. b = 1, а = π/4 + kπ. Случай а = (2n + 1)π/2 приводит к равенству tg x + ctg x = b − 1, которое является неабсолютным тождеством.
Способ 2. Равенство
tg x + tg (а − x) + tg x tg (а − x) = b
должно удовлетворяться тождественно по отношению к x. Положив x = 0, получим, что либо tg а = b, либо tg а не существует, т. е. а = (2n + 1)π/2. Аналогично для x = π/4 получим, что либо tg (а − π/4) = b − 1/2, либо а − π/4 = π/2 + πn, т. е. а = 3π/4 + πn.
Итак, если а ≠ (2n + 1)π/2 и а ≠ 3π/4 + πn, то получаем систему, которой должны удовлетворять а и b:
tg а = b, tg (а − π/4) = b − 1/2.
Заменив во втором уравнении b на tg а, перепишем его в виде
![]()
откуда tg а = 1. Таким образом, b = 1, а = π/4 + nπ. Проверим, будет ли при этих значениях а и b равенство, написанное в начале решения, неабсолютным тождеством. После подстановки получим
tg x + tg (π/4 + nπ − x) + tg x tg (π/4 + nπ − x) = 1
или
![]()
т. е. равенство
![]()
являющееся неабсолютным тождеством.
Остается рассмотреть исключенные значения параметра а. Если а = (2n + 1)π/2, то приходим к равенству tg x + ctg x = b − 1, являющемуся неабсолютным тождеством. Когда а = 3π/4 + πn, то tg а = −1 и, следовательно, b = tg а = −1. При этом исходное равенство принимает вид
tg x + ctg (x − π/4) + tg x ctg (x − π/4) = −1.
Оно является неабсолютным тождеством, так как при π/4 < x < π/2 функции tg x и ctg (x − π/4) положительны, а потому левая часть равенства не может быть равна −1.
Ответ. а = π/4 + nπ, b = 1.
13.43. Оценим левую часть уравнения:
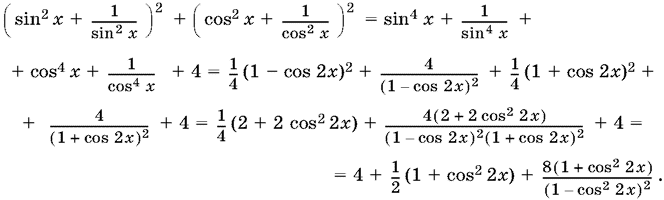
С увеличением cos² 2x это выражение растет. Поэтому оно будет достигать своего минимума, когда cos² 2x = 0. Таким образом, левая часть уравнения не может стать меньше 12,5.
Поскольку правая часть не может превзойти 12,5, то получаем систему
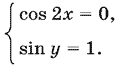
Ответ.

13.44. Представив данное уравнение в виде
sin 2x − sin x cos 2x = 3/2,
оценим левую часть. Чтобы оценить выражение
A sin 2x + В cos 2x,
его нормируют, т. е. представляют в виде
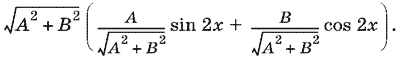
Выражение, стоящее в скобках, можно записать как sin (2x + α), т. е. оно не превосходит по абсолютной величине единицу. В нашем случае A = 1, В = −sin x. Поэтому
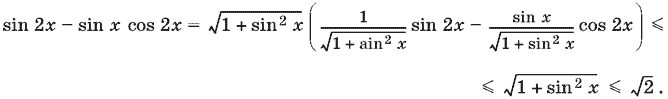
Так как левая часть рассматриваемого уравнения не превосходит √2, а правая часть равна 2, что больше √2, то данное уравнение не имеет корней.
Ответ. Нет решений.
13.45. Раскроем скобки и произведем перегруппировку членов:
(sin x cos x/4 + cos x sin x/4) − (2 sin² x + 2 cos² x) + cos x = 0,
т. е.
sin 5x/4 + cos x = 2.
Так как sin 5x/4 ≤ 1 и cos x ≤ 1, то последнее уравнение равносильно системе
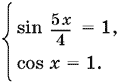
Решения второго уравнения x = 2πk подставим в первое уравнение. Выражение sin 5πx/2 перепишем в виде sin (2πk + 5πx/2) = sin πk/2, откуда следует, что sin 5x/4 = 1 лишь при k = 4n + 1.
Ответ. x = 2π(4n + 1).
13.46. Введем новое неизвестное

Получим квадратное уравнение относительно y:
![]()
корни которого
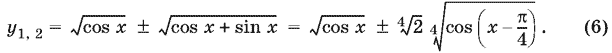
Обозначим
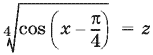
и подставим в (6) вместо y его выражение (5) через x. Получим следствие исходного уравнения
![]()
т. е.
±z² + 4z − 5 = 0. (7)
Решая каждое из квадратных уравнений (7), найдем два действительных корня: z1 = −5, z2 = 1. Из них подходит только 2 = 1. Следовательно,
cos (x − π/4) = 1, откуда x = π/4 + 2nπ.
Остается сделать проверку, которая осуществляется непосредственной подстановкой в исходное уравнение.
Ответ. x = π/4 + 2nπ.
13.47. Система уравнений может быть переписана так:

Если cos x = 0, то x = (2k + 1)π/2 и, следовательно, cos 7x = 0. Поэтому первое уравнение равносильно уравнению cos 7 x = 0, т. е.
2 cos² 7x/2 = 1 и cos² 7x/2 = ½.
Возведя второе уравнение системы в квадрат, получим теперь, что одновременно и cos² x/2 = ½. Таким образом, исходная система уравнений равносильна совокупности двух систем

в которых множество решений вторых уравнений входит в множество решений первых. (Докажите.) Это означает, что система сводится к совокупности двух вторых уравнений
cos x/2 = ±1/√2, т. е. cos² x/2 = ½,
откуда cos x = 0 и x = (2k + 1)π/2. Из найденной серии чисел отбираем те, которые удовлетворяют ограничению |x| < 5.
Ответ. x = ±π/2, ±3π/2.
13.48. Преобразуем левую часть уравнения, пользуясь тем, что tg x = sin x/cos x, tg² x = 1/cos² x − 1, а cos x ≠ 0:
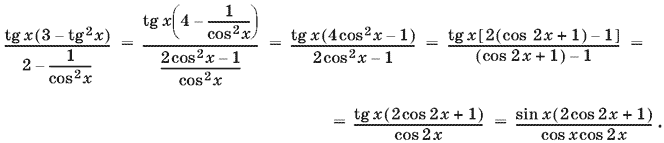
Для правой части уравнения получим

При cos x ≠ 0 и дополнительном ограничении cos 2x ≠ 0 приведем исходное уравнение к виду
2 sin x cos 2x + sin x = 2 + cos 6x/5.
Произведение 2 sin x cos 2x преобразуем в разность синусов. Тогда в левой части останется только sin 3x (так как 2sin x cos 2x = sin 3x − sin x) и уравнение примет вид
sin 3x = cos 6x/5 + 2.
Такое возможно лишь при условии, что одновременно
cos 6x/5 = −1, а sin 3x = 1.
Поэтому данное в условии уравнение равносильно системе:
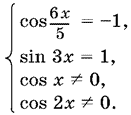
Не следует решать каждое из уравнений и отдельно записывать для них общие ограничения. Это не приведет к результату. Лучше начать с первого уравнения — его корни имеют простую запись, а затем отсеивать из решений первого уравнения те, что не удовлетворяют остальным требованиям. Итак, из уравнения cos 6x/5 = −1 найдем, что
6x/5 = π(2k + 1), т. е. x = 5(2k + 1)π/6.
Проверим, чему равняется при найденных x значение sin 3x. Поскольку
3x = 5(2k + 1)π/2 = 5πk + 5π/2,
то найти sin 3x мы сможем, рассмотрев две возможности: k = 2n, k = 2n + 1.
При k = 2n, т. е. k — четном
3x = 10πn + 5π/2 = 10πn + 2π + π/2.
Мы выделили период и поэтому sin 3x при k = 2n равняется sin π/2 = 1, т. е. второе уравнение системы удовлетворяется. Если же k = 2n + 1, т. е. k — нечетное, то
3x = 5π(2n + 1) + 5π/2 = 10πn + 5π + 2π + π/2 = 10πn + 4π + π + π/2,
т. е. sin 3x = −1. На этот раз второе уравнение системы не удовлетворяется.
Обоим уравнениям удовлетворяют значения x = 5(4n + 1)π/6. (Мы просто подставили k = 2n в найденное выше выражение для x.)
Перейдем к ограничению cos x ≠ 0. Преобразуем выражение для x:
x = 20πn/6 + 5π/6 = 10πn/3 + 5π/6.
Чтобы при разных n вычислить cos x, нужно рассмотреть случаи n = 3m, n = 3m + 1, n = 3m − 1. (Обратите внимание, что вместо n = 3m − 1 можно рассматривать n = 3m + 2, но n = 3m − 1 удобнее.)
Для n = 3m получим
x = 10πm + 5π/6, cos x = cos 5π/6 ≠ 0;
при n = 3m + 1:
x = 10π3m + 1/3 + 5π/6 = 10πm + 10π/3 + 5π/6 = 10πm + 25π/6 = 10π0 + 4π + π/6,
т. е. cos x = cos π/6 ≠ 0,
при n = 3m − 1:
x = 10π3m − 1/3 + 5π/6 = 10πm − 10π/3 + 5π/6 = 10πm − 15π/6 = 10πm − 2π − π/2,
т. е. cos x = cos (−π/2) = 0.
Итак, значение n = 3m − 1 не подходит, а при остальных n ограничение cos x ≠ 0 удовлетворяется.
Остаются два варианта:
x = 5(12m + 1)π/6, x = 5(12m + 5)π/6, m = 0, ±1, ±2.
Непосредственной подстановкой убеждаемся, что cos 2 x ≠ 0 для каждого из найденных значений.
Ответ. 5(12m + 1)π/6; 5(12m + 5)π/6.
13.49. Обе части уравнения существуют, если cos x ≠ 0, sin 2x ≠ 0, cos 2x ≠ 0.
Все эти ограничения равносильны условию sin 4x ≠ 0, поскольку
sin 4x = 2 sin 2x cos 2x = 4 sin x cos x cos 2x.
Если sin 4x ≠ 0, то все последующие преобразования правомерны. Преобразуем левую часть, воспользовавшись соотношениями:
tg² x + 1 = 1/cos² x, cos 3x + cos x = 2 cos 2x cos x.
Тогда
![]()
Так как cos 2x ≠ 0, cos x ≠ 0, то
4 cos² x − 1 = cos 3x/sin x.
Поскольку 2 cos² x = 1 + cos 2x и sin x ≠ 0, получим
2 cos 2x sin x + sin x = cos 3x,
или
sin 3x − sin x + sin x = cos 3x,
т. е. tg 3x = 1, откуда 3x = π/4 + πk = π/4(4k + 1), k = 0, ±1, ±2, или x = π/12(4k + 1).
Теперь нужно позаботиться о соблюдении ограничения sin 4x ≠ 0, т. е. 4x ≠ πn, x ≠ πn/4.
Равенство
π/12(4k + 1) = πn/4, или π/3(4k + 1) = πn, (8)
может иметь место, когда 4k + 1 делится на 3. Поэтому рассмотрим три случая: k = 3m, k = 3m + 1, k = 3m − 1. Тогда для 4k + 1 получим
4(3m) + 1 = 12m + 1,
4(3m + 1) + 1 = 12m + 5,
4(3m − 1) + 1 = 12m − 3 = 3(4m − 1).
Последний из вариантов должен быть исключен, так как именно в этом случае равенство (8) имеет место.
Ответ. π/12(12m + 1); π/12(12m + 5).
13.50. Представим уравнение в виде
2(tg x + ctg 2x) + (tg x/2 + ctg 2x) + (ctg 2x − ctg 3x) = 0.
Преобразуем

(Сокращение на cos x возможно, так как ограничение cos x ≠ 0 остается благодаря наличию множителя cos x в знаменателе sin 2x.)
Аналогично
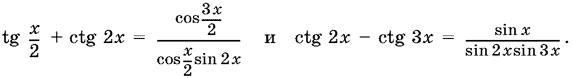
(Во второй дроби sin x − общий множитель числителя и знаменателя. Однако сокращать на него не следует, хотя это и возможно).
Таким образом, уравнение примет вид:
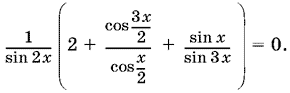
После сложения дробей в скобках получим числитель, который, шаг за шагом, преобразуем:

Итак, данное уравнение преобразовано к равносильному ему:

Нужно найти корни числителя, при которых знаменатель не обращается в нуль. Сомножитель cos x ≠ 0, так как в знаменателе есть sin 2x = 2 sin x cos x. Второй сомножитель тоже не равен нулю, так как входит множителем и в числитель, и в знаменатель. Остается sin 5x/2 = 0, что имеет место при 5x/2 = πk, т. е. при x = 2πk/5, где k = 0, ±1, ±2.
Отсеим из этого множества чисел значения, при которых знаменатель обращается в нуль. Это будет, когда k делится на 5, т. е. k = 5n.
При остальных k, т. е. при k = 5n ± 1 и k = 5n ± 2 знаменатель в нуль не обращается.
Ответ. 2π(5n ± 1)/5, 2π(5n ± 2)/5.
13.51. Ограничения sin t ≠ 0 и cos t ≠ 0 объединяет условие sin 2t ≠ 0. Учтем, что
sin 3t − sin t = 2 sin t cos 2t, ctg² t + 1 = 1/sin² t.
Тогда уравнение (мы учли, что sin 2t ≠ 0) примет вид

или
![]()
Так как 2 cos² t = 1 + cos 2t, а 2 sin² t = 1 − cos 2t, то после сокращения дроби в левой части уравнения на cos 2t получим
cos t = 1/2 cos 2t − 1,
где cos 2t ≠ 0.
Если cos 2t ≠ ½, то
2 cos 2t cos t − cos t = 1,
или
cos 3t + cos t − cos t = 1,
т. е. cos 3t = 1 и t = 2πk/3 , k = 0, ±1, ±2, ... .
Остается учесть все ограничения:
sin 2t ≠ 0, cos 2t ≠ 0, cos 2t ≠ ½.
Условия sin t ≠ 0, cos t ≠ 0, cos 2t ≠ 0 можно объединить: sin 4t ≠ 0. Из значений неизвестного t = 2πk/3 нужно исключить те, при которых имеет место одно из равенств: sin 4t = 0 или cos 2t = ½. Первое равенство будет иметь место, когда k делится на 3, т. е. k = 3n. Остаются две возможности: k = 3m + 1 и k = 3m − 1. Итак, остались для проверки значения:
t = 2π(3m + 1)/3 и t = 2π(3m − 1)/3.
Среди них не должно быть таких, что cos 2t = 1. Вычислим cos[2π(3m + 1)/3] и cos[2π(3m − 1)/3]
cos[2π(3m + 1)/3] = cos (2πm + 2π/3) = cos 2π/3 = −½,
cos[2π(3m − 1)/3] = cos (2πm − 2π/3) = cos (−2π/3) = −½.
Ответ. 2π(3m ± 1)/3.