Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Последовательности и прогрессии
19.1. Сравним n−й и (n + 1)−й члены последовательности (здесь V — знак сравнения):
![]()
или после упрощений:
![]()
Так как
(n + 1/n)n = (1 + 1/n)n = 1 + n · 1/n + ...,
где многоточиями обозначены некоторые положительные члены, то
(n + 1/n)n > 2 при n > 1.
Следовательно, последовательность убывающая, начиная со второго члена.
19.2. Так как аp, аq, аr и аs — члены арифметической прогрессии, то
aq − aр = d(q − p), ar − aq = d(r − q), as − ar = d(s − r).
Кроме того, aрar = aq², aqas = ar², apas = aqar, что отражает условие, в силу которого aр, aq, ar и as образуют геометрическую прогрессию. Из первой группы формул имеем
![]()
Составим произведение (p − q)(r − s) и воспользуемся второй группой формул:

что и доказывает сформулированное в условии утверждение.
19.3. По условию
a = a1 + d(m − 1) = u1qm − 1, b = a1 + d(n − 1) = u1qn − 1, c = a1 + d(p − 1) = u1qp − 1.
Составим разности:
b − с = d(n − p), с − а = d(p − m), а − b = d(m − n).
Подставим в левую часть равенства, которое нужно доказать:
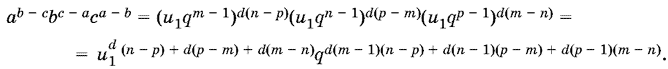
После несложных преобразований получим в обоих показателях нули, что и доказывает равенство произведения единице.
19.4. Перейдем в левой части равенства к общему основанию x и сделаем некоторые упрощения:

В последнем равенстве мы воспользовались тем, что b/a = c/b = q — знаменателю прогрессии, а также тем, что
![]()
19.5. Имеем
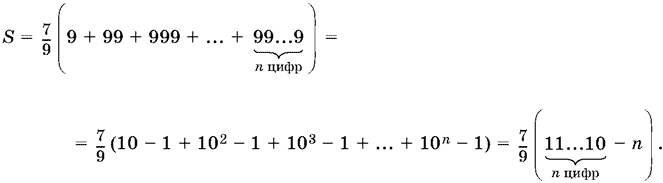
Ответ.
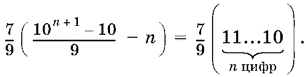
19.6. Преобразуем выражение, стоящее под знаком квадратного корня:

После извлечения квадратного корня получим
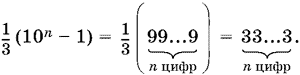
19.7. Из условия следует, что

а следовательно, (а1 − a3)² = 0, а1 = а3. Поскольку
![]()
, то а2 = а1. Таким образом, а1 = а2 = а3. Решим теперь систему уравнений
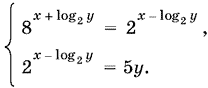
Первое уравнение можно последовательно преобразовать:
![]()
Подставив найденное значение x во второе уравнение системы, получим

Теперь можно найти x:
x = −2 log2 y = ½ log2 5.
Ответ.
![]()
19.8. Пусть q — знаменатель прогрессии. Тогда по теореме Виета
x1(1 + q) = 3, x1q²(1 + q) = 12, x1²q = A, x1²q5 = B.
Из первых двух уравнений (подстановкой первого во второе) находим q² = 4.
Так как последовательность по условию является возрастающей, то q = 2, откуда x1 = 1, что не противоречит тому, что прогрессия возрастающая.
Из двух вторых уравнений определяем А и В.
Ответ. А = 2, В = 32.
19.9. Пусть x2 = x1q, x3 = x1q². Тогда по теореме Виета, примененной к данному уравнению, имеем
x1 + x1q + x1q² = 7, x1²q + x1²q² + x1²q³ = 14.
Из первого уравнения получим x1(1 + q + q²) = 7. Это позволяет следующим образом преобразовать левую часть второго уравнения:
x1²q(1 + q + q²) = 7x1q,
откуда x1 = 2/q. Подставим выражение для x1 в первое уравнение, получим
2(1 + q + q²)/q = 7, т. е. 2q² − 5q + 2 = 0,
откуда
q1 = ½, q2 = 2.
Теперь для каждого из этих двух значений q можно найти x1. При q = 1 получим, что x1 = 4, т. е. прогрессия убывающая. Во втором случае при q = 2 имеем x1 = 1, и прогрессия — возрастающая.
Ответ. 1, 2, 4.
19.10. Из условия следует, что
![]()
Произведение n первых членов прогрессии равно
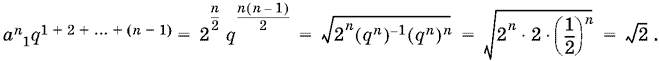
Ответ. √2.
19.11. Пусть а — цифра сотен, d — разность прогрессии. Искомое число делится на пять, если его последняя цифра либо 0, либо 5, т. е. либо а + 2d = 0, либо а + 2d = 5. Чтобы число делилось на девять, сумма его цифр должна делиться на девять. Но поскольку сумма трех цифр может изменяться от нуля до двадцати семи, имеются три возможности:
а + (а + d) + (а + 2d) = 9; 18; 27.
Последнюю возможность отбрасываем, так как число 999 не делится на пять.
Пусть а + 2d = 0. Если а + d = 3, то d = −3, а = 6. Получим число 630. Если а + d = 6, то d = −6, а = 12, что невозможно.
Пусть теперь а + 2d = 5. Когда а + d = 3, получим d = 2, а = 1, что даст число 135. Когда а + d = 6, получим d = −1, а = 7, что приводит к числу 765. Поскольку все возможности исчерпаны, задача решена.
Ответ. 630; 135; 765.
19.12. Задачу можно решить, обозначив через x цифру единиц, а через q знаменатель прогрессии. Используя условия задачи, мы придем к двум уравнениям:
100xq² + 10xq + x − 594 = 100x + 10xq + xq², (x + 1) + (xq² + 1) = 2(xq + 2).
Первое уравнение можно переписать в виде
x(q² − 1) = 6,
а второе — в виде
x(q² − 2q + 1) = 2, т. е. x(q − 1)² = 2.
Деля первое уравнение на второе, получим
q + 1/q − 1 = 3, q = 2.
Следовательно, x = 2.
Задачу можно решить перебором, если воспользоваться тем, что цифры числа образуют геометрическую прогрессию, причем цифра сотен больше пяти (так как число больше 594). Можно доказать, что имеются лишь три возможности: 842, 931 и 964. Второе и третье из этих чисел нужно отбросить, так как 931 − 594 ≠ 139 и 964 − 594 ≠ 469. Остается убедиться, что для числа 842 все условия задачи выполнены.
Требование, чтобы числа x + 1, хq + 2, хq² + 1 образовывали арифметическую прогрессию при таком решении, оказывается лишним.
Ответ. 842.
19.13. Пусть в колхозе было n комбайнов, один смог бы убрать весь урожай за x ч непрерывной работы, а при работе по плану все комбайны одновременно находились в поле y ч. Так как все комбайны могут справиться с уборкой за 24 ч, а производительность одного комбайна 1/x, то
24/x n = 1, т. е. 24n = x.
Если комбайны работают по плану, то, работая вместе, они сделали п1/xy часть всей работы. Кроме этого, первый комбайн работал n − 1 ч, второй n − 2, а (n − 1)−й работал один час. Учитывая все это, получим уравнение
n − 1/x + n − 2/x + ... + 1/x + n1/xy = 1,
или
n − 1/2n + ny = x.
Так как x = 24n, то из этого уравнения можно выразить y через n:
y = 24 − n − 1/2.
Наконец, последнее условие задачи можно записать в виде уравнения
(n + y − 7)(n − 5)1/x = 1.
Подставляя вместо x и y их выражения через n, придем к квадратному уравнению
( n + 17 − n − 1/2)(n − 5) = 242n,
т. е. n² − 18n − 175 = 0.
Решая это уравнение, найдем n1 = 25, n2 = −7. Второй корень не имеет смысла.
Ответ. 25.
19.14. Пусть братьям a, aq и aq² лет. Тогда они получат соответственно x, xq и xq² p.
Через 3 года им будет a + 3, aq + 3 и aq² + 3 лет, причем старшему окажется вдвое больше лет, чем младшему:
aq² + 3 = 2(a + 3). (1)
При дележе через 3 года младший брат получит x + 105, средний xq + 15. Чтобы узнать, сколько получит старший брат, вычтем эти деньги из всей суммы:
x + xq + xq² − (x + 105) − (xq + 15) = xq² − 120.
Так как братья делят деньги пропорционально их возрасту, то получим еще два уравнения:
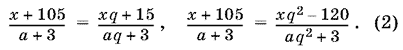
Уравнение (1) позволяет записать второе из уравнений (2) так:
2(x + 105) = xq² − 120,
т. е.
x(q² − 2) = 330. (3)
Если в (1) раскрыть скобки, а затем вынести за скобки a, то
a(q² − 2) = 3. (1′)
Сравним с уравнением (3):
x = 110a.
Первое из уравнений (2) можно переписать так:
(110a + 105)(aq + 3) = (110aq + 15)(a + 3), т. е. 5aq − 7a = 6.
Решим его совместно с уравнением (1′):

Из первого уравнения а = 6/5q − 7. Подставим во второе. После преобразований получим квадратное уравнение
6q² − 15q + 9 = 0,
откуда q1 = 3/2 , q2 = 1.
Второй корень посторонний, так как тогда всем братьям одинаковое количество лет и никто из них не может через 3 года стать вдвое старше другого.
Ответ. 12, 18, 27.
19.15. Пусть
![]()
а, b, с и
![]()
а², b², с². Другими словами, 2b = а + с и b4 = а²с². Если первое уравнение возвести в квадрат
4b² = а² + 2aс + с²,
а второе записать в виде b² = |ac|, то, сравнивая левые части этих равенств, найдем
а² + 2aс + с² = 4|ac|.
Если а и с одного знака, получаем уравнение
а² − 2aс + с² = 0, т. е. (а − с)² = 0,
откуда а = с. Следовательно, а² = с² и знаменатель прогрессии
![]()
а², b², с² равен 1. Если а и с разных знаков, получаем уравнение
а² + 6ас + с² = 0.
Разделим на а² (по условию а ≠ 0) и решим уравнение
(c/a)² + 6c/a + 1 = о
относительно c/a:
c/a = −3 ± √8.
Так как c²/a² = q², то
q² = (−3 ± √8)².
Числа а², b² и с², образующие геометрическую прогрессию, положительны. Следовательно, q > 0. Таким образом, из последнего уравнения
q2,3 = 3 + √8.
Ответ. 3 − √8; 1; −3 + √8.
19.16. При n = 1 формулы верны:
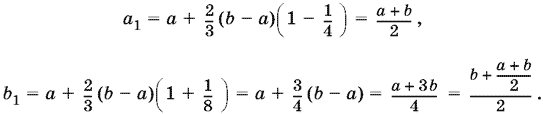
Предположим, что эти формулы верны для n = k, и докажем, что они верны для n = k + 1:

Так как
![]()
то предел последовательности равен a + ⅔(b − a) = a + 2b/3.
Ответ. a + 2b/3.
19.17. Данное уравнение равносильно совокупности двух уравнений
(8a − 3)x + (14a + 5)x = 2kπ, (14a + 5)x − (8a − 3)x = 2nπ,
или
(11a + 1)x = kπ, (3a + 4)x = nπ.
Так как по условию a > 0, то 11a + 1 ≠ 0 и 3a + 4 ≠ 0. Поэтому
xk = kπ/11a + 1, xn = nπ/3a + 4.
Значения xk и xn при k, n = 0, 1, 2, ... (по условию x ≥ 0) образуют две прогрессии с разностями
d1 = π/11a + 1, d2 = π/3a + 4
и первыми членами, равными нулю. Числа xk и xn, расположенные в порядке возрастания, составляют арифметическую прогрессию тогда и только тогда, когда их разности кратны, т. е. либо d2 = d1m при d1 ≤ d2, либо d1 = d2m при d2 ≤ d1 (m — натуральное число). Пусть, например, d1 ≤ d2. Тогда d1 — второй член новой прогрессии (первый ее член равен нулю) и d1 — разность этой прогрессии. Однако число d2, являясь членом второй прогрессии, также должно войти в новую прогрессию. Поэтому d2 = 0 + d1m = d1m. Обратно, если d2 = d1m и d1 ≤ d2, то xn = d2n = d1mn, т. е. каждый член второй прогрессии является членом первой прогрессии. Аналогичное доказательство может быть проведено для случая d2 ≤ d1.
Итак, для d1 ≤ d2 имеем
![]()
Так как m — натуральное, то 4m − 1 > 0. В свою очередь а > 0, а потому 11 − 3m > 0 и m < 11/3. Получаем три возможных значения m — 1, 2, 3 и соответствующие им значения а = 3/8, 7/5, 11/2.
Для d2 ≤ d1 получим
![]()
При натуральном m разность 11m − 3 положительна, а так как а > 0, то 4 − m > 0 или m < 4. Каждому из трех возможных значений m = 1, 2, 3 будет соответствовать свое значение а = 3/8, 2/19, 1/30.
Ответ. 1/30, 2/19, 3/8, 7/5, 11/2.