Функции - Краткий теоретический справочник - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Область определения функции

Областью определения D(y) функции у = f(x) называется множество всех значений аргумента x, для которых выражение f(x) определено (имеет смысл). Например, рассматривается функция у = sin x на отрезке [0; π]. В данном случае D(y) = [0; π], так как данной фразой функция у = sin x определена лишь на отрезке [0; π]. Если же рассматривается функция у = sin xбез каких-либо оговорок, то это означает, что D(y) = R. В этом случае говорят также, что функция у = sin x определена на всей числовой прямой. С другой стороны, пусть рассматривается функция В данной фразе также нет каких-либо оговорок относительно того, на каком числовом промежутке рассматривается функция. Вместе с тем мы видим, что эта функция не определена для x < 1, так как при x < 1 под корнем будет отрицательное число. Эта функция также не определена при x = ±2, так как при x = ±2 знаменатель обращается в нуль. Таким образом, для данной функции D(y) = [1; 2) ∪ (2; +∞).

Напомним области определения основных элементарных функций. Область определения любого многочлена — R.

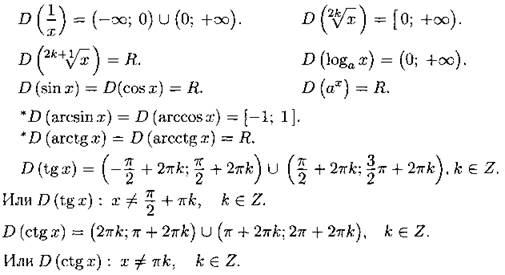
Множество значений функции

Множеством (областью) значений Е(у) функции у = f(x) называется множество всех таких чисел уо, для каждого из которых найдётся такое число x₀, что f(x₀) = у₀.

Напомним области значений основных элементарных функций.

Областью значений всякого многочлена чётной степени является промежуток [m; +∞), где m — наименьшее значение этого многочлена, либо промежуток (—∞; n], где n — наибольшее значение этого многочлена.

Областью значений всякого многочлена нечётной степени является R.

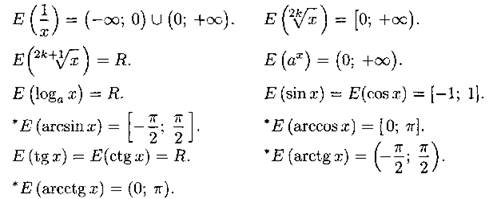
Отметим, что задания на нахождение множества значений какой-то функции решаются преимущественно двумя методами: аналитическим и алгебраическим.

Приведём одно замечание. Предположим, что функция f(x) является сложной функцией, в которой можно выделить «подфункцию» t = t(x). Тогда у = f(t) = f(t(x)). Отметим, что неважно, какой является функция t = t(x) (возрастающей, возрастающе-убывающей и т. д.). Если нам известна её область значений E(t), то при нахождении области значений функции у = f(t) = f(t(x))целесообразно считать, что t возрастает на E(t) как какой-то новый аргумент. В соответствии с этим функцию у = f(t) целесообразно считать такой, каковой она является от аргумента t на промежутке E(t). Например, пусть нам дана функция у = 2 cos х + 1. Вводим новую переменную t(x) = cos x. Понятно, что E(t) = [—1; 1]. Тогда функцию y(t) = 2t + 1 целесообразно считать линейной на промежутке [—1; 1]. Это никак не повлияет на нахождение Е(у), но, напротив, облегчит нам эту процедуру. Находим Е(у). Функция y(t) = 2t + 1 на промежутке [—1; 1] является линейной и возрастающей, поэтому Е(у) = [2(—1) + 1; 2 ∙ 1 + 1] = [-1; 3].

При решении задач аналитическим методом будем пользоваться следующими фактами.

1. Пусть f(x) — какая-то функция и где a — какое-то число или a = +∞, или а = —∞. Тогда причём при значениях x, достаточно близких к а, величина будет достаточно близкой к нулю, но вместе с тем больше нуля. В этом случае мы будем говорить, что величина стремится к нулю справа при x, стремящемся к a: В этом смысле будем употреблять запись

2. В аналогичном смысле будем употреблять также запись вида

3. Пусть теперь причём при всех x, достаточно близких к а, функция f(x) > 0. Тогда Этот факт мы будем записывать иногда в виде

4. В подобном же смысле мы будем употреблять запись

5. Ниже мы приводим записи, которые будем в дальнейшем использовать, но понимать эти записи следует не в буквальном смысле. Фактический смысл этих записей вам предлагается привести самим.

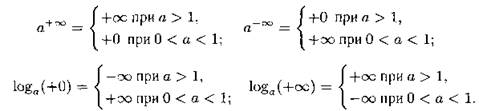
Чётность и нечётность функции

Функция у = f(x) называется чётной, если для любого х ∈ D(f) верно равенство f(—x) = f(x). График чётной функции симметричен относительно оси Оу.

Функция у = f(x) называется нечётной, если для любого х ∈ D(f) верно равенство f(—x) = —f(x). График нечётной функции симметричен относительно начала координат.

Графики элементарных функций. На рисунках 2—7 изображены графики основных элементарных функций.

Рис. 2.

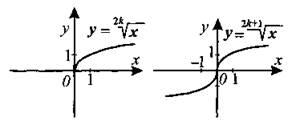
Рис. 3.

Рис. 4.

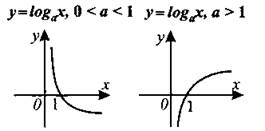
Рис. 5.

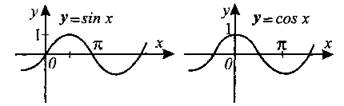
Рис. 6.

Рис. 7.

Построение графиков функций «механическими» преобразованиями

График функции у = —f(x) получен из графика функции у = f(x) отражением относительно оси Ох (см. рис. 8).

Рис. 8.

График функции у = f(—x) получен из графика функции у = f(x) отражением относительно оси Оу (см. рис. 9).

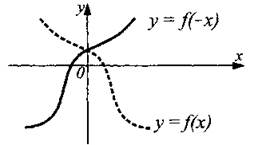
Рис. 9.

График функции у = m ∙ f(x), m > 1, получен из графика функции y = f(x) растяжением в m раз вдоль оси Оу от оси Ох (см. рис. 10).

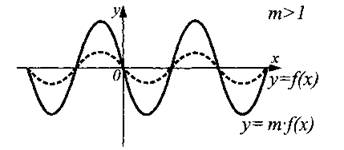
Рис. 10.

График функции y = m ∙ f(x), 0 < m < 1, получен из графика функции у = f(x) сжатием в 1/m раз вдоль оси Оу к оси Ох (см. рис. 11).

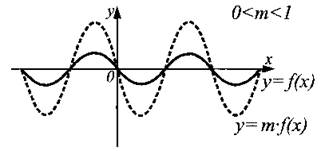
Рис. 11.

График функции у = f(kx), k > 1, получен из графика функции у = f(x) сжатием в к раз к оси Оу вдоль оси Ох (см. рис. 12).

Рис. 12.

График функции у = f(kx), 0 < k < 1, получен из графика функции у = f(x) растяжением в 1/k раз от оси Оу вдоль оси Ох (см. рис. 13).

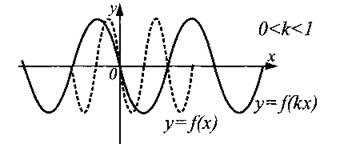
Рис. 13.

График функции у = f(x) + b получен из графика функции у = f(x) сдвигом вверх на число b при b > 0 и сдвигом вниз на число (—b) при b < 0 (см. рис. 14).

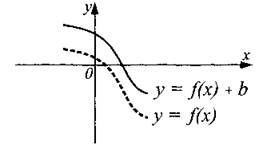
Рис. 14.

График функции у = f(x + а) получен из графика функции у = f(x) сдвигом вправо на число —а при а < 0 и сдвигом влево на число а при a > 0 (см. рис. 15).

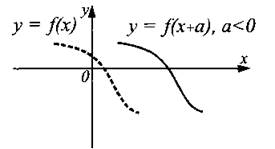
Рис. 15.

График функции у = │f(x)│ (рис. 17) получен из графика функции у = f(x) (рис. 16) отражением относительно оси Ох части этого графика, лежащей ниже оси Ох.

Рис. 16.

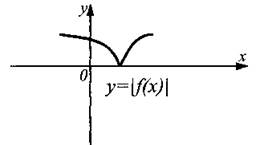
Рис. 17.

График функции у = f(│x│) (рис. 18) получен из графика функции у = f(x) (рис. 16) объединением части этого графика, лежащей правее оси Оу, с её отражением относительно оси Оу и удалением части, лежащей левее оси Оу.

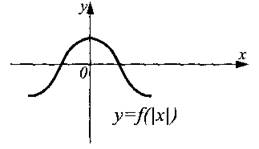
Рис. 18.

Определение производной

Пусть функция у = f(x) определена в точке х и некоторой её окрестности (интервале, содержащем точку х). Дадим аргументу х приращение ∆х (положительное или отрицательное), такое, чтобы не выйти из указанной окрестности. Найдём соответствующее приращение функции и составим отношение Если существует предел этого отношения при ∆х → 0, то этот предел называется производной функции у = f(x) в точке х и обозначается f'(x):

Таблица производных основных элементарных функций

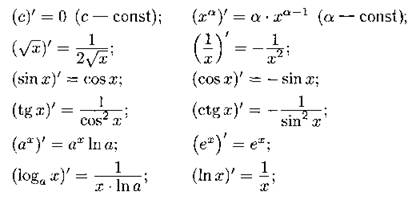
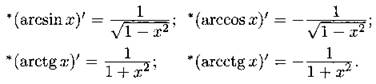
Основные правила дифференцирования

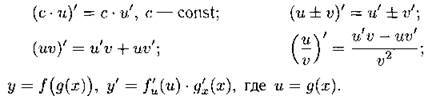
Отметим, что справедливо следующее свойство:

если функция f(x) чётна (нечётна) и дифференцируема на всей области определения, то функция f'(x) является нечётной (чётной).

Геометрический смысл производной

f'(x₀) является угловым коэффициентом касательной к графику функции у = f(x) в точке с абсциссой x₀. Напомним, что угловой коэффициент прямой равен тангенсу угла, образованного этой прямой с положительным направлением оси Ох. Уравнение касательной к графику функции у = f(x) в точке с абсциссой x₀:

Механический смысл производной

Пусть S = S(t) — уравнение зависимости пути от времени при движении какого-либо тела. Тогда S'(t) — скорость движения этого тела в момент времени t. S"(t) — ускорение движущегося тела в момент времени t.

Возрастание и убывание функции

Функция у = f(x) возрастает (убывает) на множестве А, если для любых x₁, x₂ ∈ А, таких, что х₁ < х₂, выполняется неравенство f(x₁) < f(x₂) (f(x₁) > f(x₂)).

Замечание. Если функция возрастает (убывает) на двух промежутках, из этого ещё не следует, что она возрастает (убывает) на объединении этих промежутков. Например, функция y = 1/x убывает на промежутках (—∞; 0) и (0; +∞), но она не является убывающей на области определения.

Если на каком-то промежутке функция у = f(х) возрастает (убывает) и дифференцируема на этом промежутке, то f'(х) ≥ 0 (f'(х) ≤ 0), причём равенство нулю невозможно на промежутке ненулевой длины.

Верно и обратное утверждение, которое мы сформулируем в частном случае. Именно, если на каком-то промежутке f'(х) ≥ 0 (f'(х) ≤ 0), причём равенство f'(х) = 0 достигается лишь в конечном числе точек этого промежутка, то функция у = f(х) на этом промежутке возрастает (убывает). Отсюда следует, что если производная в точке хо меняет знак с «+» на «—» (с «—» на «+»), то функция у = f(х) в этой точке меняет возрастание на убывание (убывание на возрастание). А это значит, что функция у = f(x) имеет в точке хо максимум (минимум).

Предлагаем доказать самостоятельно, что для сложной функции f(g(x)) двух непрерывных функций f(х) и g(х) справедлива данная ниже табличка, в которой «+» означает возрастание функции, а «—» — убывание.

f(x)	+	+	-	-
g(х)	+	-	+	-
f(g(x))	+	-	-	+

Наибольшее, наименьшее значения функции

Значение f(х₀) функции f(х) в точке х₀ называется наибольшим (наименьшим) значением этой функции, если для любого х из D(f) выполняется неравенство

Справедлива следующая теорема.

Дифференцируемая на (а; b) и непрерывная на [а; b] функция у = f(х) достигает своего наибольшего (наименьшего) значения на границе отрезка [а; b] или в одной из стационарных точек на интервале (а; b).

В частности, если функция удовлетворяет условиям теоремы и имеет единственную критическую точку, которая является точкой максимума (минимума), то в ней достигается наибольшее (наименьшее) значение.

Применение свойств функций при решении уравнений

Рассмотрим уравнение f(х) = g(х).

1. Пусть на ОДЗ уравнения функция f(х) возрастает, а g(х) убывает. Тогда уравнение не может иметь более одного корня.

2. Пусть функции f(х) и g(х) непрерывны на отрезке [а; b] и выполняются неравенства f(а) > g(а), f(b) < g(b). Тогда уравнение имеет по крайней мере один корень на интервале (а; b).

3. Пусть число А является наибольшим значением функции f(x) и наименьшим значением функции g(х). Тогда исходное уравнение равносильно на ОДЗ системе уравнений

Первообразная

Пусть f(x) — некоторая функция, заданная на некотором числовом промежутке А. Если функция F(x) такова, что для любого х из промежутка A F'(x) = f(x), то F(x) называется первообразной функцией для функции f(x) на промежутке А.

Отметим, что две первообразные для одной и той же функции отличаются на постоянную. И обратно, если F(x) — первообразная для f(x), то для любого с (с — const) функция F(x) + с тоже первообразная для функции f(x).

Приведём таблицу первообразных для основных элементарных функций. Буквой с везде обозначается произвольная постоянная.

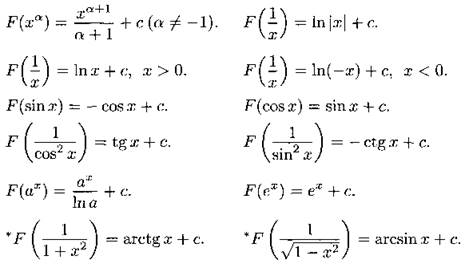
Неопределённый интеграл

Неопределённым интегралом функции f(х) называется множество всех её первообразных. Неопределённый интеграл функции f(х) обозначается через ∫f(x)dx и вычисляется по формуле ∫f(x)dx = F(x) + с, где F(x) — первообразная для функции f(x).

Кроме того, при нахождении интегралов можно пользоваться формулами:

Определённый интеграл

Определённый интеграл 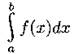можно найти по формуле 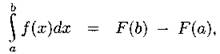если f(x) непрерывна на [а; b], a F(x) — первообразная для f(x). Для приведённой формулы используется сокращённая запись:

Справедливы формулы: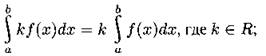

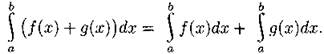
Площадь криволинейной трапеции (см. рис. 19) можно вычислить по формуле

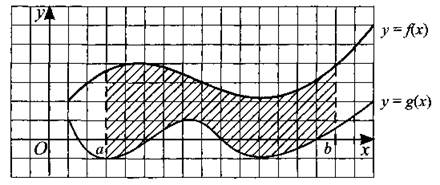
Рис. 19.