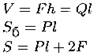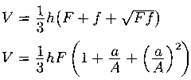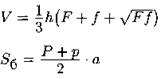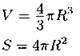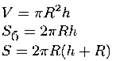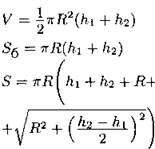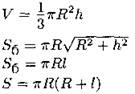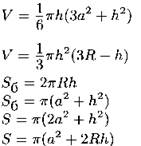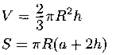Математика сборник задач для подготовки к ЕГЭ
Стереометрия - Краткий теоретический справочник - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ
Аксиомы стереометрии
Основные аксиомы
1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Факты, непосредственно связанные с аксиомами
1. Через прямую и точку, не лежащую на этой прямой, проходит единственная плоскость.
2. Через две параллельные прямые проходит единственная плоскость.
3. Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Параллельность в пространстве
1. Признак параллельности прямой и плоскости. Если прямая a параллельна некоторой прямой плоскости α, то прямая а параллельна плоскости α.
2. Если через прямую а, параллельную плоскости α, провести плоскость, пересекающую плоскость α по прямой b, то прямые а и b параллельны.
3. Если прямые а и b параллельны, а плоскость, проходящая через прямую а, пересекается с плоскостью, проходящей через прямую b, то прямая пересечения плоскостей параллельна прямым а и b.
4. Транзитивность параллельности прямых в пространстве. Если прямая а параллельна прямой b, а прямая b параллельна прямой с, то прямая а параллельна прямой с.
5. Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.
6. Если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны.
7. Транзитивность параллельности плоскостей. Если плоскость α параллельна плоскости β, а плоскость β параллельна плоскости γ, то плоскость α параллельна плоскости γ.
8. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
9. Через точку, не лежащую в плоскости, проходит единственная плоскость, параллельная данной.
Скрещивающиеся прямые
1. Признак скрещивающихся прямых. Если прямая а лежит в плоскости α, а прямая b пересекает эту плоскость в точке, не лежащей на прямой а, то а и b — скрещивающиеся прямые.
2. Через две скрещивающиеся прямые проходит единственная пара параллельных плоскостей.
3. Геометрическое место середин отрезков с концами на двух скрещивающихся прямых есть плоскость, параллельная этим прямым и проходящая через середину одного из таких отрезков.
4. Угол между скрещивающимися прямыми (угол между пересекающимися в произвольной точке М прямыми, соответственно параллельными данным) не зависит от выбора точки М.
5. Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр (отрезок с концами на этих прямых, перпендикулярный обеим прямым).
Параллельное проектирование
1. Прямая, не параллельная проектирующей, переходит в прямую.
2. Пара параллельных прямых, не параллельных проектирующей, переходит в пару параллельных прямых или в одну прямую.
3. При проектировании сохраняется отношение отрезков, лежащих на одной прямой или на параллельных прямых.
4. Наклонная пересекает плоскость в точке, лежащей на любой её параллельной проекции на эту плоскость.
5. Площадь ортогональной проекции плоского многоугольника на плоскость равна произведению площади проектируемого многоугольника на косинус угла между плоскостью этого многоугольника и плоскостью проекций.
Координаты и векторы в пространстве
1. Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.
2. Для того чтобы векторы ![]() были коллинеарны, необходимо и достаточно, чтобы выполнялось равенство
были коллинеарны, необходимо и достаточно, чтобы выполнялось равенство ![]() где k — некоторое число.
где k — некоторое число.
3. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы один из них можно было представить в виде линейной комбинации двух других (![]() где х, у — некоторые числа).
где х, у — некоторые числа).
4. Любой вектор можно единственным образом разложить по трём некомпланарным векторам.
5. Если М — середина АВ, то ![]()
6. Если М — середина АВ, а N — середина CD, то ![]()
7. Если М — точка пересечения медиан треугольника АВС, то ![]()
8. Если М — точка пересечения диагоналей параллелограмма ABCD, то ![]()
9. Координаты середины отрезка равны средним арифметическим координат его концов.
10. Свойства скалярного произведения векторов:
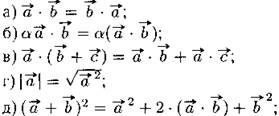
![]() причём равенство достигается тогда и только тогда, когда векторы
причём равенство достигается тогда и только тогда, когда векторы ![]() коллинеарны;
коллинеарны;
ж) ненулевые векторы ![]() перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
11. Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2) равно
![]()
12. Угол между ненулевыми векторами. Если φ — угол между ненулевыми векторами ![]() то
то
![]()
13. Уравнение плоскости, проходящей через точку М0(x0; y0; z0) перпендикулярно ненулевому вектору ![]() (вектор нормали), имеет вид
(вектор нормали), имеет вид
![]()
14. Параметрические уравнения прямой, проходящей через точку М0(x0; y0; z0) параллельно ненулевому вектору ![]() (направляющий вектор), имеют вид
(направляющий вектор), имеют вид
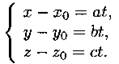
15. Уравнения прямой, проходящей через две точки A(x1; y1; z1) и B(x2; y2; z2), имеют вид
![]()
16. Прямая как пересечение двух плоскостей задаётся системой
![]()
где ![]() а коэффициенты при соответствующих неизвестных непропорциональны.
а коэффициенты при соответствующих неизвестных непропорциональны.
17. Угол между плоскостями. Если φ — угол между плоскостями, заданными уравнениями ![]() и
и ![]() то
то
![]()
18. Уравнение плоскости «в отрезках». Если плоскость пересекает оси координат в точках А(а; 0; 0), В(0; b; 0) и C(0; 0; с) (а, b, с ≠ 0), то её уравнение можно представить в виде
![]()
19. Расстояние от точки до плоскости. Если ρ — расстояние от точки М0(x0; y0; z0) до плоскости Ах + By + Cz + D = 0, то
![]()
Перпендикулярность прямой и плоскости
1. Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.
2. Если две прямые перпендикулярны одной плоскости, то они параллельны.
3. Если одна из двух параллельных прямых перпендикулярна плоскости, то вторая прямая также перпендикулярна этой плоскости.
4. Две плоскости, перпендикулярные одной прямой, параллельны.
5. Если прямая и плоскость перпендикулярны одной прямой, то они параллельны.
6. Через данную точку проходит единственная плоскость, перпендикулярная данной прямой.
7. Через данную точку проходит единственная прямая, перпендикулярная данной плоскости.
8. Теорема о трёх перпендикулярах. Прямая, лежащая в плоскости, перпендикулярна наклонной к плоскости тогда и только тогда, когда она перпендикулярна ортогональной проекции наклонной на эту плоскость.
9. Если из одной точки проведены к плоскости перпендикуляр и наклонные, то
а) перпендикуляр короче наклонных;
б) равные наклонные имеют равные ортогональные проекции;
в) большей наклонной соответствует большая ортогональная проекция;
г) из двух наклонных больше та, ортогональная проекция которой больше.
10. Теорема об угле прямой с плоскостью. Угол между наклонной и её ортогональной проекцией на плоскость меньше угла между этой наклонной и любой другой прямой плоскости.
11. Геометрическое место точек, равноудалённых от концов отрезка, есть плоскость, перпендикулярная этому отрезку и проходящая через его середину.
12. Геометрическое место точек, удалённых на данное расстояние от данной плоскости, есть две параллельные плоскости.
13. Геометрическое место точек, равноудалённых от вершин треугольника, есть прямая, проходящая через центр описанной окружности треугольника перпендикулярно его плоскости.
Двугранный угол
1. Линейный угол двугранного угла (сечение двугранного угла плоскостью, перпендикулярной его ребру) не зависит от выбора точки на ребре двугранного угла.
2. Геометрическое место внутренних точек двугранного угла, равноудалённых от его граней, есть биссекторная плоскость двугранного угла.
3. Необходимое и достаточное условие перпендикулярности плоскостей. Две плоскости перпендикулярны (образуют прямой двугранный угол) тогда и только тогда, когда одна из них проходит через перпендикуляр к другой.
4. Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, также перпендикулярной этой плоскости.
Многогранные углы
1. Плоский угол трёхгранного угла меньше суммы двух других его плоских углов.
2. Сумма плоских углов выпуклого многогранного угла меньше 360°.
Сфера. Касательная плоскость. Касающиеся сферы
1. Сечение сферы плоскостью, удалённой от центра сферы на расстояние, меньшее радиуса, есть окружность. Основание перпендикуляра, опущенного из центра сферы на секущую плоскость, есть центр этой окружности.
2. Касательная плоскость к сфере (плоскость, имеющая со сферой единственную общую точку) перпендикулярна радиусу сферы, проведённому в точку касания.
3. Касательная прямая к сфере (прямая, имеющая со сферой единственную общую точку) перпендикулярна радиусу сферы, проведённому в точку касания.
4. Центр сферы, вписанной в двугранный угол, лежит в биссекторной плоскости этого угла.
5. Отрезки касательных прямых, проведённых к сфере из одной точки, равны между собой.
6. Линия центров касающихся сфер (имеющих единственную общую точку) проходит через их точку касания.
7. Если две различные сферы имеют более одной общей точки, то они пересекаются по окружности. Плоскость этой окружности перпендикулярна линии центров данных сфер.
Пирамида
Правильная пирамида
1. Если ABCD — правильная треугольная пирамида с вершиной D, высотой DM и стороной основания a, a А1, В1 и С1 — середины сторон ВС, АС и АВ соответственно, то
а) ∠DAM = ∠DBM = ∠DCM — угол бокового ребра с плоскостью основания;
б) ∠DA1M = ∠DB1M = ∠DC1M — линейный угол двугранного угла боковой грани с плоскостью основания;
в) ∠AFB (где F — основание перпендикуляра, опущенного из вершины А основания на боковое ребро DC) — линейный угол между боковыми гранями пирамиды;
г) ![]() — высота треугольника основания;
— высота треугольника основания;
д) ![]() — ортогональная проекция бокового ребра на плоскость основания;
— ортогональная проекция бокового ребра на плоскость основания;
е) ![]() — ортогональная проекция апофемы на плоскость основания;
— ортогональная проекция апофемы на плоскость основания;
ж) C1F — общий перпендикуляр противоположных рёбер АВ и CD.
2. Противоположные рёбра правильной треугольной пирамиды попарно перпендикулярны.
3. Высота правильного тетраэдра с ребром а равна ![]()
4. Если PABCD — правильная четырёхугольная пирамида с вершиной Р, высотой РМ и стороной основания a, a A1, В1, С1 и D1 — середины сторон АВ, ВС, CD и AD соответственно, то
а) ∠PAM = ∠PBM = ∠PCM = ∠PDM — угол бокового ребра с плоскостью основания;
б) ∠PA1M = ∠PB1M = ∠PC1M = ∠PD1M — линейный угол двугранного угла боковой грани с плоскостью основания;
в) ∠BFD (где F — основание перпендикуляра, опущенного из вершины В основания на боковое ребро АР) — линейный угол между соседними боковыми гранями пирамиды;
г) ∠A1PC1 = ∠B1PD1 — линейный угол двугранного угла между противоположными боковыми гранями;
д) ![]() — ортогональная проекция бокового ребра на плоскость основания;
— ортогональная проекция бокового ребра на плоскость основания;
е) ![]() — ортогональная проекция апофемы на плоскость основания;
— ортогональная проекция апофемы на плоскость основания;
ж) FM — общий перпендикуляр диагонали BD основания и скрещивающегося с ней бокового ребра АР.
5. Боковое ребро правильной четырёхугольной пирамиды перпендикулярно скрещивающейся с ним диагонали основания.
Правильный тетраэдр. Пусть а — ребро правильного тетраэдра, a R и к — радиусы описанной и вписанной сфер, V — объём тетраэдра. Тогда
![]()
Пирамида
1. Если боковые грани треугольной пирамиды образуют равные двугранные углы с плоскостью основания, то высота пирамиды проходит либо через центр вписанной окружности, либо через центр одной из вневписанных окружностей основания.
2. Если все боковые рёбра пирамиды образуют с основанием равные углы или если все боковые рёбра равны, то высота пирамиды проходит через центр окружности, описанной около основания.
3. Теорема о медианах тетраэдра. Медианы тетраэдра (отрезки, соединяющие вершины тетраэдра с точками пересечения медиан противолежащих граней) пересекаются в одной точке и делятся ею в отношении 3 : 1, считая от вершины.
4. Если пересечь пирамиду плоскостью, параллельной основанию, то в сечении образуется многоугольник, подобный основанию.
5. В пирамиде и в конусе площади сечений, параллельных основанию, относятся как квадраты их расстояний до вершины.
Параллелепипед
1. Параллелепипед называется прямым, если его боковые рёбра перпендикулярны основанию.
2. Прямой параллелепипед, в основании которого лежит прямоугольник, называется прямоугольным.
3. Свойства диагоналей прямоугольного параллелепипеда
а) диагонали прямоугольного параллелепипеда равны;
б) квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений (длин трёх рёбер с общей вершиной).
4. Свойства граней и диагоналей параллелепипеда. Противоположные грани параллелепипеда равны и параллельны. Диагонали параллелепипеда пересекаются и делятся точкой пересечения пополам.
5. Диагональ АС1 параллелепипеда ABCDA1B1C1D1 проходит через точку пересечения медиан треугольника A1BD и делится ею в отношении 1 : 2, считая от точки А.
Площади поверхности многогранников
1. Площадь боковой поверхности призмы равна произведению периметра перпендикулярного сечения призмы на боковое ребро.
2. Площадь боковой поверхности правильной пирамиды равна площади её основания, делённой на косинус угла боковой грани с плоскостью основания.
Объёмы многогранников
1. Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
2. Объём наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
3. Объём призмы равен произведению площади основания на высоту.
4. Объём треугольной призмы равен половине произведения площади боковой грани на расстояние между этой гранью и противолежащим ей боковым ребром.
5. Объём пирамиды равен трети произведения площади основания на высоту.
6. Пирамиды с равными высотами и равновеликими основаниями равновелики.
7. Плоскость, проходящая через вершину пирамиды и прямую, лежащую в основании, делит объём пирамиды в том же отношении, в котором прямая делит площадь основания.
8. Если точки А1, B1 и С1 лежат на боковых рёбрах DA, DB и DC соответственно треугольной пирамиды ABCD или на их продолжениях, то объём пирамиды А1В1C1D1 относится к объёму пирамиды ABCD как произведение отношении ![]()
9. Отношение объёмов подобных многогранников равно кубу коэффициента подобия.
10. Объём V тетраэдра равен шестой части произведения длин двух противоположных рёбер а и b на расстояние с между ними и на синус угла (р между ними, то есть ![]()
11. Объём V тетраэдра равен двум третям произведения площадей двух граней Р и Q на синус угла φ между ними, делённому на их общее ребро а, то есть ![]()
12. А. Объём тетраэдра равен трети произведения его полной поверхности на радиус вписанной сферы.
Б. Объём многогранника, в который можно вписать сферу, равен трети произведения полной поверхности многогранника на радиус вписанной сферы.
Основные формулы
Далее V — объём тела, Sб и S — его боковая и полная поверхности.
Многогранники
|
Чертежи |
Обозначения |
Формулы |
|
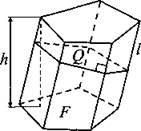
Призма
|
F — площадь основания; h — высота; l — боковое ребро; Q и Р — площадь и периметр сечения, перпендикулярного боковому ребру. |
|
|
Прямая призма
|
F и P — площадь и периметр основания; l — боковое ребро. |
|
|
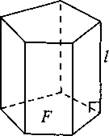
Призма, усечённая непараллельно основанию
|
l — длина отрезка OO1, соединяющего центры тяжести оснований; Q — площадь сечения, перпендикулярного к отрезку ОО1. |
V = Ql |
|
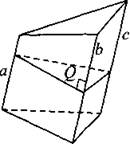
Треугольная призма, усечённая непараллельно основанию
|
а, b и с — параллельные рёбра; Q — площадь сечения, перпендикулярного к рёбрам. |
|
|
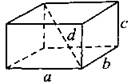
Прямоугольный параллелепипед
|
a, b и с — рёбра; d — диагональ: d2 = а2 + b2 + с2 |
|
|
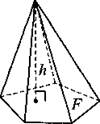
Пирамида
|
F — площадь основания; h — высота; Р — периметр основания; а — апофема (высота боковой грани правильной пирамиды). |
Правильная пирамида:
|
|
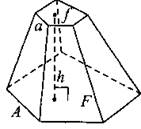
Усечённая пирамида (плоскость сечения параллельна основанию)
|
F, f — площади оснований; h — высота (расстояние между основаниями); А, а — две соответственные стороны оснований. |
|
|
Правильная усечённая пирамида
|
F, f — площади оснований; Р, р — периметры оснований; h — высота; а — апофема (высота боковой грани). |
|
Тела вращения
|
Чертежи |
Обозначения |
Формулы |
|
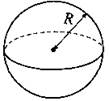
Сфера
|
R — радиус. |
|
|
Цилиндр
|
R — радиус основания; h — высота. |
|
|
Цилиндр, усечённый непараллельно основанию
|
R — радиус основания; h1 и h2 — наименьшая и наибольшая образующие. |
|
|
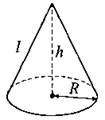
Конус
|
R — радиус основания; h — высота;
|
|
|
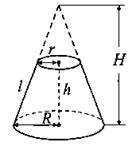
Усечённый конус
|
R и r — радиусы оснований; h — высота;
H — высота неусечённого конуса: |
|
|
Шаровой сегмент
|
h — высота сегмента; R — радиус шара;
|
|
|
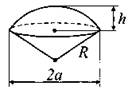
Шаровой сектор
|
h — высота сегмента; R — радиус шара; a — радиус основания сегмента. |
|