Математика сборник задач для подготовки к ЕГЭ
Вариант № 2 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ
Часть 1
В1. Сырок стоит 6 рублей 30 копеек. Какое наибольшее число сырков можно купить на 50 рублей?
В2. На рисунке 26 жирными точками показана среднесуточная влажность воздуха с 10 по 18 февраля 2011 года. По горизонтали указываются числа месяца, по вертикали — влажность воздуха в процентах. Для наглядности точки на рисунке соединены линиями. Определите по рисунку наименьшую среднесуточную влажность воздуха (в процентах) за указанный период.
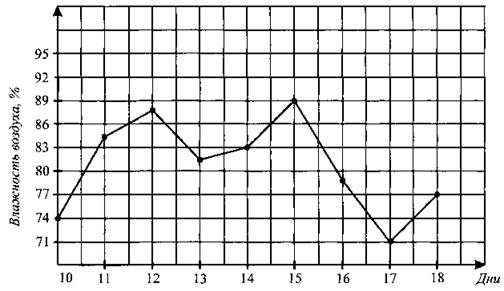
Рис. 26.
В3. На клетчатой бумаге с клетками размером 1 см х 1 см изображён треугольник (см. рис. 27). Найдите его площадь в квадратных сантиметрах.

Рис. 27.
В4. В таблице указаны цены (в рублях) на некоторые продукты питания в трёх магазинах.
|
Наименование продукта |
«Удача» |
«Вкус» |
«Высота» |
|
Рис (1 кг) |
30 |
32 |
33 |
|
Картофель (1 кг) |
20 |
18 |
16 |
|
Сыр (1 кг) |
270 |
256 |
250 |
|
Молоко (1 литр) |
30 |
28 |
31 |
|
Хлеб (батон) |
18 |
20 |
19 |
Покупателю нужно в одном из магазинов приобрести 3 батона хлеба, 2 кг риса и 0,5 кг сыра. Определите, в каком из этих магазинов покупка будет самой дешёвой. В ответ запишите стоимость покупки (в рублях).
В5. Найдите корень уравнения ![]()
В6. В треугольнике АВС угол ∠C равен 90°, sin В = 0,4. Найдите синус внешнего угла при вершине В.
В7. Найдите значение выражения ![]()
В8. На рисунке 28 изображён график функции у = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
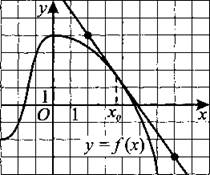
Рис. 28.
В9. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда (см. рис. 29), для которого АВ = 4, AD = 5, АА1 = 6.

Рис. 29.
В10. В группе туристов 20 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Н. полетит последним рейсом вертолёта.
В11. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 3 (см. рис. 30). Найдите объём параллелепипеда.
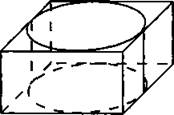
Рис. 30.
В12. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Ор, объективности публикаций Тr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5. Аналитики, составляющие формулу рейтинга, считают, что объективность ценится вчетверо, а оперативность публикаций — вдвое дороже, чем информативность и качество сайта. Таким образом, формула приняла вид ![]() Каким должно быть число А, чтобы издание, у которого все оценки наибольшие, получило рейтинг 100?
Каким должно быть число А, чтобы издание, у которого все оценки наибольшие, получило рейтинг 100?
В13. Автомобиль ехал 1,5 часа со скоростью 40 км/ч, 2,5 часа — со скоростью 60 км/ч, оставшуюся часть пути со скоростью 75 км/ч. Определите среднюю скорость автомобиля, если всего он потратил 5 часов. Ответ укажите в км/ч.
В14. Найдите наибольшее значение функции у = х3 + 5х2 - 8х + 1 на отрезке [-5; —2].
Часть 2
С1. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие отрезку [-π; π/2].
С2. В правильной четырёхугольной пирамиде SABCD с вершиной S стороны основания равны 2, а боковые рёбра равны 4. Точка К принадлежит ребру SA, причём SK : АК = 2 : 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки В и К параллельно прямой АС.
С3. Решите систему неравенств
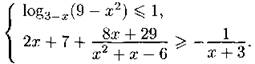
С4. Окружности радиусов 4 и 18 с центрами О1 и О2 соответственно касаются в точке Р. Прямая, проходящая через точку Р, вторично пересекает меньшую окружность в точке F, а большую в точке Е. Найдите площадь треугольника FEO1, если ∠PEO2 = 30°.
С5. Найдите все значения а, при которых уравнение ![]() имеет единственный корень.
имеет единственный корень.
С6. а) Чему равно число способов записи числа 1743 в виде ![]() где числа аi — целые, 0 ≤ аi ≤ 99, i = 0; 1; 2; 3?
где числа аi — целые, 0 ≤ аi ≤ 99, i = 0; 1; 2; 3?
б) Существует ли 10 различных чисел N таких, что их можно представить в виде ![]() где аi — целые, 0 ≤ аi ≤ 99, i = 0; 1; 2; 3, ровно 175 способами?
где аi — целые, 0 ≤ аi ≤ 99, i = 0; 1; 2; 3, ровно 175 способами?
в) Сколько существует чисел N таких, что их можно представить в виде ![]() где а* — целые, 0 ≤ аi ≤ 99, i = 0; 1; 2; 3, ровно 175 способами?
где а* — целые, 0 ≤ аi ≤ 99, i = 0; 1; 2; 3, ровно 175 способами?