Математика сборник задач для подготовки к ЕГЭ
Вариант № 12 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ
Часть 1
В1. Среди 50000 жителей города 70% не интересуются футболом. Среди интересующихся 60% смотрели по телевизору финал Лиги чемпионов. Сколько жителей города смотрели этот матч?
В2. На графике 76 показано изменение удельной теплоёмкости водного раствора некоторого вещества в зависимости от температуры. По горизонтали указывается температура в градусах Цельсия, по вертикали — удельная теплоёмкость в ![]() Определите по рисунку наименьшую возможную удельную теплоёмкость раствора на исследуемом диапазоне температур. Ответ дайте в
Определите по рисунку наименьшую возможную удельную теплоёмкость раствора на исследуемом диапазоне температур. Ответ дайте в ![]()
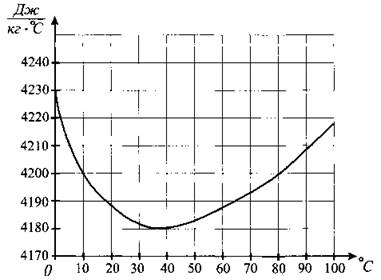
Рис. 76.
В3. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 2 и 18 (см. рис. 77).
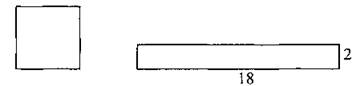
Рис. 77.
В4. В приведённой ниже таблице приведены тарифы на услуги трёх фирм такси. Предполагается поездка длительностью 80 минут. Нужно выбрать фирму, в которой заказ будет стоить дешевле всего. Сколько рублей будет стоить этот заказ в выбранной фирме?
|
Фирма такси |
Подача машины |
Продолжительность и стоимость минимальной поездки* |
Стоимость одной минуты сверх продолжительности минимальной поездки (в руб.) |
|
А |
Бесплатно |
Нет |
12 |
|
Б |
Бесплатно |
20 мин — 150 руб. |
14 |
|
В |
50 руб. |
15 мин — 50 руб. |
13 |
* Если поездка длится меньше указанного времени, она оплачивается по стоимости минимальной.
В5. Найдите корень уравнения ![]()
В6. В треугольнике АВС угол С равен 90°, АВ = 10, ВС = √19. Найдите синус внешнего угла при вершине В.
В7. Найдите значение выражения 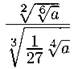 при a = 23,72.
при a = 23,72.
В8. На рисунке 78 изображён график производной функции f(x), определённой на интервале (—8; 11). Найдите количество точек максимума функции f(x) на отрезке [—7; 10].
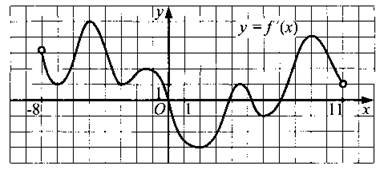
Рис. 78.
В9. В правильной треугольной пирамиде SABC точка М — середина ребра АС, S — вершина (см. рис. 79). Известно, что SM = 5, а площадь боковой поверхности равна 15. Найдите длину отрезка АВ.
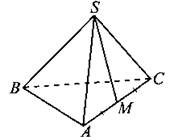
Рис. 79.
В10. Если футбольная команда А играет на домашнем стадионе, то она выигрывает у футбольной команды Б с вероятностью 0,4. Если А играет в гостях (на домашнем стадионе команды Б), то А выигрывает у Б с вероятностью 0,3. Команды А и Б играют два матча, по одному разу на домашнем стадионе каждой из них. Найдите вероятность того, что А выиграет оба матча.
В11. Объём конуса равен 20. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной (см. рис. 80). Найдите объём меньшего конуса.
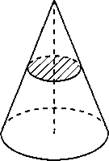
Рис. 80.
В12. Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону ![]() где t — время в минутах, ω = 20°/мин — начальная угловая скорость вращения катушки, а β = 4°/мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки р достигнет 2400°. Определите время после начала работы лебёдки, не позже которого рабочий должен проверить её работу. Ответ выразите в минутах.
где t — время в минутах, ω = 20°/мин — начальная угловая скорость вращения катушки, а β = 4°/мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки р достигнет 2400°. Определите время после начала работы лебёдки, не позже которого рабочий должен проверить её работу. Ответ выразите в минутах.
В13. Расстояние между городами А я В равно 850 км. Из города А в город В со скоростью 75 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В со скоростью 80 км/ч — второй автомобиль. На каком расстоянии от города А автомобили встретятся? Ответ дайте в километрах.
В14. Найдите наибольшее значение функции ![]() на отрезке [—4; —1].
на отрезке [—4; —1].
Часть 2
С1. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие промежутку (-4π; -5π/2).
С2. В правильной треугольной призме АВСА1В1С1 сторона основания равна 6, высота — 10. На рёбрах АС и A1B1 отмечены точки К и М соответственно так, что АК : КС = А1М : МВ1 =2 : 1. Найдите косинус угла между прямыми AC1 и КМ.
С3. Решите систему неравенств
![]()
С4. Окружность с центром О проходит через вершины А и В треугольника АВС и пересекает луч СА в точке М и луч СВ в точке N. ∠AOM = ∠BON = 60°, площадь треугольника АВС равна 9√3. Найдите расстояние от точки N до прямой АВ, если длины MN и АВ отличаются в 3 раза.
С5. Найдите все значения параметра а, при которых система ![]() имеет хотя бы одно решение.
имеет хотя бы одно решение.
С6. Разбившись на бригады, 28 школьников пошли собирать яблоки. После окончания сбора школьники каждой бригады делят между собой поровну собранные этой бригадой яблоки, а остаток от такого деления (если он есть) отправляют в общий котёл, где будет вариться компот (котёл один на все 28 человек). Всего в саду росло на деревьях 304 яблока, и все они были собраны. Какое наибольшее число яблок может оказаться в котле, если:
а) в каждой бригаде 4 человека;
б) в бригадах может быть любое количество человек (причём в разных бригадах — разное)?