Вариант № 14 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. В доме, в котором живёт Маша, 12 этажей и несколько подъездов. На каждом этаже любого подъезда находится по 3 квартиры. Маша живёт в квартире № 128. На каком этаже живёт Маша?

B2. На диаграмме (см. рис. 87) показано число посетителей сайта «Инфоновости» за каждый месяц 2010 года. По горизонтали указываются месяцы, по вертикали — число посетителей. Определите по диаграмме номер месяца, когда число посетителей сайта впервые превысило 40 тысяч человек.

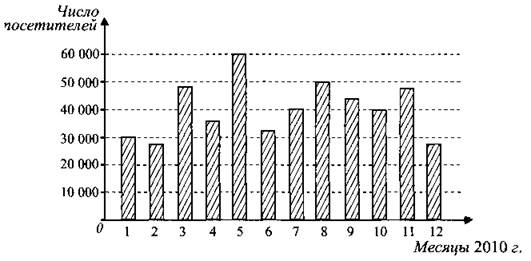
Рис. 87.

В3. Найдите диагональ квадрата, если его площадь равна 18 (см. рис. 88).

Рис. 88.

В4. В первом банке один евро можно купить за 41,2 рубля. Во втором банке 20 евро — за 819 рублей. В третьем банке 25 евро стоят 1028 рублей. Какую наименьшую сумму (в рублях) придётся заплатить за 100 евро?

В5. Найдите корень уравнения log₂ (2х) = 3.

В6. Угол АСО равен 34°, его сторона СА касается окружности с центром О (см. рис. 89). Найдите градусную величину дуги AD, заключённой нутри этого угла.

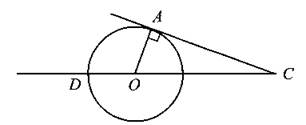
Рис. 89.

В7. Найдите значения выражения

В8. На рисунке 90 изображён график функции у = f(x), определённой на интервале (—6; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = 4 или совпадает с ней.

Рис. 90.

В9. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке О. Объём пирамиды равен 54, OS = 6. Найдите площадь треугольника АВС.

В10. Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвуют 16 шахматистов, среди которых 4 представителя России, в том числе Василий Зайцев. Найдите вероятность того, что в первом туре Василий Зайцев будет играть с каким-либо шахматистом из России.

В11. В цилиндрический сосуд налили 5000 см³ воды (см. рис. 91). Уровень воды при этом достигает высоты 24 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 18 см. Чему равен объём детали? Ответ выразите в см³.

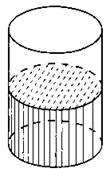
Рис. 91.

В12. Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 1 + 13t — 5t², где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее семи метров?

В13. Лодка движется по течению со скоростью 16 км/ч, при этом от города А до города В она идёт 3 часа, а обратно — 5 часов. Определите скорость течения реки. Ответ укажите в км/ч.

В14. Найдите точку минимума функции

Часть 2

С1. а) Решите уравнение

б) Найдите корни уравнения, принадлежащие промежутку [-π/2; -5π/24).

С2. В основании прямой четырёхугольной призмы ABCDA₁B₁C₁D₁ лежит прямоугольная трапеция ABCD с ∠В = 90° и основаниями АВ = 20, CD = 15, AD = 7. Найдите угол между плоскостью A₁B₁C₁ и плоскостью ADB₁, если объём призмы равен 840√/6.

С3. Решите систему неравенств

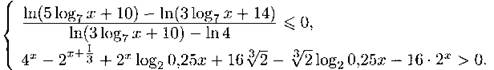
С4. К окружности с центром О проведена секущая АО и касательная АВ. Расстояние от точки А до точки касания равно 40, расстояние от А до ближайшей точки пересечения прямой и окружности равно 20. Найдите радиус окружности, которая касается прямых АВ и АО и отрезка ОВ.

С5. Найдите все значения параметра а, при которых уравнение имеет ровно 2 корня.

С6. В алфавите племени Шашашу 6 букв.

а) Сколько 6-буквенных слов можно составить, в которых все буквы различны?

б) Сколько 6-буквенных слов можно составить, в которых одна буква встречается дважды, а все остальные различны?

в) Сколько 6-буквенных слов можно составить, в которых каждая буква встречается не более 2 раз?