Вариант № 17 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. На день рождения полагается дарить букет из нечётного числа цветов. Ромашки стоят 20 рублей за штуку. У Вани есть 250 рублей. Какое наибольшее количество цветов может купить Ваня на эти деньги, чтобы поздравить Машу с Днём рождения?

В2. На диаграмме (см. рис. 101) показано число автомобилей, проданных фирмой за каждый месяц 2010 года. По горизонтали указываются месяцы, по вертикали — количество автомобилей. Определите по диаграмме номер месяца, когда впервые было продано менее 3000 автомобилей.

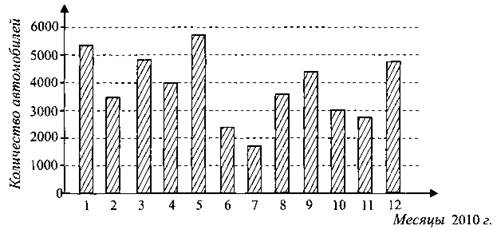
Рис. 101.

В3. На клетчатой бумаге с клетками размером 1 см х 1 см изображён треyгольник (см. рис. 102). Найдите его площадь в квадратных сантиметрах.

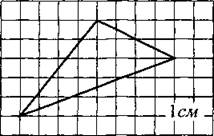
Рис. 102.

В4. Семье из трёх человек необходимо добраться из Москвы в Ростов-на-Дону. Можно доехать поездом, а можно на своей машине. Билет на поезд на одного человека стоит 1120 рублей. Автомобиль расходует 9 литров бензина на 100 км, расстояние по шоссе между этими городами составляет 1200 км, а цена бензина равна 30 рублей за литр. Сколько рублей обойдётся наиболее дешёвая поездка на троих?

В5. Найдите корень уравнения 3х² — 7х — 10 = 0. Если уравнение имеет более одного корня, то в ответе укажите меньший из них.

В6. Найдите высоту треугольника АВС, опущенную на сторону ВС (см. рис. 103), если стороны квадратных клеток равны √2.

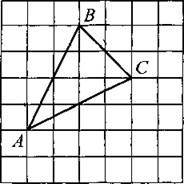
Рис. 103.

В7. Найдите tg α, если cos α = -4/√65 и a ∈ (π; 3π/2).

В8. На рисунке 104 изображён график функции у = f(x), определённой на интервале (—3; 11). Найдите сумму точек экстремума функции f(x).

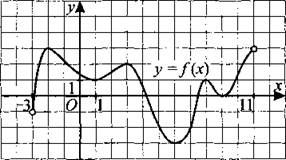
Рис. 104.

В9. Найдите тангенс угла С₂С₃В₂ многогранника, изображённого на рисунке 105. Все двугранные углы многогранника прямые.

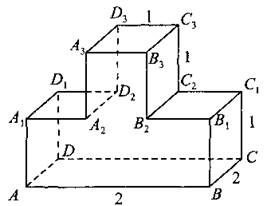
Рис. 105.

В10. Из произведённых на заводе лампочек 5% имеют дефект. При контроле качества продукции отбраковывается 90% дефектных лампочек. Остальные лампочки поступают в продажу. Найдите вероятность того, что случайно выбранная до контроля качества лампочка попадёт в продажу.

В11. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру (см. рис. 106). Объём отсечённой треугольной призмы равен 3. Найдите объём исходной призмы.

Рис. 106.

В12. При нормальном падении света с длиной волны λ = 420 нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума k связаны соотношением d sin φ = kλ. Под каким минимальным углом φ (в градусах) можно наблюдать третий максимум на решётке с периодом, не превосходящим 2520 нм?

В13. Имеется кусок сплава меди с оловом общей массой 24 кг, содержащий 45% меди. Сколько килограммов чистого олова надо прибавить к этому куску, чтобы полученный новый сплав содержал 40% меди?

В14. Найдите наибольшее значение функции у = 7ln(х + 7) — 7х + 8 на отрезке [—6,5; 0].

Часть 2

С1. а) Решите уравнение 2^1+2sin2x — 5 ∙ 2^sin2x + 2 = 0.

б) Найдите все корни уравнения, принадлежащие отрезку [-π/2; π].

С2. В кубе ABCDA₁B₁C₁D₁ отмечены точки М, N и К — середины рёбер AD, CD и ВВ₁ соответственно. Найдите площадь сечения куба плоскостью MNK, если ребро куба равно 12.

С3. Решите неравенство log_2x(5 — х) ∙ log_5-x(2x) + log_x(2x + 3) ≥ 3.

С4. В равнобедренную трапецию с основаниями АВ и CD вписана окружность с центром О. При этом угол АОВ в два раза меньше угла COD. Найдите площадь трапеции ABCD, если её основание равно 6.

С5. При каких значениях а уравнение 6^х + а² = а(2^х + 3^x) имеет корни и все они принадлежат отрезку [—1; 1]?

С6. Число 2013 представлено в виде суммы нескольких трёхзначных чисел.

а) Могут ли в этой сумме быть только слагаемые, записываемые одинаковыми цифрами?

б) Какое наибольшее число слагаемых с одинаковыми цифрами може1 быть в этой сумме?

в) Какое наибольшее число различных слагаемых с одинаковыми цифрами может быть в этой сумме?