Вариант № 21 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в час) показывает спидометр, если автомобиль движется со скоростью 40 км/ч? (Считайте, что 1 миля равна 1,6 км.)

В2. На графике (см. рис. 123) показано изменение температуры воздуха с 14 по 31 декабря. Определите по рисунку разность между наибольшим и наименьшим значениями температуры воздуха за этот период.

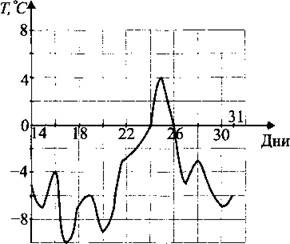
Рис. 123.

В3. Найдите сумму координат вектора (см. рис. 124).

Рис. 124.

В4. Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со средней скоростью 30 км/ч, через пункт С едет автобус со средней скоростью 43 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 64 км/ч. На рисунке 125 показана схема дорог и расстояние в километрах между пунктами по дорогам. Все три машины одновременно выехали из А. Какой автотранспорт доберётся до D позже других? В ответе укажите, сколько часов он будет находиться в дороге.

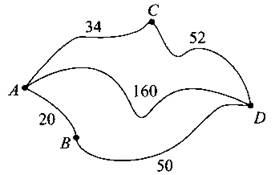
Рис. 125.

В5. Найдите корень уравнения В ответе укажете корень уравнения или сумму корней, если их несколько.

В6. Вписанные углы BAD и ADC опираются на дуги окружности, градусные величины которых равны соответственно 22° и 58° (см. рис. 126). Найдите угол АВС. Ответ дайте в градусах.

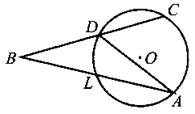
Рис. 126.

В7. Найдите cos 2α, если cos α = 0,4.

В8. На рисунке 127 изображён график функции у = f(x) и отмечены точки —4, —3, —2, —1,1. В какой из этих точек значение производной данной функции наибольшее? В ответе укажите эту точку.

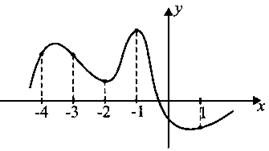
Рис. 127.

В9. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все рёбра равны 7. Найдите тангенс угла AD₁D.

В10. На рисунке 128 изображён лабиринт. Крыса заползает в лабиринт в точке «Вход». Развернуться и идти назад крыса не может, поэтому на каждом разветвлении крыса выбирает один из путей, по которому ещё не шла. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью крыса придёт к выходу А.

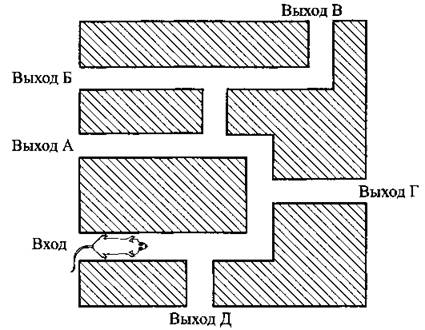
Рис. 128.

В11. Найдите объём V конуса, образующая которого равна 10 и наклонена к плоскости основания под углом 30° (см. рис. 129). В ответе укажите значение V/π.

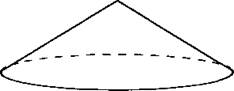
Рис. 129.

В12. В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону где Н₀ = 5 м — начальный уровень воды, t — время в секундах, прошедшее с момента открытия крана, k = 1/200 — отношение площадей поперечных сечений крана и бака, g = 10 м/с² — ускорение свободного падения. К какому моменту времени высота столба воды в баке составит не более 4,05 м? Ответ приведите в секундах.

В13. Два маляра могут выполнить работу по покраске стен помещения за 15 дней, а первый из них самостоятельно — за 20 дней. Сколько дней понадобится второму маляру, чтобы выполнить эту работу самостоятельно?

В14. Найдите наибольшее значение функции на отрезке [0; π/2].

Часть 2

С1. а) Решите уравнение sin х(3 ctg х — sin х) = 3 cos² х.

б) Найдите все корни этого уравнения, принадлежащие промежутку [-13π/2; -4π].

С2. Основанием пирамиды ABCD является треугольник АВС, для которого АВ = АС = 50 и ВС = 60. Грань BCD перпендикулярна основанию и BD = CD. Вычислите радиус шара, вписанного в пирамиду, если высота пирамиды равна 7.

С3. Решите систему неравенств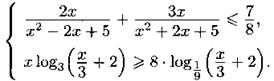

С4. В трапеции с боковыми сторонами 13 и 15 и основаниями 10 и 24 проведена диагональ. В каждый из образовавшихся треугольников вписана окружность. Найдите расстояние между точками касания вписанных окружностей с проведённой диагональю.

С5. Найдите все значения параметра а, при которых уравнение имеет ровно 2 корня.

С6. Имеется двадцать восемь литровых сосудов, содержащих 1 см³, 2 см³, 3 см³, ..., 28 см³ воды. Из сосуда А разрешается перелить в сосуд В столько воды, сколько имеется в В (при условии, что в Л не меньше воды, чем в В). Можно ли после нескольких переливаний:

а) добиться того, чтобы в сосудах вновь оказалось 1 см³, 2 см³, 3 см³, ..., 28 см³ воды, но при этом ни в одном из них не было бы первоначального её количества?

б) добиться того, чтобы в каких-то девяти сосудах оказалось по 5 см³ воды, а в остальных — 10 см³, 11 см³, 12 см³, ..., 28 см³ воды?

в) перелить всю воду в один сосуд?