Математика сборник задач для подготовки к ЕГЭ
Решение варианта № 5 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ
Часть 1
В1. Так как ![]() то наименьшее достаточное число палаток — 9.
то наименьшее достаточное число палаток — 9.
Ответ: 9.
В2. По рисунку определяем, что 17 сентября выпал 1 мм осадков.
Ответ: 1.
В3. ![]() (см. рис. 166).
(см. рис. 166).
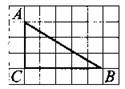
Рис. 166.
Ответ: 7,5.
В4. Автобусом: 10 мин + 1 ч 25 мин + 25 мин = 120 мин.
Электричкой: 40 мин + 55 мин + 30 мин = 125 мин.
Маршрутным такси: 35 мин + 3/4 часа + 35 мин = 115 мин.
Наименьшее возможное время в пути — 115 минут.
Ответ: 115.
B5. ![]() х = -9.
х = -9.
Ответ: -9.
В6. ![]()
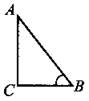
Рис. 167.
Ответ: 8.
В7. ![]()
Ответ: 13.
В8. На касательной выберем две точки A(8; 8) и В(3; 1), тогда ![]()
Ответ: 1,4.
В9. CA1 — диагональ прямоугольного параллелепипеда ABCDA1B1C1D1 (см. рис. 168).
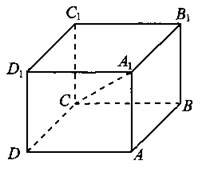
Рис. 168.

В10. Вероятность того, что поход за продуктами выпадет Диме, равна 1/5 = 0,2.
Ответ: 0,2.
В11. По условию прямоугольный параллелепипед описан около цилиндра, значит, в основании параллелепипеда — квадрат со стороной a = 2R, где R — радиус основания цилиндра; a = 2 ∙ 1 = 2. Высота параллелепипеда h равна высоте цилиндра; h = 1. Объём параллелепипеда найдём по формуле V = а2 ∙ h; V = 22 ∙ 1 = 4.
Ответ: 4.
В12. Используя формулу ![]() выразим
выразим ![]() после чего подставим наибольшие значения In = 3, Op = 3, Tr = 3 в выражение
после чего подставим наибольшие значения In = 3, Op = 3, Tr = 3 в выражение ![]()
Ответ: 0,2.
В13. Среднюю скорость автомобиля найдём по формуле ![]()
![]()
Ответ: 74.
В14. 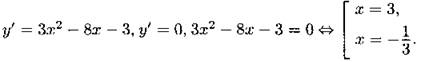
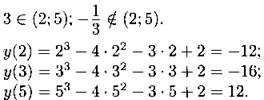
Из чисел —16, —12,12 наименьшее число —16.
Ответ: -16.
Часть 2
С1. а) Исходное уравнение равносильно уравнению ![]() 3 cos x — cos 2x = —1. Учитывая, что cos 2x = 2 cos2 x — 1, получим 3 cos х + 1 — 2 cos2 x = — 1, 2 cos2 x — 3 cos x— 2 = 0.
3 cos x — cos 2x = —1. Учитывая, что cos 2x = 2 cos2 x — 1, получим 3 cos х + 1 — 2 cos2 x = — 1, 2 cos2 x — 3 cos x— 2 = 0.
Пусть cos x = t, │t│ ≤ 1. Тогда ![]() (t = 2 не удовлетворяет условию │t│ ≤ 1),
(t = 2 не удовлетворяет условию │t│ ≤ 1), ![]() k ∈ Z.
k ∈ Z.
б) Из серии ![]() выберем корни, принадлежащие промежутку
выберем корни, принадлежащие промежутку ![]()
![]()
Из серии ![]() выберем корни, принадлежащие промежутку
выберем корни, принадлежащие промежутку ![]() таких целых k нет.
таких целых k нет.
Значит, х = 2π/3 - единственный корень из промежутка (-π/2; π].
Ответ: ![]()
С2. Пусть Я — середина АС (см. рис. 169). Заметим, что АВ = ВС, так как ABCD — квадрат, а значит, ВН — медиана и высота равнобедренного треугольника АВС, ВН ⊥ АС. Ясно, что ВН — проекция КН на плоскость ABD, следовательно, КН ⊥ АС по теореме о трёх перпендикулярах. Тогда ∠KHB — линейный угол двугранного угла между плоскостями ABD и АКС, sin ∠KHВ = 3/4.
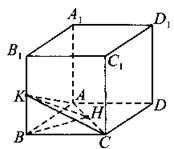
Рис. 169.
В К = КВ1 = 3, так как К — середина ВВ1. Из прямоугольного треугольника ВКН получим по определению синуса, что ![]() Тогда по теореме Пифагора ВН2= КН2 - КВ2 = 16 - 9 = 7, ВН = √7. В квадрате ABCD диагонали АС и BD равны и точкой пересечения делятся пополам. ВН проходит через середину АС и точку H, а значит, ВН лежит на BD,
Тогда по теореме Пифагора ВН2= КН2 - КВ2 = 16 - 9 = 7, ВН = √7. В квадрате ABCD диагонали АС и BD равны и точкой пересечения делятся пополам. ВН проходит через середину АС и точку H, а значит, ВН лежит на BD, ![]() В равнобедренном прямоугольном треугольнике ВНС по теореме Пифагора
В равнобедренном прямоугольном треугольнике ВНС по теореме Пифагора ![]()
Ответ: √14.
С3. Решим по отдельности каждое неравенство системы:
![]()
2) Решим второе неравенство системы, сделав замену t = х2 — 3х, получим неравенство ![]() ОДЗ: t ≥ —4. Это неравенство равносильно системе
ОДЗ: t ≥ —4. Это неравенство равносильно системе
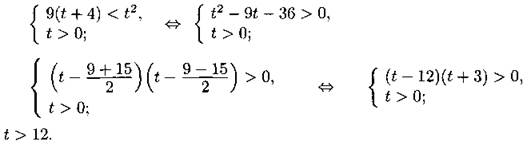
Вернёмся к исходной переменной:
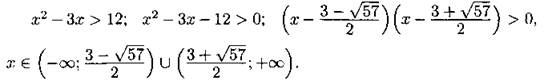
3) Учитывая, что ![]() и
и ![]() получим ответ исходной системы:
получим ответ исходной системы: ![]()
Ответ: ![]()
С4. Возможны 2 случая.
1) СМ = 3, MD = 7 (см. рис. 170). Заметим, что в четырёхугольники AKMD и КВСМ можно вписать окружности, поэтому АК + DM = AD + КМ = ВС + КМ = МС + КВ, то есть АК + 7 = КВ + 3, КВ - АК = 4.
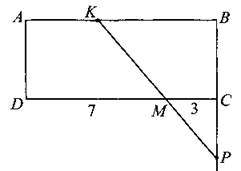
Рис. 170.
При этом АК + КВ = 10 ⇒ КВ = 7, АК = 3, откуда видно, что трапеции AKMD и ВСМК равны. Пусть AD = а, тогда радиус окружности, вписанной в AKMD, равен a/2. По условию ![]()
![]()
![]()
Заметим, что ∆МСР ~ ∆КВР (∠KPB общий, ∠MCP = ∠КВР). Значит, ![]() Пусть СР = х. Отсюда
Пусть СР = х. Отсюда 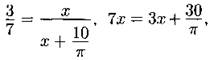
![]()
2) СМ = 7, MD = 3 (см. рис. 171). Аналогично предыдущему случаю ![]()
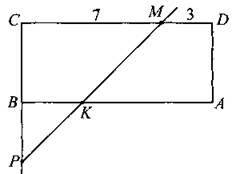
Рис. 171.
С5. Будем решать систему графически. Графиком первого уравнения является график функции ![]()
Второе уравнение задаёт окружность (см. рис. 172). В точке (—5; —5) графики касаются при любом значении а. При а < 0 центр окружности ниже прямой а = —5, а значит, это единственная общая точка. При a = 0 единственное решение — это тоже х = —5, у = —5. При a > 0 система имеет ровно 2 решения тогда и только тогда, когда указанная окружность имеет единственную общую точку с прямой у = 2х + 1, т.е. уравнение (х + 5)2 + (2х + 1 — a + 5)2 = а2 имеет единственное решение.

Рис. 172.
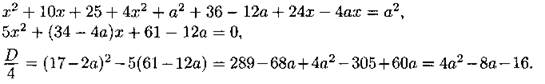
![]() Так как а > 0, а = 1 + √5. Три решения будет при а > 1 + √5.
Так как а > 0, а = 1 + √5. Три решения будет при а > 1 + √5.
Ответ: (1 + √5; +∞).
С6. а) Заметим, что все делители числа k2 разбиваются на пары (N; k2/N), где k2/N ≠ N при k ≠ N. Таким образом, число k2 имеет нечётное число делителей, в том числе при k = п!, а значит, d((n!)2) не может быть чётным числом.
б) Заметим, что если ![]() где рi — простые числа, то d(k) = (α1 + 1)(α2 + 1)...(αm + 1). Число 105 = 3 ∙ 5 ∙ 7 — раскладывается не более чем на 3 множителя, неравных 1. Если уравнение d((n!)2) = 105 имеет решение, то (n!)2 (а значит и n!) имеет не более 3 простых делителей, отсюда следует, что n ≤ 5. При n = 1 число (n!)2 имеет 1 делитель, при n = 2 число (n!)2 имеет 3 делителя, при n = 3 число (n!)2 = 36 = 22 ∙ 32 имеет (2 + 1) (2 + 1) = 9 делителей, при n = 4 число (n!)2 = 26 ∙ 32 имеет 21 делитель, при n = 5 число (n!)2 = 26 ∙ 32 ∙ 52 имеет 63 делителя. Значит, решений нет.
где рi — простые числа, то d(k) = (α1 + 1)(α2 + 1)...(αm + 1). Число 105 = 3 ∙ 5 ∙ 7 — раскладывается не более чем на 3 множителя, неравных 1. Если уравнение d((n!)2) = 105 имеет решение, то (n!)2 (а значит и n!) имеет не более 3 простых делителей, отсюда следует, что n ≤ 5. При n = 1 число (n!)2 имеет 1 делитель, при n = 2 число (n!)2 имеет 3 делителя, при n = 3 число (n!)2 = 36 = 22 ∙ 32 имеет (2 + 1) (2 + 1) = 9 делителей, при n = 4 число (n!)2 = 26 ∙ 32 имеет 21 делитель, при n = 5 число (n!)2 = 26 ∙ 32 ∙ 52 имеет 63 делителя. Значит, решений нет.
в) Так как 108 чётное число, то 2n ∙ (n!)2 не должно являться квадратом, а значит n — нечётно. Заметим, что при n = 5 верно равенство 2n ∙ (n!)2 = 211 ∙ 32 ∙ 52, а потому d(2n ∙ (n!)2) = 108. Осталось показать, что других решений нет. Пусть k1 < k2, тогда ![]() При этом все делители числа 2k1 ∙ (k1!)2 являются делителями числа
При этом все делители числа 2k1 ∙ (k1!)2 являются делителями числа ![]() это можно увидеть, считая
это можно увидеть, считая ![]() Отсюда очевидно, что
Отсюда очевидно, что ![]() Значит, при n > 5 выполняется d(2n(n!)2) > 108, а при n < 5 выполняется d(2n(n!)2) < 108.
Значит, при n > 5 выполняется d(2n(n!)2) > 108, а при n < 5 выполняется d(2n(n!)2) < 108.
Ответ: а) нет; б) нет; в) 5.