Производная функции - Функции - Алгебра и начала анализа - Базовый уровень

Вычисление производной

205. Вычислите производную функции в точке х = 0.

206. Вычислите производную функции в точке х = 0.

207. Найдите производную функции ln x — 3х² + 5х + 2 и вычислите её значение при х = 5.

Геометрический смысл производной

208. Найдите угловой коэффициент касательной, проведённой к графику производной f'(x) функции f(x) = 3ctg²x в его точке с абсциссой x₀ = π/6.

209. Функция у = f(x) определена на промежутке (—5; 5). На рисунке 214 изображён график производной этой функции. Найдите количество точек графика функции, в которых касательные наклонены под углом 120° к положительному направлению оси абсцисс.

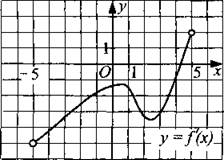
Рис. 214.

210. Функция у = f(x) определена на промежутке (—5; 5). На рисунке 215 изображён график производной этой функции. Найдите количество точек графика функции, в которых касательные наклонены под углом 150° к положительному направлению оси абсцисс.

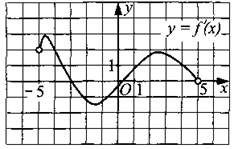
Рис. 215.

211. Функция у = f(x) определена на промежутке (—5; 5). На рисунке 216 изображён график производной этой функции. К графику функции у = f(x) провели касательные во всех точках, абсциссы которых — положительные целые числа. Укажите количество точек графика функции у = f(x), в которых проведённые касательные имеют отрицательный угловой коэффициент.

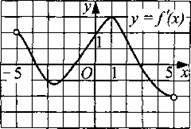
Рис. 216.

212. К графику функции у = f(x) проведена касательная в точке с абсциссой х₀ = 3. Определите градусную меру угла наклона касательной, если на рис. 217 изображён график производной этой функции.

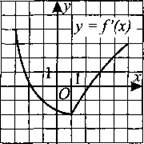
Рис. 217.

213. Найдите угловой коэффициент касательной, проведённой к графику функции у = f(x) в точке с абсциссой х₀ = —3, если на рисунке 218 изображён график производной этой функции.

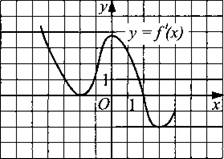
Рис. 218.

214. Найдите угловой коэффициент касательной, проведённой к графику функции у = f(x) в точке с абсциссой х₀ = 4, если на рисунке 219 изображён график производной этой функции.

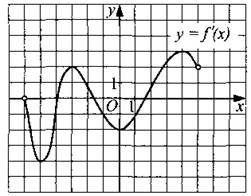
Рис. 219.

215. Найдите тангенс угла наклона касательной, проведённой к графику функции f(x) = 5х² — 7х + 2 в точке с абсциссой х₀ = 2.

216. Найдите тангенс угла наклона касательной, проведённой к графику функции f(x) = 2х² + 3х — 8 в точке с абсциссой х₀ = 3.

217. Функция у = f(x) определена на промежутке (-5; 4). На рис. 220 изображён график её производной. Найдите число касательных к графику функции у = f(x), которые наклонены под углом в 45° к положительному направлению оси абсцисс.

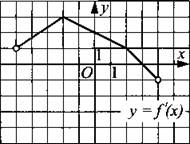
Рис. 220.

218. Функция у = f(x) определена на промежутке (—4; 5). На рисунке 221 изображён график её производной. Найдите угол наклона (в градусах) касательной к графику функции у = f(x)в точке х = 1 к положительному направлению оси Ох.

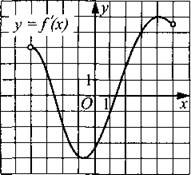
Рис. 221.

219. Функция у = f(x) определена на промежутке (—2; 4). На рисунке 222 изображён график её производной. Определите абсциссу точки, касательная в которой составляет с осью Ох угол в 45°.

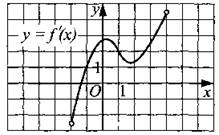
Рис. 222.

220. Функция у = f(x) определена на промежутке (—2; 7). На рис. 223 изображён график её производной. Найдите число касательных к графику функции у = f(x), которые наклонены под углом в 30° к положительному направлению оси абсцисс.

Рис. 223.

221. В точке А графика функции у = —х² + 4х + 11 проведена касательная к нему, параллельная прямой у = 1 — 2х. Найдите сумму координат точки А.

222. На рисунке 224 изображены график функции у = f(x) и касательная к нему в точке (2; —1). Найдите значение производной этой функции при x = 2.

Рис. 224.

223. Функция у = f(x) определена на промежутке (—3; 5). На рисунке 225 изображён график её производной. Найдите угол наклона касательной, проведённой к графику функции у =f(x), к положительному направлению оси Ох в точке с абсциссой x₀ = 2. Ответ укажите в градусах.

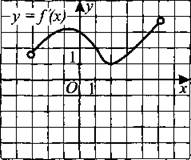
Рис. 225.

224. Найдите угловой коэффициент касательной к графику функции f(x) = e^2x+1 — 3x⁴ в точке с абсциссой х₀ = —0,5.

225. Найдите угловой коэффициент касательной к графику функции f(x) = 2е^5x-2 + 5x³ в точке с абсциссой х₀ = 2/5.

226. На рисунке 226 изображены график функции у = f(x) и касательная к этому графику в точке с абсциссой, равной 1. Найдите значение производной этой функции в точке х₀ = 1.

Рис. 226.

227. На рисунке 227 изображен график функции у = f(x) и касательная к этому графику в точке с абсциссой, равной —3. Найдите значение производной этой функции в точке х₀ = —3.

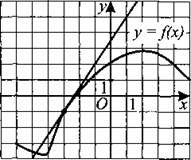
Рис. 227.

228. Прямая у = 38х — 28 параллельна касательной к графику функции у = 3х² + 8х — 2. Найдите абсциссу точки касания.

229. На рисунке 228 изображены график функции f(x) и касательная к этому графику, проведённая в точке с абсциссой х₀. Найдите значение производной f(x) в точке х₀.

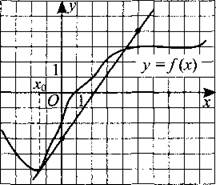
Рис. 228.

230. На рисунке 229 изображены график функции у = f(x) и касательная к этому графику, проведённая в точке с абсциссой х₀. Найдите значение производной функции f(x) в точке х₀.

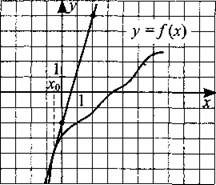
Рис. 229.

231. На рисунке 230 изображены график функции у = f(x) и касательная к этому графику, проведённая в точке с абсциссой х₀. Найдите значение производной функции f(x) в точке х₀.

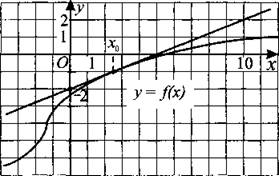
Рис. 230.

232. На рисунке 231 изображены график функции у = f(x) и касательная к этому графику, проведённая в точке с абсциссой х₀. Найдите значение производной функции f(x) в точке х₀.

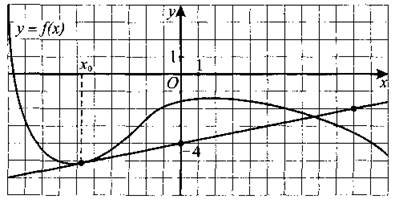
Рис. 231.

233. На рисунке 232 изображен график функции у = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 5. Найдите f'(5).

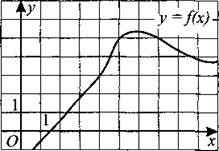
Рис. 232.

234. На рисунке 233 изображен график функции у = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 6. Найдите f'(6).

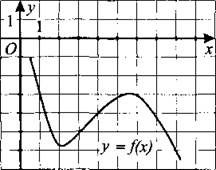
Рис. 233.

235. На рисунке 234 изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у = f(x) параллельна прямой у = 1 или совпадает с ней.

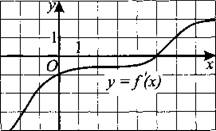
Рис. 234.

236. На рисунке 235 изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у = f(x) параллельна прямой у = 1 или совпадает с ней.

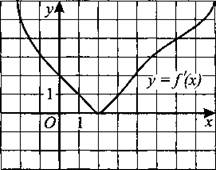
Рис. 235.

237. Прямая у = 3х — 10 параллельна касательной к графику функции у = х² + 5х — 7. Найдите абсциссу точки касания.

238. Прямая у = — х — 3 является касательной к графику функции у = х³ — 3,5x² + х - 1. Найдите абсциссу точки касания.

239. На рисунке 236 изображён график функции у = f(x), определённой на промежутке [—8; 7]. Определите количество целых точек, в которых производная функции f(x) положительна.

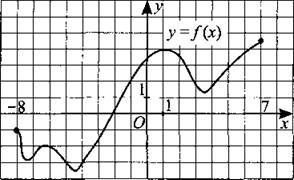
Рис. 236.

240. На рисунке 237 изображён график функции у = f(x), определённой на промежутке [—8; 7]. Найдите количество точек, в которых касательная к графику функции параллельна прямой у = —15.

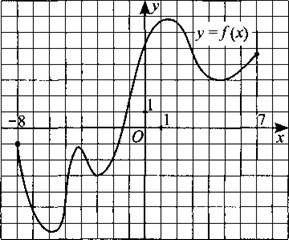
Рис. 237.

241. На рисунке 238 изображён график производной функции у = f(x), определённой на интервале (—8; 7). В какой точке отрезка [—7; —3] функция f(x) принимает наименьшее значение?

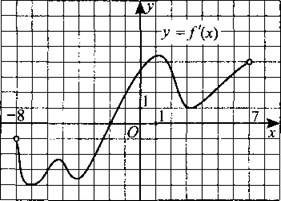
Рис. 238.

242. На рисунке 239 изображён график производной функции у = f(x), определённой на интервале (—8; 7). Найдите количество точек, в которых касательная к графику функции f(x)параллельна прямой у = —х + 2 или совпадает с ней.

Рис. 239.

243. На рисунке 240 изображён график производной функции у = f(x), определённой на интервале (—7; 7). Определите, в какой точке отрезка [2; 6] функция f(x) принимает наибольшее значение.

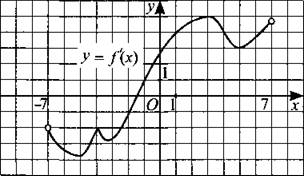
Рис. 240.

244. На рисунке 241 изображён график производной функции у = f(x), определённой на интервале (—7; 7). Найдите точку экстремума функции f(x) на интервале (—1; 5).

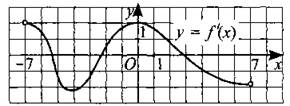
Рис. 241.

245. На рисунке 242 изображён график производной функции у = f(x), определённой на интервале (—8; 8). Найдите количество точек, в которых касательная к графику функции f(x)параллельна прямой у = —3x + 5 или совпадает с ней.

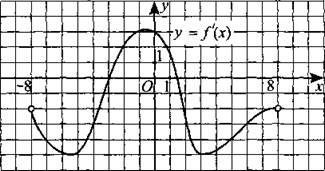
Рис. 242.

246. На рисунке 243 изображён график функции у = f(x), определённой на промежутке [—6; 6]. Определите количество целых точек, в которых, производная функции f(x) отрицательна.

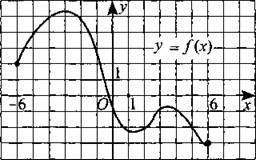
Рис. 243.

247. На рисунке 244 изображён график производной функции у = f(x), определённой на интервале (—6; 7). В какой точке отрезка [—4; 1] функция f(x) принимает наибольшее значение?

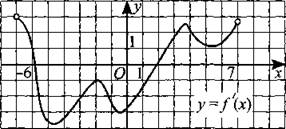
Рис. 244.

248. На рисунке 245 изображён график производной функции у = f(x), определённой на интервале (—7; 7). Найдите количество точек максимума функции f(x) на интервале (—6; 5).

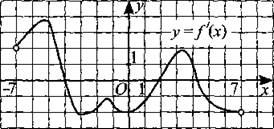
Рис. 245.

249. На рисунке 246 изображён график производной функции у = f(x), определённой на интервале (—7; 7). Найдите промежутки убывания функции у = f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

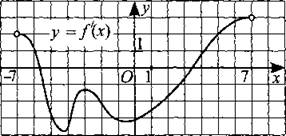
Рис. 246.

250. На рисунке 247 изображён график функции у = f(x), определённой на интервале (—3; 10). Укажите количество точек, в которых касательная к графику функции f(x) параллельна прямой у = 15.

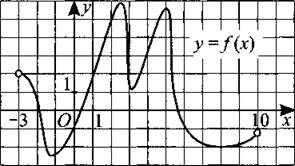
Рис. 247.

251. На рисунке 248 изображён график функции у = f(x), определённой на промежутке [—3; 10]. Найдите сумму абсцисс точек экстремума функции f(x).

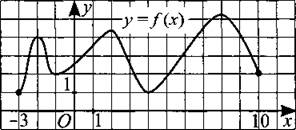
Рис. 248.

252. На рисунке 249 изображён график производной функции у = f(x), определённой на интервале (—3; 10). Найдите количество точек максимума функции f(x) на отрезке [—2; 9].

Рис. 249.

253. На рисунке 250 изображён график производной функции у = f(x), определённой на интервале (—9; 3). Найдите количество точек минимума функции f(x) на отрезке [—7; 2].

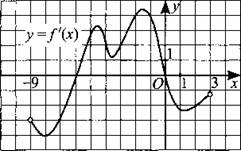
Рис. 250.

254. На рисунке 251 изображён график функции у = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

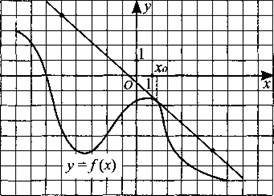
Рис. 251.

255. Функция у = f(x) задана на отрезке [—4; 4]. На рисунке 252 изображён график этой функции. Найдите наибольшую из длин промежутков возрастания функции.

Рис. 252.

256. Функция у = f(x) задана на промежутке [—4; 6]. На рисунке 253 изображён график этой функции. Найдите наибольшую из длин промежутков убывания функции.

Рис. 253.

257. На рисунке 254 изображён график функции у = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке х₀.

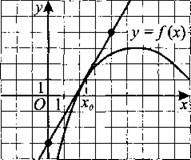
Рис. 254.

258. На рисунке 255 изображён график функции у = f(x), определённой на интервале (—7; 7). Определите количество целых точек, в которых производная функции отрицательна.

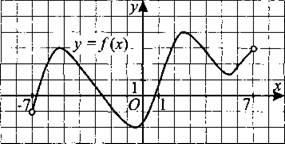
Рис. 255.

259. На рисунке 256 изображён график функции у = f(x), определённой на интервале (—8; 6). Найдите количество точек, в которых производная функции f(x) равна 0.

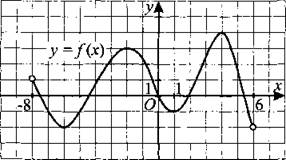
Рис. 256.

260. На рисунке 257 изображён график производной функции f(x), определённой на интервале (—9; 10). Найдите количество точек экстремума функции f(x) на отрезке [—6; 8].

Рис. 257.

261. На рисунке 258 изображён график производной функции f(x), определённой на интервале (—4; 10). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

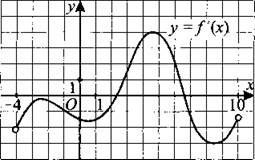
Рис. 258.

262. На рисунке 259 изображён график производной функции f(x), определённой на интервале (—10; 5). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

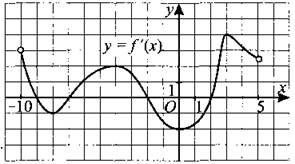
Рис. 259.

263. Прямая у = 9х + 5 является касательной к графику функции у = —х² + bх — 11. Найдите 6, учитывая, что абсцисса точки касания больше 1.

264. Прямая у = 3х — 2 параллельна касательной к графику функции у = х² + 4х — 5. Найдите абсциссу точки касания.

265. Прямая у = 3х + 30 параллельна касательной к графику функции у = х³ + 5х² — 5х — 18. Найдите наименьшую из возможных абсцисс точек касания.

266. На рисунке 260 изображён график у = f'(x) — производной функции f(x), определённой на интервале (—5; 8). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

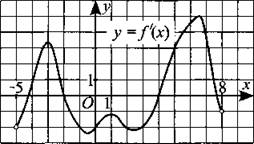
Рис. 260.

267. На рисунке 261 изображён график производной функции f(x), определённой на интервале (—5; 11). Найдите количество точек минимума функции f(x), принадлежащих отрезку [—4; 10].

Рис. 261.

268. На рисунке 262 изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены семь точек: x₁, x₂, ..., x₇. Среди этих точек найдите все точки, в которых производная функции f(x) отрицательна. В ответ запишите количество найденных точек.

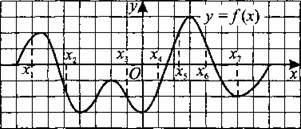
Рис. 262.

269. Прямая у = —х + 5 параллельна касательной к графику функции у = х³ + 3x² + 2x + 6. Найдите абсциссу точки касания.

270. На рисунке 263 изображён график у = f'(x) — производной функции f(x), определённой на интервале (—6; 7). В какой точке отрезка [—4; 5] функция f(x) принимает наименьшее значение?

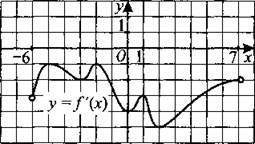
Рис. 263.

271. На рисунке 264 изображён график дифференцируемой функции у = f(x), определённой на интервале (—6; 10). На оси абсцисс отмечены шесть точек: x₁, x₂, x₃, x₄, x₅, x₆. Среди этих точек найдите все точки, в которых производная функции f(x) равна нулю. В ответ запишите количество найденных точек.

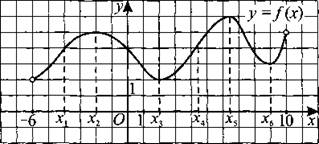
Рис. 264.

272. На рисунке 265 изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены восемь точек x₁, x₂, ..., x₈. Среди этих точек найдите все точки, в которых производная функции f(x) положительна. В ответ запишите количество найденных точек.

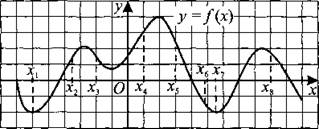
Рис. 265.

273. На рисунке 266 изображены график функции f(x) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(x) в точке х₀.

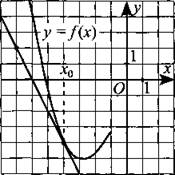
Рис. 266.

274. На рисунке 267 изображён график у = f'(x) — производной функции f(x), определённой на интервале (—6; 6). Найдите количество точек, в которых касательная к графику функцииf(x) параллельна прямой у = 2х — 8.

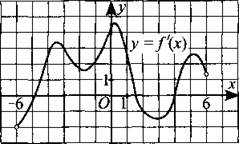
Рис. 267.

275. На рисунке 268 изображён график функции у = f(x) и касательная к этому графику в точке x₀. Уравнение касательной у = 2х — 6. Найдите значение производной функции в точке x₀.

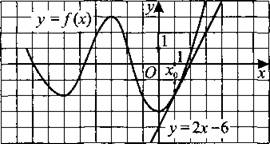
Рис. 268.

276. На рисунке 269 изображён график функции у = f(x), определённой и дифференцируемой на интервале (—6; 7). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у = 4.

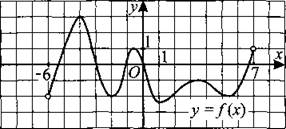
Рис. 269.

277. На рисунке 270 изображён график у = f'(x) — производной функции f(x), определённой на интервале (—6; 6). Найдите количество точек максимума функции f(x) на отрезке [—5; 3].

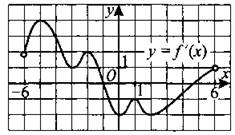
Рис. 270.

278. На рисунке 271 изображён график производной функции у = f(x), определённой на интервале (—9; 4). В какой точке отрезка [—6; 3] функция f(x) принимает наименьшее значение?

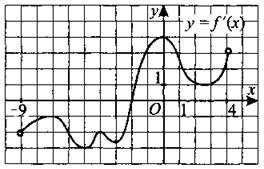
Рис. 271.

279. На рисунке 272 изображён график у = f'(x) — производной функции f(x), определённой на интервале (—9; 7). Найдите количество точек максимума функции f(x) на отрезке [—8; 6].

Рис. 272.

280. На рисунке 273 изображены график функции у = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рис. 273.

281. На рисунке 274 изображён график у = f'(x) — производной функции f(x), определённой на интервале (-4; 7). В какой точке отрезка [-2; 6] функция f(x) принимает наибольшее значение?

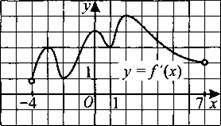
Рис. 274.

282. На рисунке 275 изображён график функции у = f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

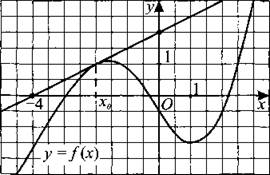
Рис. 275.

Физический смысл производной

283. Точка движется по координатной прямой согласно закону x(t) = 1,5t² — 3t + 7, где x(t) — координата в момент времени t. В какой момент времени скорость точки будет равна 12?

284. Точка движется по координатной прямой по закону x(t) = 0,75t² + t — 7, где x(t) — координата точки в момент времени t. В какой момент времени скорость точки будет равна 19?

285. Точка движется по координатной прямой согласно закону x(t) = —2t² + 20t — 7, где x(t) — координата точки в момент времени t. В какой точке координатной прямой произойдет мгновенная остановка?

286. На рисунке 276 представлены график движения тела и касательная к графику в момент времени t = 5. Определите по графику скорость движения тела (в км/ч) в этот момент времени.

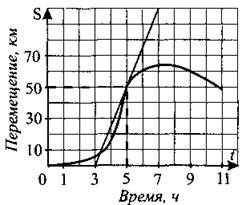
Рис. 276.

287. На рисунке 277 представлены график движения тела и касательная к графику в момент времени t = 8. Определите по графику скорость движения тела (в км/ч) в этот момент времени.

Рис. 277.

288. Перемещение материальной точки задано функцией у = S(t) на промежутке [0; 8]. На рисунке 278 изображён график её производной. Найдите момент времени, в который скорость данной точки была равна 2.

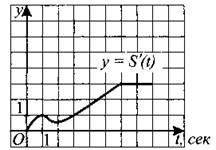
Рис. 278.

289. Перемещение материальной точки задано функцией у = S(t) на промежутке [0; 8]. На рисунке 279 изображён график её производной. Найдите момент времени, в который скорость данной точки была равна 3.

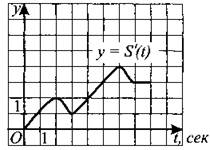
Рис. 279.

290. Мотоциклист в первые 5 с движения проезжал расстояние (в метрах), которое можно описать формулой S(t) = t³ + 3t. Найдите его ускорение в момент времени t = 1 (в м/с²).

291. При проведении испытаний нового скоростного болида в первые 6 с его движения скорость изменялась по формуле v(t) = 36t — 3t² в метрах в секунду. Какое расстояние прошёл болид за это время? (Ответ укажите в метрах.)

292. Ребёнок на санках в первые 4 с движения с горки проезжал расстояние, заданное формулой Найдите его ускорение в момент времени t = 3.

293. При метании бумеранга его скорость изменялась по формуле v(t) = 9t — t² в метрах в секунду. Найдите расстояние, которое преодолел бумеранг, если он был в движении 9 секунд. (Ответ укажите в метрах.)

294. Материальная точка движется прямолинейно по закону x(t) = 4t² — 34t + 5 (х — расстояние от точки отсчёта в метрах, t — время в секундах, измеряемое с начала движения). Найдите её скорость (в м/с) в момент времени t = 9 с.

295. Материальная точка движется прямолинейно по закону x(t) = 0,4t³ — 2t² + t (х — расстояние от точки отсчёта в метрах, t — время в секундах, измеряемое с начала движения). Найдите её скорость (в м/с) в момент времени t = 5 с.

296. Материальная точка движется прямолинейно по закону где х — расстояние от точки отсчёта в метрах, t — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени t = 2 с.

297. Материальная точка движется прямолинейно по закону где x — расстояние от точки отсчёта в метрах, t — время в секундах, прошедшее с начала движения. В какой момент времени (в секундах) скорость точки была равна 4 м/с?

298. На рисунке 280 изображена зависимость скорости некоторой материальной точки от времени. На оси абсцисс откладывается время t в секундах, на оси ординат — скорость v в метрах в секунду. Определите, сколько раз за время движения ускорение точки обращалось в ноль (начало и конец движения не учитывайте).

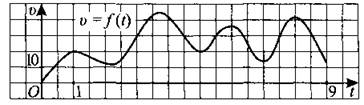
Рис. 280.

Наибольшее, наименьшее значение функции. Монотонность функции, экстремумы

299. Найдите наибольшее значение функции

300. Найдите наименьшее значение функции на отрезке [—6; 0].

Найдите наибольшее значение функции (301—302):

301. f(x) = х — log₂ х на отрезке [1/2; 2].

302. у = (х - 4)²(х - 1) на отрезке [1,5; 4,5].

Найдите наименьшее значение функции (303—304):

303. на отрезке [0; 4].

304. у = 2х³ + 2х² — 10х + 1 на отрезке [—1; 2].

Найдите наибольшее значение функции (305—306):

305. на отрезке [0; 2].

306. f(x) = 3(5x — 4)² — (5x — 4)³ при │2х — 3| ≤ 1.

307. Найдите наименьшее значение функции f(x) = 4(2x — 3)³ + (2х — 3)⁴ при │2х + 1| ≤ 1.

308. Найдите наибольшее значение функции у = —x³ + 3x + 5 на отрезке [-1; 2].

309. Найдите наименьшее значение функции у = х³ — 3х + 8 на отрезке [-3; 2].

310. Найдите наибольшее значение функции на отрезке [-5; -3].

311. Найдите наибольшее значение функции на отрезке [-2π/3; 0].

312. Найдите наибольшее значение функции на отрезке [-2π/3; 0].

313. Найдите наибольшее значение функции у = 4ctgx + 4х + 3 — 2π на отрезке [-π/2; 3/4π].

314. Найдите наибольшее значение функции на отрезке [-π/4; π/2].

315. Найдите точку минимума функции

316. Найдите наименьшее значение функции на отрезке [1; 7].

317. Найдите точку максимума функции

318. Найдите наименьшее значение функции на отрезке [7; 8].

319. Найдите наименьшее значение функции на отрезке [10; 12].

320. Найдите наименьшее значение функции на отрезке [5; 7].

321. Найдите наибольшее значение функции на отрезке [0; π/2].

322. Найдите наибольшее значение функции на отрезке [0; π/2].

323. Найдите наименьшее значение функции у = 6 cos x — 10x + 1 на отрезке [-3π/2; 0].

324. Найдите наименьшее значение функции у = 5 cos x — 7x + 4 на отрезке [-3π/2; 0].

325. Найдите наибольшее значение функции у = 15x — 4 sin x + 6 на отрезке [-π/2; 0].

326. Найдите наименьшее значение функции у = 2 sin x — 8x + 3 на отрезке [-π/2; 0].

327. Найдите наименьшее значение функции у = 2 sin x — 3x — 2 на отрезке [-3π/2; 0].

328. Найдите наибольшее значение функции на отрезке [-5π/6; 0].

329. Найдите наибольшее значение функции у = 6 tg x — 2x + 3 на отрезке [-π/4; 0].

330. Найдите наименьшее значение функции у = 7 tg x — 2x + 5 на отрезке [0; π/4].

331. Найдите точку минимума функции

332. Найдите точку минимума функции

333. Найдите наименьшее значение функции у = 6x — log₂(x + 6)² на отрезке [-5,5; 0].

334. Найдите наименьшее значение функции у = 8х — log₂(x + 3)² на отрезке [-2,5; 0].

335. Найдите наименьшее значение функции у = 5x — 5 ln(x + 4) + 2 на отрезке [—3; 0].

336. Найдите наименьшее значение функции у = 3x — ln(x + 2)³ на отрезке [-1,5; -1].

337. Найдите наибольшее значение функции на отрезке [1/2; 2].

338. Найдите наименьшее значение функции у = 2^2х + 2^х — 2 на отрезке [-1; 2].

339. Найдите наибольшее значение функции у = 6 ln(x + 6) — 6х + 11 на отрезке [-5,5; 0].

340. Найдите наименьшее значение функции у = 6 + 27х — х³ на отрезке [-3; 4].

341. Найдите наибольшее значение функции у = 5 + 6x — х² на отрезке [-2; 4].

342. Найдите точку минимума функции у = 15х² — х³.

343. Найдите точку максимума функции у = 15х² — х³.

344. Найдите точку максимума функции у = (27 — х)е^х+27.

345. Найдите наименьшее значение функции на отрезке [1; 8].

346. Найдите точку максимума функции

347. Найдите точку максимума функции

348. Найдите наибольшее значение функции на отрезке [1; 7].

349. Найдите точку минимума функции у = (2 — х)²е^5-х.

350. Найдите точку максимума функции у = (х² — 10x + 17)е^x+2.

351. Найдите наибольшее значение функции у = х² — 8х + 6 ln x + 19 на отрезке [15/17; 19/17].

352. Найдите наименьшее значение функции у = 3 + 24х — 2х² — 20 ln х на отрезке [1/7; 13/7].

353. Найдите точку максимума функции у = ln(х + 5)⁴ — 10х.

354. Найдите точку минимума функции у = 5 + log₄ (х² — 8х + 21).

355. Найдите наименьшее значение функции на отрезке [-π/4; π/4].

356. Найдите наибольшее значение функции на отрезке [0; π/2].

357. Найдите наибольшее значение функции у = (10 — х)е^х-9 на отрезке [8; 10].

358. Найдите наименьшее значение функции у = (4х² + 24х — 24)е^x на отрезке [-1; 2].

359. Найдите точку минимума функции у = 2х³ – 150x + 11.

360. Найдите точку максимума функции у = 17 — 2х^3/2 + 9х.

361. Найдите наибольшее значение функции

362. Найдите наибольшее значение функции на отрезке [4; 8].

363. Найдите точку максимума функции

364. Найдите точку минимума функции

365. Найдите точку минимума функции у = (4х — 3) sin х + 4 cos х — 4, принадлежащую промежутку (0; π/2).

366. Найдите точку максимума функции у = 2 sin х — (2х — 7) cos x + 7, принадлежащую промежутку (π; 3π/2).

367. Найдите наименьшее значение функции у = 16х — ln(8x) + 4 на отрезке [1/8; 1/3].

368. Найдите наименьшее значение функции у = 10 ln(х + 3) — 4х + 2 на отрезке [-2; -0,5].