Уравнения - Краткий теоретический справочник - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Уравнения с одним неизвестным

Напомним, что в соответствии с [1], уравнением называется равенство, содержащее неизвестное, обозначаемое буквой. Пользуясь понятием функции, можно сказать, что уравнение (с одним неизвестным) — это пара функций от одной и той же переменной х, соединённых знаком равенства:

f(x) = g(х).

Областью допустимых значений (ОДЗ) данного уравнения называется пересечение области определения функций f(x) и g(х):

D(f)∩D(g).

Число а называется корнем (или решением) данного уравнения, если при подстановке в уравнение вместо каждого вхождения х числа а уравнение обращается в верное числовое равенство: f(а) = g(а).

Существуют эквивалентные определения корня уравнения, в которых требуется принадлежность числа а ОДЗ исходного уравнения.

Решить уравнение — это значит найти все его корни или доказать, что данное уравнение корней не имеет. Отметим, что если мы нашли подбором какие-то корни уравнения и доказали, что других корней у данного уравнения быть не может, то тем самым мы уравнение решили.

Два уравнения называются равносильными, если множества их корней совпадают. Уравнение А является следствием уравнения В, если все корни уравнения В являются корнями уравнения А (но, быть может, среди корней уравнения А есть такие, которые не являются корнями В).

Преобразование уравнения называется равносильным, если преобразуемое уравнение равносильно исходному.

1. Если при решении уравнения вы производили лишь равносильные преобразования, то для найденных корней нет нужды делать проверку.

2. Если вы нашли ОДЗ и в пределах ОДЗ производили равносильные преобразования уравнения, то проверку также делать не нужно, но необходимо выяснить, входят ли найденные корни в ОДЗ.

3. Если не все преобразования были равносильными, но каждое уравнение было следствием предыдущего, то необходимо сделать проверку.

Отметим, что очень часто находить ОДЗ нецелесообразно, если экономнее (по времени) найти «корни» (среди которых, быть может, есть лишние) и сделать проверку.

Всё сказанное в отношении проверки справедливо с чисто математической точки зрения. То есть, если все ваши преобразования были равносильны, то приводить в конце решения проверку нет необходимости. И в этом случае (при наличии соответствующей оговорки) ваше решение будет смотреться более грамотным с точки зрения математики.

Но совсем иное дело, если речь идёт о самоконтроле. Здесь мы рекомендуем делать в некоторых случаях не одну, а несколько проверок.

*Полезные неравенства

Отметим, что при решении уравнений (и неравенств) иногда бывают полезны следующие неравенства, истинные для а ≥ 0, b ≥ 0:

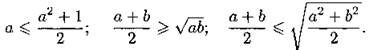
Равенства достигаются при а = b (в первом случае при а = 1).

Полезны также некоторые их следствия:

Равенства достигаются при а = 1 в первом случае и при а = —1 во втором.

Системы уравнений с двумя неизвестными

Уравнением с двумя неизвестными х и у называется пара функций от двух переменных (х и у), соединённых знаком равенства:

f(x, y) = g(x, y).

Решением такого уравнения называется всякая пара чисел (x₀, y₀), подстановка которых в уравнение вместо соответствующих неизвестных обращает это уравнение в верное числовое равенство.

Системой двух уравнений с двумя неизвестными называется пара уравнений с двумя неизвестными:

Решением системы называется всякая пара чисел (х₀, y₀), являющаяся решением и первого, и второго уравнений системы.

Решить систему — это значит найти все её решения или доказать, что система решений не имеет.

Системы линейных уравнений

Пусть дана система

1. Система имеет единственное решение тогда и только тогда, когда a₁b₂ - a₂b₁ ≠ 0.

2. Система имеет бесконечное множество решений тогда и только тогда, когда

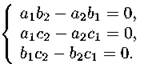
3. Система не имеет решений тогда и только тогда, когда a₁b₂ - a₂b₁ = 0, но a₁c₂ - a₂c₁ ≠ 0 или b₁c₂ - b₂c₁ ≠ 0.