Поурочные разработки по геометрии 10 класс
Скрещивающиеся прямые - ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) ввести определение скрещивающихся прямых;
2) ввести формулировку и уметь доказать признак и свойство скрещивающихся прямых.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Анализ самостоятельной работы
Сообщение итогов работы, анализ распространенных ошибок.
III. Изучение нового материала
Были рассмотрены два случая расположения прямых в пространстве. (a ∩ b; а || b). Общее для них: они лежат в одной плоскости (рис. 1, 2).
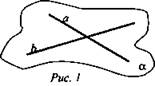
a ∩ b
(по следствию из аксиомы)
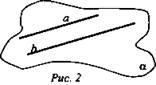
а || b
(по определению параллельных прямых)
Дан куб ABCDA1B1C1D1 (рис. 3).
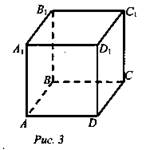
1. Являются ли параллельными прямые А1А и DD1; АА1 и CC1? Ответ обоснуйте. (А1А || DD1 как противоположные стороны квадрата или лежат в одной плоскости и не пересекаются). (А1А || DD1 и DD1 || CC1 ⇒ A1A || CC1 по теореме о трех параллельных прямых).
2. Являются ли АА1 и DC параллельными? Они пересекаются? Значит, в пространстве есть прямые, которые не пересекаются и не являются параллельными, так как они не лежат в одной плоскости. Такие прямые называются скрещивающимися.
Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Обратить внимание учеников на то, что условие «не лежат в одной плоскости» означает, что не существует плоскости, содержащей эти прямые. Именно на этом построено доказательство признака скрещивающихся прямых.
Теорема (признак скрещивающихся прямых)
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Дано: АВ ⊂ α, CD ∩ α = С, С ∉ АВ (рис. 4).
Доказать, что АВ скрещивается с CD.
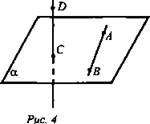
Доказательство:
Допустим, что CD и АВ лежит в одной плоскости. Пусть это будет плоскость β.
![]()
Плоскости совпадают, чего быть не может, так как прямая CD пересекает α. Плоскости, которой принадлежат АВ и CD не существует и следовательно по определению скрещивающихся прямых АВ скрещивается с CD.
Закрепление изученной теоремы (с устным обоснованием) (рис. 5).
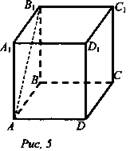
1. Определить взаимное расположение прямых АВ1 и DC. (АВ, скрещивается c DC.)
2. Указать взаимное расположение прямой DC и плоскости АА1ВВ1. (DC || плоскости АА1ВВ1.)
3. Является ли прямая АВ1 параллельной плоскостиDD1CC1? (Да.)
При обсуждении 2 и 3 задания обратить внимание на существование плоскости, проходящей через одну из скрещивающихся прямых и параллельной другой прямой.
Сформулировать теорему.
Теорема:
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.
Доказательство: учащиеся разбирают по учебнику самостоятельно с последующей записью на доске и в тетрадях.
Дано: АВ скрещивается CD (рис. 6).
Построить α: АВ ⊂ α, CD || α.
Доказать, что α - единственная.
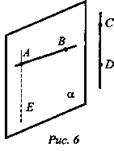
1. Через точку А проведем прямую АЕ, АЕ || CD.
2. Прямые АЕ и АВ пересекаются и образуют плоскость α. АВ ⊂ α (по построению), CD || α (по признаку параллельности прямой и плоскости), α - искомая плоскость.
3. Докажем, что α - единственная плоскость. α - единственная по следствию из аксиом. Любая другая плоскость, которой принадлежит АВ, пересекает АЕ и, следовательно, прямую CD.
Обратить внимание учащихся, что в доказательстве этой теоремы дается способ построения плоскости, проходящей через данную точку и параллельной двум скрещивающимся прямым. Рассмотреть задачу на построение.
Задача
Построить плоскость α, проходящей через точку К и параллельной скрещивающимся прямым а и b (рис. 7).
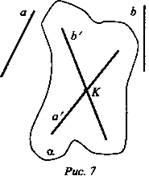
Построение:
1. Через точку К провести прямую а’ || а. (прямая а и точка К определяют плоскость; построение возможно и а’ - единственная прямая).
2. Через точку К провести прямую b’ || b.
3. Через пересекающиеся прямые проведем плоскость α. α - искомая, единственная плоскость.
IV. Закрепление изученного материала
1. Решение задач № 34 и 39 на доске и в тетрадях.
1) Задача № 34
Дано: D ∈ плоскости ABC. АМ = MD; DN = NB; DP = PC; К ∈ BN (рис. 8).
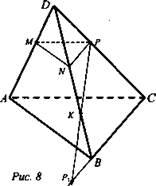
Определить взаимное расположение прямых:
а) ND и АВ. ND ∩ АВ = В (D, А, N и В лежат в одной плоскости и ![]() );
);
б) РК и ВС. РК ∩ ВС = P1 (К, Р, С, В лежат в одной плоскости и ![]() );
);
в) MN и АВ. MN || АВ (по свойству средней линии треугольника MN || АВ);
г) МР и АС. МР || АС (по свойству средней линии треугольника МР || АС);
д) KN и AC. KN ∩ плоскости ADC = D; D ∉ АС ⇒ KN скрещивается с АС по признаку скрещивающихся прямых;
е) MD и ВС; MD ∩ плоскости ABC = A, A ∉ ВС ⇒ MD скрещивается с ВС по признаку скрещивающихся прямых.
2) Задача № 39
Дано: АВ и CD скрещиваются (рис. 9).
Доказать, что AD и ВС скрещиваются.
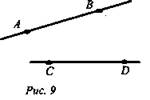
Доказательство:
1. Точка А, С, D лежат в одной плоскости (по аксиоме A1). Пусть эта плоскость α.
2. В g α, так как АВ и CD скрещиваются (по определению скрещивающихся прямых).
3. ВС ∩ α = С; С ∉ AD ⇒ AD и ВС скрещиваются (по признаку скрещивающихся прямых).
2. Самостоятельно решить задачи с последующей проверкой: № 93, 94.
1) Задача № 93
Дано: а || b. MN ∩ а = М (рис. 10).
Определить взаимное расположение прямых MN и b.
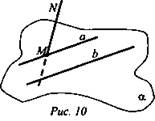
Решение:
1. a || b ⇒ существует плоскость α, проходящая через а и b.
2. ![]() MN и b скрещиваются (по признаку скрещивающихся прямых). (Ответ: MN и b скрещиваются.)
MN и b скрещиваются (по признаку скрещивающихся прямых). (Ответ: MN и b скрещиваются.)
2) Задача № 94
Дано: а скрещиваются Ь. В ∉ а и В ∉ b (рис. 11).
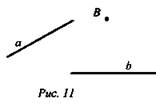
Определить взаимное расположение плоскостей α и β. α проходит через прямую а и точку В. β проходит через прямую b и точку В. α ∩ β, так как плоскости имеют одну общую точку и по аксиоме А3 они пересекаются и точка В принадлежит линии пересечения.
V. Подведение итогов
Домашнее задание
П. 7 № 35, 36, 37.
Дополнительная задача
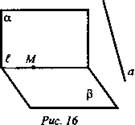
Плоскости α и β пересекаются по прямой l, которая является скрещивающейся с прямой а.
Докажите, что прямая а пересекает хотя бы одну из плоскостей α и β.
№ 35. Предположим, что а и b не скрещиваются ⇒ а || b или а ∩ b. Через а и b проведем плоскость β. Предположим, что а не скрещиваются с ⇒ а || с или а ∩ с. Через прямые а и с проведем плоскость γ. ![]() а - линия пересечения плоскостей β и γ.
а - линия пересечения плоскостей β и γ. ![]() что противоречит условию.
что противоречит условию.
Следовательно, а и b скрещиваются или а и с скрещиваются.
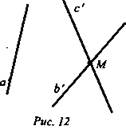
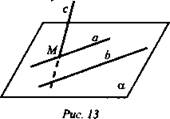
№ 36. а || b ⇒ существует плоскость α (рис. 13), которой принадлежат эти прямые, ![]() b и с скрещиваются по признаку скрещивающихся прямых.
b и с скрещиваются по признаку скрещивающихся прямых.
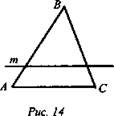
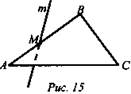
№ 37 (рис. 14, рис. 15).
а) Рис. 14. ![]() (по свойству параллельных прямых).
(по свойству параллельных прямых).
б) Рис. 15, m ∩ АВ = М, АВ ⊂ плоскости ABC ⇒ m ∩ плоскости ABC = М. ![]() m и ВС скрещиваются по признаку скрещивающихся прямых.
m и ВС скрещиваются по признаку скрещивающихся прямых.
Дополнительная задача
Пусть ![]() (рис. 16). Возьмем любую точку М на прямой l.
(рис. 16). Возьмем любую точку М на прямой l.
Через прямую а и М проведем плоскость γ.
![]() так как
так как ![]() (по А3).
(по А3).
![]() так как
так как ![]() (по А3).
(по А3).
![]()
Итак, ![]() чего быть не может, т. к.
чего быть не может, т. к. ![]() Следовательно, а ∩ α или а ∩ β.
Следовательно, а ∩ α или а ∩ β.