Поурочные разработки по геометрии 10 класс
Признак перпендикулярности прямой и плоскости - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) доказать признак перпендикулярности прямой и плоскости;
2) формировать навык применения признака перпендикулярности прямой й плоскости к решению задач.
Ход урока
I. Организационный момент
Сообщить тему урока и сформулировать цели.
II. Проверка домашнего задания
Проверка домашних задач по готовым чертежам. Три человека у доски готовят доказательство леммы и двух теорем. В это время класс работает устно по готовым чертежам.
1 . Дано: АВ ⊥ α, CD ⊥ α, АВ = CD (рис. 1).
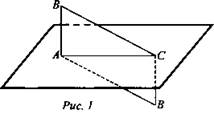
Определить вид четырехугольника ABCD (параллелограмм), так как по теореме п. 16 АВ || CD, а четырехугольник, у которого противолежащие стороны параллельны и равны, является параллелограммом.
2. Дано: ABCD - параллелограмм, АВ ⊥ α, АС = 8 (рис. 2).
Найти: BD.
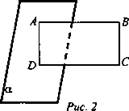
(BD = 8 см), так как АВ ⊥ α и АВ || DC, то CD ⊥ α. ABCD - прямоугольник ⇒ АС = BD и BD= 8.
3. Дано: ABCD - параллелограмм, BD ⊥ α, АВ = 6 (рис. 3).
Найти: РABCD.
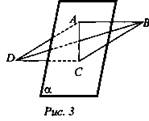
(ромб, Р = 24), так как BD ⊥ α ⇒ BD ⊥ АС ⇒ ABCD - ромб, Р = 4 · 6 = 24.
III. Изучение нового материал.
А) Актуализация знани.
Задача № 119 а)
Дано: ОА ⊥ α, ОА = OD (рис. 4).
Доказать: АВ = DB.
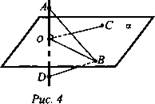
Доказательство: ОА ⊥ (ОВС) ⇒ ОА ⊥ ОВ по определению перпендикулярности прямой и плоскости. ВО - медиана и высота в ΔABD ⇒ ΔABD - равнобедренный ⇒ AB = DB.
Б) Верно ли утверждение:
«Прямая называется перпендикулярной плоскости, если она перпендикулярна какой-нибудь прямой, лежащей в этой плоскости». Ответ обоснуйте. (Нет, приводится контр. пример; рис. 5, 6, 7.)
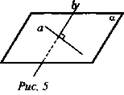
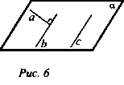
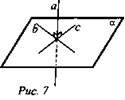
Возьмем две прямые. Две прямые на плоскости могут быть параллельными или пересекающимися (рис. 6, 7).
Что вы замечаете? Сформулируйте признак перпендикулярности прямой и плоскости. Признак формулируется. Записываются условия и требования.
План доказательства (на доске).
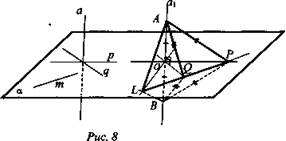
1 этап. Дано: ![]() (рис. 8).
(рис. 8).
Доказать: a ⊥ OL.
1) АО = ОВ.
2) AP = BP, AQ = BQ.
3) ΔAPQ = ΔBPQ, поэтому ∠APQ = ∠BPQ.
4) MPL = ABPL, поэтому AL = BL.
5) В ΔABL медиана LO является высотой, то есть АВ ⊥ OL или a ⊥ OL.
2 этап, m - произвольная прямая плоскости α, OL || m.
Так как a ⊥ OL, то а ⊥ m, и, следовательно, а ⊥ α.
3 этап. Дано: а ⊥ р, а ⊥ q.
Доказать: a ⊥ α.
1) а1 || а.
2) Так как a1 ⊥ α, то а ⊥ α.
IV. Закрепление изученного материала
Задача № 121
(Указание: медиана, проведенная в прямоугольном треугольнике к гипотенузе, равна ее половине) (рис. 9).
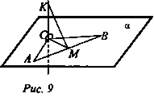
Решение: ![]()
![]() (теорема Пифагора), СМ = 5, КМ = 13 (теорема Пифагора).
(теорема Пифагора), СМ = 5, КМ = 13 (теорема Пифагора).
(Более сильные учащиеся решают задачу: Все грани параллелепипеда ABCDA1B1C1D1 - равные ромбы; углы между ребрами, имеющими общую точку А, равны. Выясните, перпендикулярна ли прямая А1С прямой B1D1).
Решение: Очевидно, что треугольники AA1D1 и АА1В1 равны, значит, АВ1 = AD1. Пусть О - середина отрезка B1D1. Значит, прямая B1D1 перпендикулярна плоскости АСС1, в которой лежат прямые А1О и АО. Прямая А1С также лежит в плоскости, поэтому прямые А1С и B1D1 перпендикулярны.
Дано: ABCD - параллелограмм, АМ = МС, ВМ = MD (рис. 10).
Доказать: МО ⊥ (ABC).
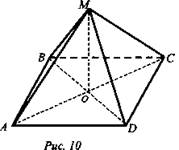
Доказательство:
1) ΔАМС - равнобедренный; МО - медиана =>МО ⊥ АС.
2) ΔBMD - равнобедренный; МО - медиана => МО ⊥ BD.
3) ![]()
![]()
V. Подведение итогов
Можно ли утверждать, что прямая, проходящая через центр круга, перпендикулярна:
а) диаметру (нет, по определению);
б) двум радиусам (нет, так как радиусы могут лежать на диаметре);
в) двум диаметрам (да, по определению).
Домашнее задание
1) п. 17.;
2) № 124, 126.
3) Дополнительная задача
В параллелепипеде МРКНМ1Р1К1Н1 все грани - ромбы; ∠М1МН + ∠М1МР = 180°. Выясните, перпендикулярна ли прямая Р1Н прямой МК.
(Ответ: да (задача решается аналогично задаче для сильных учащихся из классной работы..
Задача № 124
Дано: ![]()
![]() (рис. 11).
(рис. 11).
Доказать: PQ = P1Q1.
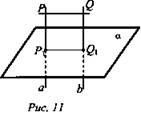
Доказательство:
![]()
Значит, PQQ1P1 - параллелограмм ⇒ PQ = P1Q1.
Задача № 126
Дано: ![]() (рис. 12).
(рис. 12).
Найти: вид ΔMBD.
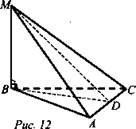
Решение:
![]()
Значит, AMBD - прямоугольный.