Поурочные разработки по геометрии 10 класс
Некоторые следствия из аксиом - АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ
Цель урока:
- ознакомить учащихся с данной темой, показать применение аксиом к решению задач.
Ход урока
I. Организационный момент
II. Проверка домашнего задания
Вопросы учащимся:
а) Решение задачи 3 (a) - учащиеся дают обоснованный ответ (да - первый случай аксиома А1, второй случай аксиома А2).
б) Сформулировать аксиомы планиметрии.
в) Сформулировать аксиомы A1-A3 стереометрии.
III. Новый материал
Докажем следствие из аксиом.
Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Учащиеся записывают формулировку теоремы - стр. 6 учебника.
Дано: а, М ∈ α.
Доказать: (а, М) ⊂ α.
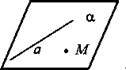
Доказательство: Отметим, что теорема содержит два утверждения: 1. О существовании плоскости. 2. О единственности плоскости.
а) Рассмотрим прямую а и не лежащую на ней точку М. Докажем, что через прямую а и точку М проходит плоскость. Отметим на прямой а 2 точки: P и Q. Точки М, Р и Q не лежат на одной прямой, поэтому согласно аксиоме A1 через эти точки проходит некоторая плоскость α. Так как 2 точки прямой а (Р и Q) лежат в плоскости α, то по аксиоме А2 плоскость α проходит через прямую а.
б) Единственность плоскости, проходящей через прямую А и точку М, следует из того, что любая плоскость, проходящая через прямую а и точку М, проходит через точки М, Р и Q. Следовательно, эта плоскость совпадет с плоскостью α, так как по аксиоме А1 через точки М, P и Q проходит только одна плоскость.
Теорема доказана.
Теорема 2. Через 2 пересекающиеся прямые проходит плоскость, и притом только одна.
Формулировку учащиеся записывают в тетрадь под руководством учителя с учебника (стр. 7).
Устно разбирают доказательство, а запись выполняют дома.
Учитель обращает внимание учащихся, что данная теорема также состоит их 2 утверждений: существования и единственности, и доказательство опирается не на аксиомы, а на следствие 1.
III. Закрепление изученного материала
Учащиеся работают в тетрадях.
Один учащийся выходит к доске и решает задачу 6, случай 1: точки лежат на одной прямой.
Дано: АВ, ВС, АС.
Доказать: (АВ, ВС, AC) ⊂ (ABC).
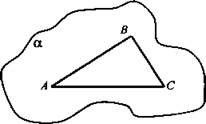
Доказательство: 1) (А, В, С) ∈ а, так как 3 точки принадлежат одной прямой, то по А2 (А, В, С) ∈ АВС;
2) (А, В, С) ∈ а. Через А, В и С по А1 проходит единственная плоскость. 2 точки каждого из отрезков АВ, АС и ВС лежат в плоскости, следовательно, по А2 прямые АВ, ВС, АС, а значит, и отрезки АВ, ВС, АС лежат в плоскости и т. д.
Задача с плаката
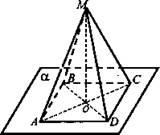
ABCD - ромб, О - точка пересечения его диагоналей, М - точка пространства, не лежащая в плоскости ромба. Точки A, D, О лежат в плоскости α.
Дайте ответ на поставленные вопросы с необходимыми обоснованиями.
1) Лежат ли в плоскости а точки В и С?
2) Лежит ли в плоскости МОВ точка D?
3) Назовите линию пересечения плоскостей МОВ и ADO.
4) Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60°. Предложите различные способы вычисления площади ромба. .
Учащиеся работают в тетради, предварительно сделав чертеж.
Дано: ABCD - ромб, AC ∩ BD = О, М ∈ α, (A, D, О) ∈ α. АВ = 4 см, ∠A = 60°.
Найти: (В, С) ∈ α, D ∈ MOB, MOB ∩ ADO, SABCD.
Решение: Учитель проводит фронтальную работу по вопросам плаката.
1) D ∈ α, О ∈ α, то по А2 DO ⊂ α, так как B ∈ DO, то В ∈ α.
Аналогично А ∈ α, О ∈ α, то по А2 АО ⊂ α, так как С ∈ AO, то С ∈ α.
2) OB ⊂ MOB, D ∈ OB, то D ∈ MOB.
3) О ∈ МОВ, О ∈ ADO.
В ∈ МОВ, В ∈ ADO ⇒ MOB ∩ ADO = ВО, но так как ВО - часть DB, то MOB ∩ ADO = DB.
Учитель обращает внимание учащихся на тот факт, что если 2 плоскости имеют общие точки, то они пересекаются по прямой, проходящей через эти точки.
4) ![]()
IV. Подведение итогов
Цель урока достигнута. Аксиомы стереометрии повторили, познакомили со следствиями и применили их при решении задач.
V. Оценки (с комментариями)
Домашнее задание
П. 2, 3, стр. 4-7.
Теорема 2, стр. 7 - записать доказательство.
Повторить А1-А3.
Задача .
Ответ:
а) нет, окружность можно вращать вокруг прямой, соединяющей эти две точки;
б) да.