Поурочные разработки по геометрии 10 класс
Решение задач на перпендикулярность прямой и плоскости - урок 2 - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) закрепить знания, умения и навыки учащихся по теме «Перпендикулярность прямой и плоскости»;
2) совершенствовать навыки решения задач.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация знаний учащихся
1. Проверка домашнего задания.
№ 129 - устно по заранее подготовленному чертежу;
№ 136 - решение подготовить на доске.
Дополнительную задачу проверить индивидуально у нескольких учеников.
Задача № 129
Дано: ABCD квадрат; AM - прямая; АМ ⊥ (ABCD); АС ∩ BD = О (рис. 1).
Доказать: a) BD ⊥ (АМО); б) МО ⊥ BD.
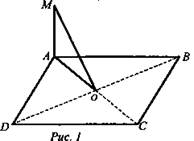
Доказательство:
1) Так как МА ⊥ (ABCD), то МА ⊥ BD (по определению прямой, перпендикулярной плоскости). BD ⊥ AC (по свойству диагоналей квадрата). МА ⊂ (МАО) и АС ⊂ (МАО), МА ∩ АС = А. Следовательно, BD ⊥ (MAO) (по признаку перпендикулярности прямой и плоскости).
2) Так как BD ⊥ (МАО), то BD ⊥ МО, МО ⊂ (МАО) (по определению прямой, перпендикулярной плоскости).
Задача № 136
Дано: АВ - отрезок; α; АВ ⊥ α; О - середина АВ, О ∈ α; ХА = ХВ. (рис. 2).
Доказать: X ∈ α.
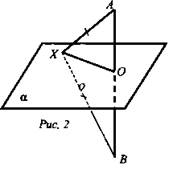
Доказательство:
1) Если X ∈ АВ, то Х = О, и поэтому X ∈ а.
2) Если X ∉ АВ, то ХО - медиана ΔАХВ. ΔАХВ - равнобедренный (по определению), значит, ХО - высота (по свойству медианы равнобедренного треугольника), то есть ХО ⊥ АВ. Таким образом, О ∈ ХО, О ∈ АВ и ХО ⊥ АВ, следовательно, ХО ⊂ а (по задаче № 134) и X ∈ а.
Дополнительная задача
Дано: ΔАВС; АВ = АС = ВС; CD ⊥ (ABC); AM = MB, DM = 15, CD = 12 (рис. 3).
Найти: SΔADB.
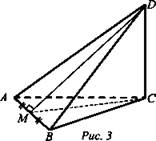
Решение:
1) CD ⊥ (ABC) ⇒ CD ⊥ AC и CD ⊥ ВС, тo есть ∠ACD = ∠BCD = 90° и ΔADC, ΔBDC -прямоугольные.
2) ΔADC = ΔBDC (по двум катетам): DC - общий, AC = ВС (по условию). Значит, AD = BD (как соответствующие в равных треугольниках), тогда ΔADB - равнобедренный (по определению) и DM - медиана. Следовательно, DM - высота (по свойству медианы равнобедренного треугольника).
3) DC ⊥ МС ⇒ ∠DCM = 90° и ΔMCD - прямоугольный. По теореме Пифагора: MD2 = DC2 + МС2. Тогда ![]()
4) ΔМСВ - прямоугольный (∠CMB = 90°, так как СМ - медиана и высота в ΔАВС - равностороннем), ![]() тогда
тогда 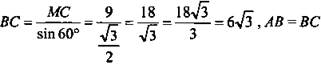 (по условию),
(по условию),
5) ![]() (Ответ: 45√3.)
(Ответ: 45√3.)
2. Решить самостоятельно задачу (выполняют учащиеся, у которых нет вопросов по домашнему заданию).
Дан тетраэдр МАВС, угольный, где D ∈ AC, MB ⊥ АВ. Найдите MD и SMBD, если MB = BD = а.
Дано: МАВС - тетраэдр; MB ⊥ АВ, MB ⊥ ВС; D ∈ AC, MB = BD = а (рис. 4).
Доказать: ΔMBD - прямоугольный.
Найти: MD; SMBD.
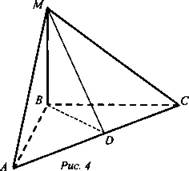
Решение: Так как ![]()
![]() то MB ⊥ (ABC) (по признаку перпендикулярности прямой и плоскости).
то MB ⊥ (ABC) (по признаку перпендикулярности прямой и плоскости).
Значит, ![]() (по определению прямой, перпендикулярной плоскости), то есть ∠MBD = 90°, а значит, ΔMBD - прямоугольный.
(по определению прямой, перпендикулярной плоскости), то есть ∠MBD = 90°, а значит, ΔMBD - прямоугольный.
2) ΔMBD, по теореме Пифагора: ![]()
![]()
3) ![]() (Ответ:
(Ответ: ![]() )
)
III. Математический диктант
I уровень
Ответы записать на листочек и в тетрадь.
Листочек сдается на проверку учителю, а тетрадь остается для самопроверки, которая будет проведена непосредственно по окончанию работы.
Вариант I |
Вариант II |
||||
1. Закончите предложение, чтобы получилось верное утверждение. Сделайте рисунок. |
|||||
1.1. Две прямые называются перпендикулярными, если... 1.2. Если плоскость перпендикулярна одной из двух параллельных прямых, то она... 1.3. Если две плоскости перпендикулярны прямой, то они... |
1.1. Прямая называется перпендикулярной к плоскости, если... 1.2. Две прямые, перпендикулярные одной и той же плоскости... 1.3. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая... |
||||
2. Ответьте на вопрос |
|||||
2.1. Сколько перпендикуляров можно провести через данную точку к данной прямой на плоскости? |
2.1. Сколько перпендикуляров можно провести через данную точку к данной прямой в пространстве? |
||||
3. Выпишите |
|||||
|
|||||
3.1. Ребра, перпендикулярные плоскости (DCC1). 3.2. Плоскости, перпендикулярные ребру ВВ1. |
3.1. Ребра, перпендикулярные плоскости (АВВ1). 3.2. Плоскости, перпендикулярные ребру A1D1. |
||||
4. Используя символы || и ⊥ запишите, как расположены прямая и плоскость (по рис. 5 из п. 3). Докажите. |
|||||
4.1. СС1 и DCB 4.2. D1C1 и DCB |
4.1. АА1 и DCB 4.2. В1С1 и DCB |
||||
5. АВ ⊥ α, CD ⊥ α, B ∈ α, D ∈ α, АВ = CD. Каково взаимное положение прямой АС и плоскости α? Ответ обоснуйте. |
5. AB ⊥ α, CD || АВ (В ∈ α, D ∈ α), Е ∈ α, ∠ECD = 40°. Тогда чему равны ∠CED? Ответ обоснуйте. |
||||
Ответы к заданиям математического диктанта
Вариант I |
Вариант II |
1.1. Угол между ними равен 90°. 1.2. Перпендикулярна и другой. 1.3. Параллельны. 2.1. Один. 3.1. AD, A1D1, ВС, В1С1. 3.2. АВС и А1В1С1. 4.1. СС1 ⊥ (DCB). 4.2. D1С1 || (DCB). 5. АС || α. |
1.1. Она перпендикулярна к любой прямой, лежащей в этой плоскости. 1.2. Параллельны. 1.3. Перпендикулярна плоскости. 2.1. Один. 3.1. AD1A1D1, BC1B1C1. 3.2. АА1В1 и DD1C1. 4.1. AA1 ⊥ (DCB). 4.2. B1C1 || (DCD). 5. ∠CED = 50°. |
II уровень
С самопроверкой по подготовленному решению задач.
№ 1. Основанием прямоугольного параллелепипеда является квадрат со стороной, равной а. Расстояние от бокового ребра до скрещивающейся с ним диагонали параллелепипеда равно... (рис. 6).
Найти: ρ (АА1; B1D).
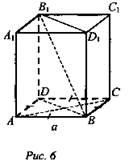
Решение:
1) ![]() (по признаку параллельности прямой и плоскости);
(по признаку параллельности прямой и плоскости); ![]()
2) Так как ABCD - квадрат, то AC ⊥ BD, то есть ![]()
3) ![]() (Ответ:
(Ответ: ![]() )
)
№ 2. ABCD - квадрат (рис. 7). АЕ - перпендикулярно плоскости квадрата, К ∈ BE. Чему равен угол между ВС и АК.
Найти: ∠(ВС; АК).
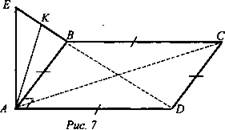
Решение:
1) Так как ВС и АК - скрещивающиеся прямые, то ∠(ВС, АК) = ∠(АК; AD), т. к. ВС || AD (по свойству сторон квадрата).
2) AE ⊥ AD (по определению прямой, перпендикулярной плоскости), АВ ⊥ AD, т. к. ∠BAD = 90°, АЕ ∩ АВ = А, значит, AD ⊥ (АВЕ) (по признаку перпендикулярности прямой и плоскости).
3) Так как AD ⊥ (АВЕ), то AD ⊥ АК, АК ⊂ (АВЕ) (по определению прямой, перпендикулярной плоскости). Значит, ∠ (АК, АВ) = ∠KAD = 90°.
(Ответ: 90°.)
IV. Решение задач
Задача 1
Отрезок АВ пересекает некоторую плоскость в точке О. Прямые AD и ВС, перпендикулярные этой плоскости, пересекает ее в точках D и С соответственно. AD = 6 см, ВС = 2 см, ОС = 1,5 см. Найдите АВ.
Дано: α; АВ - отрезок; ![]()
![]() (рис. 8).
(рис. 8).
Найти: АВ.
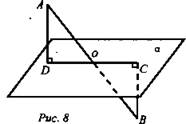
Решение:
1. Так как ![]()
2. Так как ![]() тo
тo
а) AD ⊥ DC и ВС ⊥ DC (по определению прямой, перпендикулярной плоскости). Значит, ∠ADC = ∠BCD = 90°;
б) AD || ВС (по теореме, обратной к теореме, о связи между параллельностью прямых и их перпендикулярностью к плоскости) и существует плоскость β: AD ⊂ β и ВС ⊂ β.
3. ΔADO и ΔВСО - прямоугольные, ∠ADC = ∠BCD = 90°. ∠A = ∠B (по свойству накрест лежащих углов, образованных параллельными прямыми AD и ВС и секущей АВ) ⇒ ΔADO ~ ΔВСО. Тогда ![]() (по определению подобных треугольников)
(по определению подобных треугольников) ![]()
![]()
4. В ΔADO, по теореме Пифагора: ![]() АО = 7,5 см. В ΔВСО, по теореме Пифагора: BO2 = ВС2 + СО2, ВO2 = 4 + 2,25. ВO = 2,5 см.
АО = 7,5 см. В ΔВСО, по теореме Пифагора: BO2 = ВС2 + СО2, ВO2 = 4 + 2,25. ВO = 2,5 см.
5. АВ = АО + ОВ, АВ = 7,5 + 2,5 = 10 (см). (Ответ: 10 см.)
Задачу у доски, решает один ученик. Остальные учащиеся записывают решение в тетрадь, исправляя и дополняя отвечающего (по необходимости).
Задача 2
Прямые АВ и CD перпендикулярны некоторой плоскости и пересекают ее в точках В и D соответственно. Найдите AС, если АВ = 9, CD = 15, BD = 8.
(Следует сообщить учащимся, что в задаче возможны два варианта расположения точек А, С и плоскости.)
а) точки А и С лежат по одну сторону от плоскости (у доски работает один ученик, выполняет полное решение со всеми необходимыми обоснованиями);
б) точки А и С лежат по разные стороны от плоскости (у доски работает один ученик, самостоятельно выполняя решение. Можно составить только план решения).
а) Дано: ![]()
![]() (рис. 9).
(рис. 9).
Найти: AC.
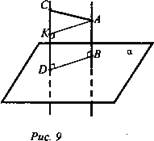
Решение:
1. ![]()
2. Так как ![]() то АВ ⊥ BD и CD ⊥ BD (по определению прямой, перпендикулярной плоскости).
то АВ ⊥ BD и CD ⊥ BD (по определению прямой, перпендикулярной плоскости).
3. Так как АВ ⊥ α и CD ⊥ α, то АВ || CD (по теореме, обратной к теореме о связи между параллельностью прямых и их перпендикулярностью к плоскости) и существует плоскость β: АВ ⊂ β и CD ⊂ β. Тогда ABCD - трапеция, прямоугольная. Пусть АК - высота трапеции, тогда АК ⊥ KD. ABDK - прямоугольник (по признаку - углы прямые); АВ = KD = 9, BD = АК = 8 (по свойству сторон прямоугольника).
4. ΔАКС - прямоугольный: КС = CD - KD, КС = 15 - 9 = 6. По теореме Пифагора: ![]() (Ответ: 10..
(Ответ: 10..
б) Рис. 9 а
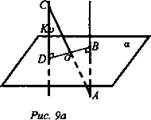
Решение:
1-2 аналогично случаю а.
3. ![]() Так как ВО + OD = 8, то ВО = 3, DO = 5.
Так как ВО + OD = 8, то ВО = 3, DO = 5.
![]()
![]() (Ответ: 8√10.)
(Ответ: 8√10.)
Задача № 3
Диагональ BD параллелограмма ABCD перпендикулярна плоскости α. Найдите периметр параллелограмма, если АВ = 7 см, точки А и С лежат в плоскости α.
Дано: α; ABCD - параллелограмм; ![]()
![]() (рис. 10).
(рис. 10).
Найти: РABCD.
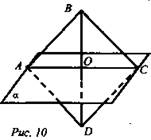
Решение:
1) Так как А ∈ α, С ∈ α, то ![]() (по определению прямой, перпендикулярной плоскости). Значит, ABCD - ромб (по признаку). Тогда АВ = ВС = CD = AD = 7 см (по определению ромба).
(по определению прямой, перпендикулярной плоскости). Значит, ABCD - ромб (по признаку). Тогда АВ = ВС = CD = AD = 7 см (по определению ромба).
2) РABCD = 4 · 7 = 28 (см). (Ответ: 28 см.)
V. Подведение итогов
Домашнее задание
1) Повторить теоретический материал по изученной теме.
2) Решить задачи № 131, дополнительные задачи:
1. Отрезок МН пересекает некоторую плоскость в точке К. Через концы отрезка проведены прямые HP и ME, перпендикулярные плоскости и пересекающие ее в точках Р и Е. Найдите РЕ, если HP = 4 см, НК = 5 см, ME = 12 см.
2. Треугольник ABC правильный, точка О - его центр. Прямая ОМ перпендикулярна плоскости ЛВС. Докажите, что МА = MB = МС. Найдите МА, если АВ = 6 см, МО = 2 см.
3. ABCD прямоугольник. Отрезок АЕ перпендикулярен к плоскости ABC. ЕВ = 15, ЕС = 24, ED = 20. Докажите, что треугольник EDC прямоугольный, и найдите АЕ.
4. Точка А принадлежит окружности, АК - перпендикуляр к ее плоскости, АК = 1 см, АВ - диаметр, ВС — хорда окружности, составляющая с АВ угол 45°. Радиус окружности равен 2 см. Докажите, что треугольник КСВ прямоугольный, и найдите КС.
I уровень - № 131, дополнительные задачи № 1, 2.
II уровень - № 131, дополнительные задачи № 3, 4.
Решение задач домашнего задания.
Задача № 131
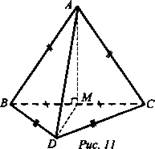
Дано: ABCD - тетраэдр; М ∈ ВС: ВМ = МС; АВ = AC, DB = DC (рис. 11).
Доказать: (ADM) ⊥ DC.
Доказательство:
1. Так как АВ = АС, то ΔАВС - равнобедренный (по определению) и AM - медиана. Тогда AM - высота ΔАВС (по свойству медианы равнобедренного треугольника). Значит, AM ⊥ ВС.
2. Так как DB = DC, то ΔBCD - равнобедренный и DM - медиана. Тогда DM - высота, а значит, DM ⊥ ВС.
3. 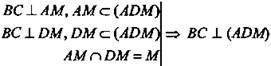 или (ADM) ⊥ ВС (по признаку перпендикулярности прямой и плоскости).
или (ADM) ⊥ ВС (по признаку перпендикулярности прямой и плоскости).
Задача № 1
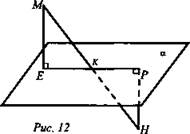
Дано: α, МН - отрезок, ![]()
![]() НР = 4 см, НК = 5 см, ME = 12 см (рис. 12).
НР = 4 см, НК = 5 см, ME = 12 см (рис. 12).
Найдите: РЕ.
Решение:
1) ![]()
2) ![]() (по определению прямой, перпендикулярной плоскости) и ME || ЯР (по теореме, обратной к теореме, о связи между параллельностью прямых и их перпендикулярностью к плоскости), тогда существует плоскость β: ME ⊂ β.
(по определению прямой, перпендикулярной плоскости) и ME || ЯР (по теореме, обратной к теореме, о связи между параллельностью прямых и их перпендикулярностью к плоскости), тогда существует плоскость β: ME ⊂ β.
3) Так как ME ⊥ РЕ и HР ⊥ РЕ, то ∠МЕК = ∠HPK = 90°, а ΔМЕК и ΔНРК - прямоугольные.
4) ΔНРК; НК2 = HР2 + КР2 (по теореме Пифагора). КР2 = НК2 - HP2, ![]()
5) ∠EMK = ∠PHK (по свойству накрест лежащих углов, образованных параллельными прямыми ME и HР и секущей МН). Тогда ΔМЕК ~ ΔНРК и ![]() (по определению подобных треугольников);
(по определению подобных треугольников); ![]()
6) РЕ = РК + КЕ, РЕ = 3 + 9 = 12 (см). (Ответ: 12 см..
Задача № 2
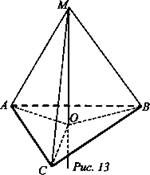
Дано: ΔАВС, АВ = ВС = АС; О - центр ΔАВС; ОМ ⊥ (ABC); АВ = 6 см, МО = 2 см (рис. 13).
Доказать: МА = MB = МС.
Найти: МА.
Решение:
1) Так как О - центр ΔАВС, то АО = ВО = СО = R.
2) Так как МО ⊥ (ABC), то МО ⊥ АО, МО ⊥ ВО, МО ⊥ СО (по определению прямой, перпендикулярной плоскости). Тогда ∠MOA = ∠MOB = ∠MOC = 90°, а ΔМАО, ΔМВО и ΔМСО - прямоугольные.
3) ΔМАО = ΔМВО = ΔМСО (по двум катетам): МО - общий, АО = ВО = СО. Следовательно, МА = MB = МС.
4) ![]() По теореме Пифагора:
По теореме Пифагора: ![]() (Ответ: 4 см.)
(Ответ: 4 см.)
Задача № 3
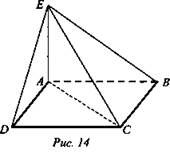
Дано: ABCD - прямоугольник; АЕ ⊥ (ABC); ЕВ = 15, ЕС = 24, ED = 20 (рис. 14).
Доказать: ΔEDC - прямоугольный.
Найти: АЕ.
Решение:
1) Так как АЕ ⊥ (АВС), то AE ⊥ AD ![]()
![]() (по определению прямой, перпендикулярной плоскости). Значит, ∠DAE = ∠CAE = ∠BAE = 90°, a ΔDAE, ΔCAE, ΔBAE - прямоугольные.
(по определению прямой, перпендикулярной плоскости). Значит, ∠DAE = ∠CAE = ∠BAE = 90°, a ΔDAE, ΔCAE, ΔBAE - прямоугольные.
2) ΔDAC - прямоугольный, ∠D = 90°, так как ABCD - прямоугольник. По теореме Пифагора: ![]() (DC = АВ - по свойству сторон прямоугольника).
(DC = АВ - по свойству сторон прямоугольника).
3) По теореме Пифагора в ΔDAE: ![]() в ΔСАЕ:
в ΔСАЕ: ![]() в ΔВАЕ:
в ΔВАЕ: ![]()
![]() подставим (1) и (3) в (2), получим.
подставим (1) и (3) в (2), получим.
![]()
![]()
![]()
4) 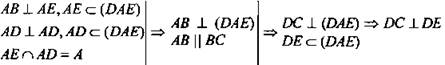 Значит, ∠CDE = 90° и ΔEDC - прямоугольный.
Значит, ∠CDE = 90° и ΔEDC - прямоугольный.