Поурочные разработки по геометрии 10 класс
Повторение теории. Решение задач на применение теоремы о трех перпендикулярах (ТПП), на угол между прямой и плоскостью - ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) повторить доказательство теоремы о трех перпендикулярах, понятия угла между прямой и плоскостью;
2) закрепить навыки решения задач.
Ход урока
I. Проверка домашнего задания
1. 1 человек доказывает ТПП, 1 человек на доске решает одну из домашних задач.
2. Работа с классом устно.
- Что называется перпендикуляром и наклонной?
Проведем через точку А прямую, перпендикулярную α, а ∩ α = Н (рис. 1).
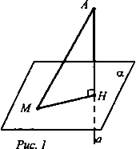
Отрезок АН называется перпендикуляром, точка Н - основание. Возьмем любую точку М ∈ α и отличную от Н. Отрезок AM называется наклонной. Отрезок НМ - проекция наклонной.
Длина перпендикуляра всегда меньше длины любой наклонной, проведенной из той же точки к этой плоскости. Длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости α.
- Что называется расстоянием между параллельными плоскостями? Привести примеры (расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости).
- Что называется расстоянием между прямой и параллельной ей плоскостью? Привести примеры (расстояние от произвольной точки прямой до плоскости).
- Что называется расстоянием между скрещивающимися прямыми? Привести примеры (расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую, параллельную первой).
II. Решение зада.
Задача № 1
В ΔАВС АВ = ВС = 10 см, АС = 12 см.
Через точку В к плоскости треугольника проведен перпендикуляр BD длиной 15 см.
а) Укажите проекцию ΔDBC на плоскость ABC.
б) Найдите расстояние от точки D до прямой АС.
Дано: ΔАВС, АВ = ВС = 10 см, АС = 12 см, DB ⊥ (ABC), DB = 15 см (рис. 2).
Найти: а) проекцию ΔDBC на (ABC), б) расстояние от точки D до АС.
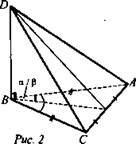
Решение:
а) 1. Так как DB ⊥ (ABC) по условию, то проекцией отрезка DB является точка В, проекцией наклонной DC является отрезок ВС.
2. Проекцией ΔDBC на (ABC) является отрезок ВС.
б) 1. Расстояние от точки D до прямой АС-это длина перпендикуляра.
2. Так как в ΔDBC ∠B = 90° и в ΔDBA ∠B = 90°, катет DB общий, ВА = ВС по условию, то ΔDBC = ΔDBA по двум катетам. Значит, DA = DC.
Вывод: Если проекции наклонных равны, то и сами наклонные равны и наоборот.
3. ΔCDA - равнобедренный.
4. DK - высота, медиана и биссектриса в ΔCDA. Значит, длина отрезка DK - это расстояние от точки D до АС.
5. ΔDBK, ∠B = 90°, ![]()
6. Что мы знаем о ΔABC? (Он равнобедренный, и мы знаем длины его сторон.) Применим теорему косинусов, ![]()
![]()
7. ВК является катетом в одном из равных треугольников ВКА и ВКС. Рассмотрим ΔВКА, ∠K = 90°, ![]()
![]()
![]() Так как в ΔАКB, ∠K = 90°, ∠B - острый, то cos ∠B > 0. Значит,
Так как в ΔАКB, ∠K = 90°, ∠B - острый, то cos ∠B > 0. Значит, ![]()
8. ![]() (Ответ: а) BС; б) 17 см.)
(Ответ: а) BС; б) 17 см.)
III. Подведение итогов
- Какие теоретические вопросы по теме мы использовали при решении этой задачи?
Домашнее задание
§ 2, № 147, 151.
№ 147. Дано: ABCD - прямоугольник, MB ⊥ (ABCD) (рис. 3).
Доказать: ΔAMD и ΔMCD - прямоугольные.
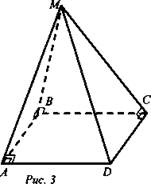
Доказательство:
1. MB - перпендикуляр, AM и МС - наклонная, АВ и ВС их проекции.
2. Так как AD ⊥ АВ, по ТТП AD ⊥ AM, в ΔAMD ZA = 90°.
3. Так как DC ⊥ ВС, то по ТТП CD ⊥ МС, в ΔDCM ZC = 90°.
№ 151. Дано: ΔАВС, CD ⊥ (АВС), СН - высота ΔABC.
Доказать: a) ΔABC - проекция ΔABD на (ABC); б) DH - высота ΔABD.
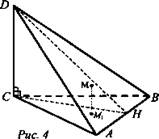
Доказательство:
a) CD - перпендикуляр к (АВС), С - проекция точки D. Отрезок СВ - проекция наклонной DB, а СА - проекция DA на (АВС), АВ ⊂ (ABС).
Проекциями сторон ΔАВС на (ABC) являются соответствующие стороны ΔАВС. Если М любая внутренняя точка ΔABD, то M1 ее проекция тоже является внутренней точкой ΔАВС. Таким образом, ΔАВС является проекцией ΔABD на (ABC).
б) АВ ⊥ СН по условию, АВ ⊥ DH по ТПП, то есть DH - высота ΔABD.