Поурочные разработки по геометрии 10 класс
Решение задач на свойства прямоугольного параллелепипеда - ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) повторить свойства прямоугольного параллелепипеда;
2) решить часть задач на свойства прямоугольного параллелепипеда.
Ход урока
I. Актуализация знаний
1) Один ученик у доски доказывает свойства прямоугольного параллелепипеда, другой теорему о диагонали прямоугольного параллелепипеда.
2) Устный счет:
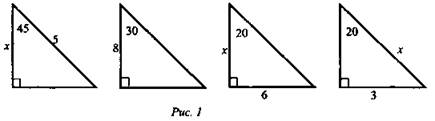
3) Формирование навыков и умений у учащихся.
№ 195. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; АС1 = 12 см; D1; AA1D1 = 30°; ∠BD1D = 45° (рис. 2).
Найти: АВ, AD, АА1.
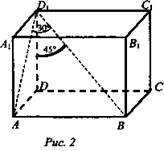
Решение:
1) BD1 = AC1 = 12 см;
2) АВ ⊥ ADD1, значит, AD1 - проекция BD1 на плоскость AA1D1, значит, ∠AD1B = 30°;
3) Из ΔABD1: ![]()
4) ΔDD1B - прямоугольный равнобедренный; ∠D1DB = 90°, так как ∠DD1B = 45° ⇒ DD1 = DB = х, по теореме Пифагора ![]()
![]() то есть
то есть ![]() Из прямоугольного треугольника АОВ найдем AD по теореме Пифагора (∠DAB = 90°),
Из прямоугольного треугольника АОВ найдем AD по теореме Пифагора (∠DAB = 90°), ![]()
![]() (Ответ: 6 см, 6 см, 6√2 см.)
(Ответ: 6 см, 6 см, 6√2 см.)
№ 1966. Дано: ABCDA1B1C1D1 - куб (рис. 3).
Построить: сечение плоскостью, проходящей через АВ и ⊥ CDА.
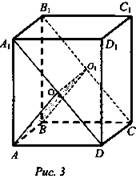
Построение: проведем АО ⊥ A1D, так как AA1D1D - квадрат ![]() Соединим ОО1; АВО1О - искомое сечение.
Соединим ОО1; АВО1О - искомое сечение.
Вопросы: Какой фигурой является АВО1О? Ответ объясните. Найдите его площадь, если ребро куба а.
Решение: ![]()
Самостоятельная работа
I уровень
1) Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; АВ = 6 см, AD = 4 см, АА1 = 12 см (рис. 4).
Найти: АС1.
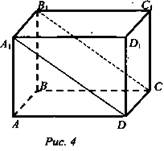
Решение: ![]()
![]() (Ответ: 14 м.)
(Ответ: 14 м.)
2) Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; АВ = 4 м, AD = 3, ![]()
Найти: Sбок..
Решение: ![]() по теореме Пифагора
по теореме Пифагора ![]()
![]()
![]() (Ответ: 56 см2.)
(Ответ: 56 см2.)
II уровень
Дан прямоугольный параллелепипед. Угол между диагональю основания и одной из его сторон равен β. Найдите площадь боковой поверхности параллелепипеда, если диагональ основания равна k.
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, ∠BDC = α, ∠B1DC = β; диагональ BD = k (рис. 5).
Найти: Sбок..
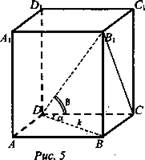
Решение: Рассмотрим прямоугольный ΔBDC: ![]()
![]() так как
так как ![]()
Из прямоугольного ΔB1CD: ![]()
![]()
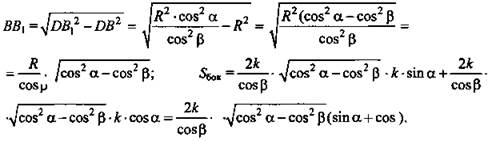
III уровень
Диагональ прямоугольного параллелепипеда образует с меньшей гранью угол β. Через большие стороны верхнего и нижнего основания проведено сечение, образующее с плоскостью основания угол. Зная, что периметр равен Р, найдите измерения параллелепипеда.
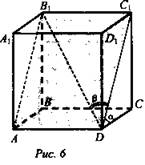
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; ∠A1DC1 = β; AB1C1D - сечение параллелепипеда; ![]() (рис. 6).
(рис. 6).
Найти: AD, АВ, АА1.
Решение: ![]() LB1C1D = 90° по теореме о 3-х перпендикуляpax;
LB1C1D = 90° по теореме о 3-х перпендикуляpax; ![]() подставить в (1), получим
подставить в (1), получим ![]() вынесем
вынесем
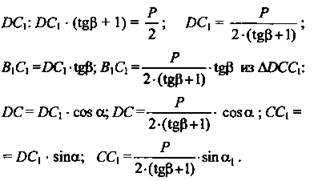
(Ответ: ![]()
![]() )
)
V. Подведение итогов
Домашнее задание
А - № 192, 194, 196 a.
В - 1) Стороны основания и диагональ прямоугольного параллелепипеда равны 8 дм, 9 дм. Чему равна площадь диагонального сечения?
2) Диагонали трех граней прямоугольного параллелепипеда, сходящихся в одной вершине, равны 8 м, 10 м и 12 м. Найдите линейные размеры этого параллелепипеда.