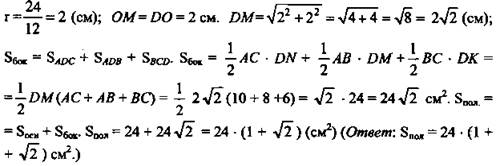Решение задач по теме «Пирамида». Самостоятельная работа - ПИРАМИДА - МНОГОГРАННИКИ

Цели урока:

1) закрепить навыки решения задач о пирамидах;

2) провести самостоятельную работу на вычисление элементов и площади поверхности правильной пирамиды.

Ход урока

I. Организационный момент

Собрать тетради с домашней работой для проверки.

II. Самостоятельная работа (контролирующая)

Вариант I

1 задача

Высота правильной треугольной пирамиды равна а√3 ; радиус окружности, описанной около ее основания, 2а. Найдите: а) апофему пирамиды; б) угол между боковой гранью и основанием; в) площадь боковой поверхности; г) плоский угол при вершине пирамиды.

I уровень

Основание пирамиды - прямоугольник со сторонами 6 и 8 см. Высота пирамиды равна 12 см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды.

II уровень

В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковой грани к плоскости основания равен 60°. Найдите боковое ребро пирамиды.

III уровень

Основанием пирамиды является треугольник со сторонами 12 см, 10 см, 10 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь полной поверхности пирамиды.

Вариант II

1 задача

Апофема правильной четырехугольной пирамиды равна 2а. Высота пирамиды равна а√3. Найдите: а)° сторону основания пирамиды; б)° угол между боковой гранью и основанием; в)° площадь поверхности пирамиды; г) расстояние от центра основания пирамиды до плоскости боковой грани.

I уровень

Основание пирамиды - ромб с диагоналями 10 и 18 см. Высота пирамиды проходит через точку пересечения диагоналей ромба. Меньшее боковое ребро пирамиды равно 13 см. Найдите большее боковое ребро пирамиды.

II уровень

Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенуза АВ равна 29 см, катет АС равен 21 см. Ребро DA перпендикулярно к плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.

III уровень

Основанием пирамиды является треугольник со сторонами 10 см, 8 см, 6 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь полной поверхности пирамиды.

III. Подведение итогов

Дома: поменяться вариантами.

Вариант I

1 задача

1. Ответ:

I уровень

Дано: SABCD - пирамида; ABCD — прямоугольник; SO = 12 (см); АВ = 6 (см); ВС = 8 (см) (рис. 1).

Найти: SD.

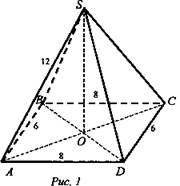
Решение: Пусть SABCD - данная пирамида, SO ⊥ ABCD. ΔABD - прямоугольный. По теореме Пифагора получим: ВО = OD = 5 (см); ΔSOD – прямоугольный треугольник. (Ответ: SD = 13 см.)

II уровень

Дано: SABCD - пирамида; АВ = DC = СВ = АВ = 6 см; ∠SKO = 60° (рис. 2).

Найти: SA.

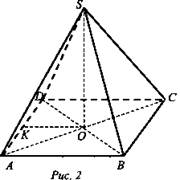
Решение: Пусть SABCD - данная пирамида; Из ΔOKS (прямоугольный) имеем: АК = 1/2DA = 3 (см). Из ΔAKS по теореме Пифагора имеем: Так как в правильной пирамиде все боковые ребра равны, то SA = SB = SC = SD = 3√5 (см). (Ответ: 3√5 см.)

III уровень

Дано: DABC - пирамида; АС = 12 (см); СВ = 10 (см); АВ = 10 (см); ∠DMO = 45°; ∠DMO = ∠DKO = ∠DNO (рис. 3).

Найти: Snол..

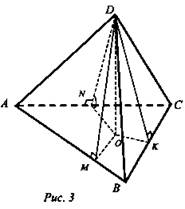
Решение: Пусть DABC - данная пирамида. DO - высота. Построим ОМ ⊥ АВ, ON ⊥ АС, ОК ⊥ ВС. Из теоремы о 3-х перпендикулярах следует, что DM ⊥ АВ, DK ⊥ BC, DN ⊥ AC. Пусть ∠DMO, ∠DKO, ∠DNO - линейные углы двугранных углов боковых граней с плоскостью основания. По условию ∠DMO = ∠DKO = ∠DNO = 45°. Тогда ΔDMO = ΔDKO = ΔDNO по катету и острому углу, из равенства треугольников следует: МО = OK = ON = r, DM = DK = DN: r - радиус вписанной в ΔАВС окружности, ОМ = DO, так как ΔMOD - равнобедренный.

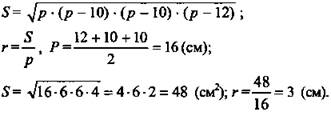То есть OM = DO = 3 см,

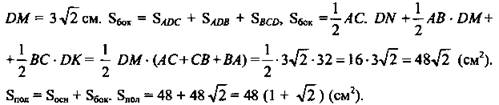
(Ответ: )

Вариант II

1 задача

(Ответ: г) а.)

I уровень

Дано: SABCD - пирамида; ABCD - ромб; АС = 18 (см); BD = 10 (см); SO ⊥ ABCD; SD = 13 (см) (рис. 4).

Найти: SC.

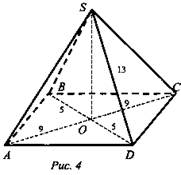
Решение: Пусть SABCD - данная пирамида. По теореме Пифагора, ΔSOD, ΔSOC - прямоугольные треугольники. (Ответ: SC = 15 см.)

II уровен.

Дано: ABCD - пирамида; АВ = 29 (см); АС = 21 (см); DA ⊥ AВС; DA = 20 (см) (рис. 5).

Найти: S6ок..

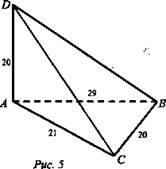
Пусть DABC - данная пирамида. Так как DA ⊥ ВС, АС ⊥ ВС, то по теореме о 3-х перпендикулярах DC ⊥ СВ. По теореме Пифагора имеем: DC .

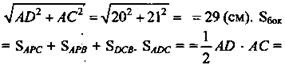
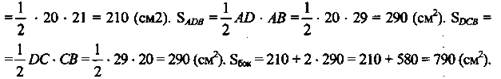
(Ответ: S6ок. = 790 см 2.)

III уровень

Дано: DABC - пирамида, AC = 10 (см); AB = 8 (см); BC = 6 (см). ∠DMO = 45° (рис. 6)

Найти: Snол..

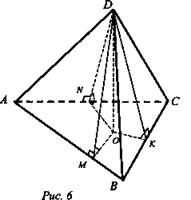
Решение: Пусть DABC - данная пирамида. DO - высота. Построим ОМ ⊥ АВ, ON ⊥ AC, OK ⊥ ВС. Из теоремы о 3-х перпендикулярах следует, что DM ⊥ АВ, DK ⊥ ВС, DN ⊥ AC. Пусть ∠DMO, ∠DKO, ∠DNO - линейные углы двугранных углов боковых граней с плоскостью основания. По условию ∠DMO = ∠DKO = ∠DNO = 45°. Тогда ΔDMO = ΔDKO = ΔDNO по катету и острому углу, из равенства треугольников следует: MO = OK = ON = r, DM = DK = DN; r - радиус вписанной в ΔАВС окружности, ОМ = DO, так как ΔMOD - равнобедренный.