Зачет № 3 по теме «Многогранники. Площадь поверхности призмы, пирамиды» - ПРАВИЛЬНЫЕ МНОГОГРАННИКИ - МНОГОГРАННИКИ

Цели урока:

1) проверить уровень теоретических знаний;

2) умение решать задачи и навыки учащихся по теме «Многогранники».

I уровень

Карточка № 1

1. Призма. Площадь боковой поверхности прямой призмы.

2. Основания прямой призмы - ромб со стороной 5 см и тупым углом 120°. Боковая поверхность призмы имеет площадь 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.

3. Сторона правильной треугольной пирамиды равна 6 см, а высота √13 см. Найдите площадь боковой поверхности пирамиды.

Карточка № 2

1. Пирамида. Площадь боковой поверхности правильной пирамиды.

2. Основание прямой призмы - ромб с острым углом 60°. Боковое ребро призмы равно 10 см, а площадь боковой поверхности - 240 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.

3. Боковое ребро правильной треугольной пирамиды равно 5 см, а высота √13 см. Найдите площадь боковой поверхности пирамиды.

II уровень

Карточка № 1

1. Правильные многогранники.

2. Основание прямого параллелепипеда - ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений Р и Q.

3. Основание пирамиды - прямоугольный треугольник с катетом 4√3 см и противолежащим углом 60°. Все боковые ребра пирамиды наклонены к плоскости основания под углом 45°. Найдите площадь боковой поверхности пирамиды.

Карточка № 2

1. Площадь боковой поверхности правильной усеченной пирамиды.

2. Диагональное сечение правильной четырехугольной призмы имеет площадь Q. Найдите площадь боковой поверхности призмы.

3. Основание пирамиды - прямоугольный треугольник с острым углом 30°. Высота пирамиды равна 4 см и образует со всеми боковыми ребрами углы 45°. Найдите площадь боковой поверхности пирамиды.

III уровень

Карточка № 1

1. Призма. Площадь боковой поверхности прямой призмы.

2. В прямой призме АВСА1В1С1 АВ = 13, ВС = 21, АС = 20. Диагональ боковой грани А1С составляет с плоскостью грани СС1В1В угол 30°. Найдите площадь полной поверхности призмы.

3. В правильной четырехугольной пирамиде сторона основания равна а, угол между смежными боковыми гранями равен 120°. Найдите площадь боковой поверхности пирамиды.

Карточка № 2

1. Пирамида. Площадь боковой поверхности правильной пирамиды.

2. В прямом параллелепипеде ABCDA1B1C1D1 AD = 17, DC = 28, АС = 39. Диагональ боковой грани A1D составляет с плоскостью боковой грани DD1C1C угол 45°. Найдите площадь полной поверхности параллелепипеда.

3. В правильной треугольной пирамиде сторона основания равна m. Угол между смежными боковыми гранями равен 120°. Найдите площадь боковой поверхности пирамиды.

Решения

I уровень (карточка 1)

№ 1. Дано: ABCDA1B1C1D1 - прямая призма. ABCD - ромб. AD = 5 см; ∠B = 120°; S6ок. = 240 см2.

Найти: Sсеч.

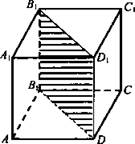
Решение: Сечение, проходящее через боковое ребро и меньшую диагональ основания BB1D1D. BB1D1D - прямоугольник. Sсеч. = BD · DD1. AA = 180° - 120° = 60°, так как ABDC - ромб, то ΔABD - равносторонний и BD = AD = 5 см. (Ответ: 60 см2.)

№ 2. Дано: DABC - правильная треугольная пирамида АВ = ВС = АС = 6 см. DO - высота; DO = √3.

Найти: Sбок.

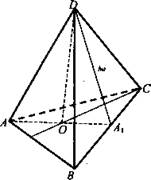
Решение: Так как пирамида правильная, то О - центр описанной и вписанной в ΔАВС окружности. где ha - апофема боковой грани. Росн. = 3 · 6 = 18 см. Рассмотрим ΔАА1С: (Ответ: Sбок. = 36 см2.)

I уровень (карточка 2)

№ 1. Дано: ABCDA1B1C1D1 - прямая призма. ABCD - ромб. ∠A = 60°. AA1 = 10 см. Sбок. = 240 см2.

Найти: Sсеч.

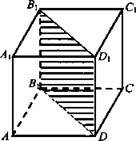
Решение: Сечение, проходящее через боковое ребро и меньшую диагональ основания BB1D1D. BB1D1D - прямоугольник. Sсеч. = BD · DD1. AB = DC = АС (по условию). АВ = 24/4 = 6 см. Рассмотрим ΔABD, так как ∠А = 60°, то ΔABD - равносторонний. BD = 6 см. Sсеч = 6 · 10 = 60 см. (Ответ: 60 см.)

№ 2. Дано: DABC - правильная треугольная пирамида DC = DB = AD = 5 см. DO - высота; DO = √13 cm.

Найти: Sбок.

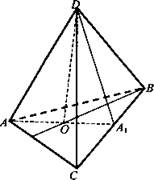
Решение: где ha – апофема боковой грани. Рассмотрим ΔAOD: Итак, hа = 4 (см). Рассмотрим ΔАВС - равносторонний. (Ответ: Sбок. = 36 см2.)

II уровень (карточка 1)

№ 1. Дано: ABCDA1B1C1D1 - прямой параллелепипед. ABCD - ромб. SAC1CA = Р; SB1D1DB = Q.

Найти: Sбок.

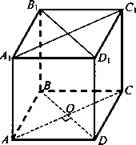
Решение:

1)

2)

3) Диагонали ромба, пересекаясь, делятся пополам и взаимно перпендикулярны.

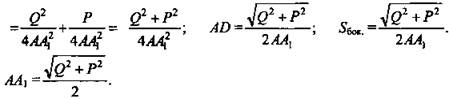
(Ответ: )

№ 2. Дано: DABC - пирамида ∠C = 90°; СА = 4√3 (см); ∠B = 60°; ∠DBO = ∠DAO = ∠DCO = 45°.

Найти: Sбок.

Решение: Так как ребра пирамиды наклонены под одним и тем же углом, то ОА = ОВ = СО. Точка О - центр описанной около ΔАВС окружности и является серединой гипотенузы.

1) Рассмотрим ΔADB: ΔDAO – равнобедренный (∠DAO = 45°). Следовательно, AO = DO. АО = 1/2AВ. АВ определим из ΔABC.

2) Рассмотрим ΔCDA: DM определим из ΔDOM. ОМ определим из ΔАВС. ОМ = 1/2BС. ВС = 1/2АВ (катет против угла в 30°). ВС = 4 см. МО = 2 см.

3) Рассмотрим ΔCDB:

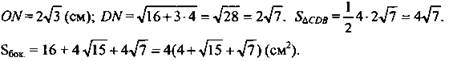
(Ответ: )

II уровень (карточка 2)

№ 1. Дано: ABCDA1B1C1D1 - правильная четырехугольная призма. ABCD - квадрат. SACA1C1 =Q.

Найти: Sбок.

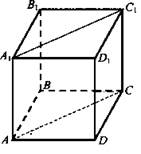
Решение: Рассмотрим ΔADC: AC2 = AD2 + DC2, так как ABCD - квадрат, то AC2 = 2AD2.

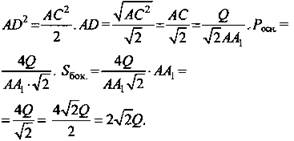
(Ответ: )

№ 2. Дано; DABC - пирамида. ΔАВС - прямоугольный; ∠С = 90°; ∠В = 30°; DO - высота; DO = 4 см. ∠ADO = ∠BDO = ∠CD.

Найти: Sбок.

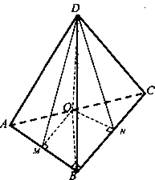
Решение: ΔADO = ΔDBO = ΔCDO (по катету и острому углу). Следовательно, АО = ОB = ОС. Значит, точка О - центр описанной около ΔАВС окружности и, следовательно, - середина гипотенузы. Из равенства треугольников следует АО = ОВ = ОС = OD (равнобедренные, прямоугольные). АО = 4 см. АВ = 8 см. Рассмотрим ΔАВС:

1. Рассмотрим ΔADB:

2. Рассмотрим ΔADC:

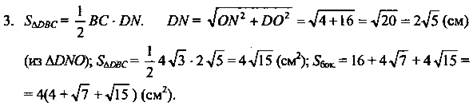
(Ответ: )

III уровень (карточка 1)

№ 1. Дано: ABCA1B1C1 - прямая призма. AB = 13, BС = 21, АС = 20; ∠АСМ = 30°.

Найти: Sполн.

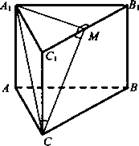
Решение: Угол между А1С и плоскостью ВВ1С1С равен 30°. Это угол между прямой А1С и ее проекцией на плоскость ВВ1С1С. А1М ⊥ В1С1, МС - проекция А1С на плоскость BB1CC1. ∠ACM = 30°. Рассмотрим ΔА1МС: А1М - высота и Рассмотрим ΔA1MC: (то есть ∠A1CM = 30°); А1С = 24 и (Ответ: )

№ 2. Дано: MABCD - правильная четырехугольная пирамида. DA = а; ∠BKD = 120°.

Найти: Sбок.

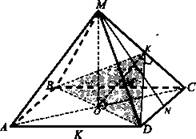
Решение: Угол между гранями BМС и DMC равен 120°; DK ⊥ MC; так как ΔВМС = ΔDMC, то BK ⊥ MC и ∠BKD - линейный угол двугранного угла с ребром МС; ha = MN; BD = а√2 (диагональ квадрата); ΔBKD - равнобедренный. Следовательно, ∠OKD = 60°, а ∠ODK = 30° и Рассмотрим ΔDMC: или Из ΔDKC: Из ΔMNC: (Ответ: )

III уровень (карточка 2)

№ 1. Дано: ABCDA1B1C1D1 - прямой параллелепипед. ABCD - параллелограмм; AD = 17 см; DC = 28, AC = 39; ∠A1DK = 45°.

Найти: Sполн.

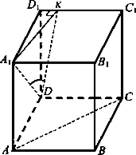
Решение. ; SABCD = 420. Угол между A1D и грань DD1C1C - это угол между A1D и проекцией A1D на плоскость DD1CC1. А1К ⊥ В1С1, то ∠A1DK= 45°. ΔA1KD - равнобедренный прямоугольный. A1K = DK; А1D найдем из ΔA1KD: А1А найдем из ΔA1AD.

(Ответ: )

№ 2. Дано: МАВС - правильная треугольная пирамида. АВ = ВС = АС = m. ∠AKC = 120°.

Найти: Sбок.

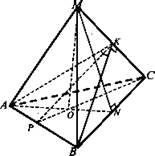
Решение: Угол между гранями АМВ и CMD равен линейному углу СК ⊥ MB, так как ΔАМВ = ΔСМВ, то АК ⊥ MB ⇒ ∠AKC - линейный двугранного угла при ребре MB. ∠AKC = 120°. MN - апофема боковой грани. Рассмотрим ΔАКС: равнобедренный. КР ⊥ АС и ΔMNB ~ ΔKBC (∠B - общий прямоугольника); КВ найдем из ΔCKB: (Ответ: )