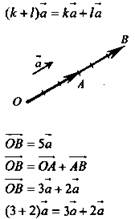Поурочные разработки по геометрии 10 класс
Умножение вектора на число - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО - ВЕКТОРЫ В ПРОСТРАНСТВЕ
Цели урока:
1) рассмотреть правило умножения вектора на число и основные свойства этого действия, а так же их применение при решении задач;
2) повторить и систематизировать знания по теме «Векторы»;
3) совершенствовать навыки выполнения действий над векторами.
Ход урока
I. Организационный момент
II. Контроль домашнего задания
На доске приготовить заранее чертежи к задачам № 327, 330 и вызвать двоих учеников для записи решений этих задач по уровням.
Кроме того, вызвать 1 ученика для записи и объяснения решения задачи № 335 и задачи № 340, если ребята справились с творческим заданием.
№ 327 (рис. 1)
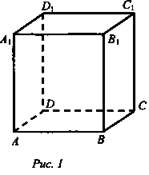
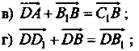
№ 330 (рис. 2)
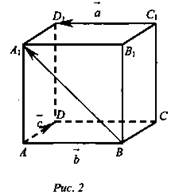
Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы ![]() соответственно через
соответственно через ![]() Изобразите на рисунке векторы:
Изобразите на рисунке векторы: ![]()
![]()
Решение:
![]()
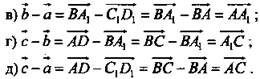
№ 335
![]()
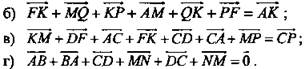
№ 340. Дана треугольная призма АВСА1В1С1. Укажите вектор ![]() , начало и конец которого являются вершинами призмы, такой, что
, начало и конец которого являются вершинами призмы, такой, что ![]() (рис. 3).
(рис. 3).
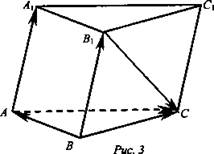
Решение: ![]() Поэтому нужно найти вектор
Поэтому нужно найти вектор ![]() такой, что
такой, что ![]() Из этого равенства находим:
Из этого равенства находим: ![]() или
или ![]()
В это время обсудить конспекты (выполненные дома) и повторить в вопросно-ответной форме материал предыдущего урока: правила сложения и вычитания векторов, свойства сложения, правило многоугольника для суммы нескольких векторов.
III. Актуализация опорных знаний (задания для самостоятельного выполнения с последующей проверкой)
№ 1. Найти:
(Ответы: ![]() ..
..
№ 2. Начертите неколлинеарные векторы ![]() Постройте векторы:
Постройте векторы: ![]()
IV. Изучение нового материала
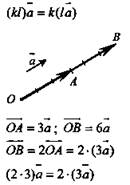
Сформулировать правило умножения вектора на число: ![]() если
если ![]() то
то ![]() при
при ![]() при k < 0. Если
при k < 0. Если ![]()
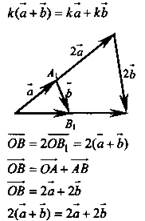
Подробно рассмотреть на примерах свойства умножения вектора на число и попросить ребят изобразить схему в тетрадях.
Умножение вектора на число
Сочетательный закон
|
Первый распределительный закон
|
Второй распределительный закон
|
Обратить внимание учащихся на то, что так же, как и в планиметрии, можно доказать следующее утверждение: если векторы ![]() коллинеарные и
коллинеарные и ![]() то существует число k, такое, что
то существует число k, такое, что ![]() (рекомендовать повторить доказательство учащимся, проявляющим интерес к геометрии)
(рекомендовать повторить доказательство учащимся, проявляющим интерес к геометрии)
V. Закрепление изученного материала
1) Решение задач из учебник.
Задача № 345
Точки Е и F - середины сторон АВ и ВС параллелограмма ABCD, а О - произвольная точка пространства. Выразите вектор ![]() через вектор
через вектор ![]() (рис. 4).
(рис. 4).
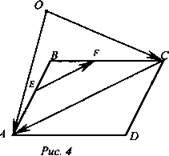
Решение: ![]() Так как EF - средняя линия треугольника ABC, то EF || АС и EF = 1/2AС. Поэтому
Так как EF - средняя линия треугольника ABC, то EF || АС и EF = 1/2AС. Поэтому ![]()
Задача № 347
а) Упростите выражение ![]()
Решение: ![]()
Задача № 348
Дан параллелепипед ABCDA1В1C1D1. (рис. 5).
Докажите, что ![]()
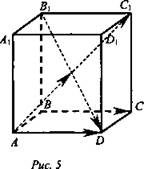
Решение: Из рисунка видно, что ![]()
![]()
Практическая работа (выполняется на листочках и сдается на проверку)
1) Отметьте на прямой а три точки А, В и М так, что: ![]()
![]()
2) Точка О - произвольная точка пространства. Для каждого случая из а-г 1) выразите вектор ![]() через векторы
через векторы ![]()
3) Точки А, В и М лежат на одной прямой, причем ![]() Найдите а, если для данных точек и произвольной точки О выполняется равенство:
Найдите а, если для данных точек и произвольной точки О выполняется равенство: ![]()
Постройте точки, удовлетворяющие каждому из этих равенств.
VI. Подведение итогов (блиц-опрос по вопросам):
- Что называется произведением ненулевого вектора на число?
- Что называется произведением нулевого вектора на число?
- Свойства умножения вектора на число.
- Справедливо ли утверждение: а) любые два противоположно направленных вектора коллинеарные; б) любые два коллинеарных вектора сонаправлены; в) любые два равных вектора коллинеарные; г) любые два сонаправленных вектора равны; д) если ![]()
Домашнее задание
I уровень - № 349, 351; II уровень - № 352, 353; творческое задание - № 385.
Решение домашних зада.
№ 351
Векторы ![]() а также
а также ![]() коллинеарные. Докажите, что коллинеарные векторы:
коллинеарные. Докажите, что коллинеарные векторы: ![]()
Доказательство:
1 способ
![]() - коллинеарные,
- коллинеарные, ![]() - коллинеарные.
- коллинеарные.
а) Прямые, на которых лежат ![]() либо параллельны, либо совпадают. Прямые, на которых расположены
либо параллельны, либо совпадают. Прямые, на которых расположены ![]() либо параллельны, либо совпадают. Две прямые, параллельные третьей, параллельны (
либо параллельны, либо совпадают. Две прямые, параллельные третьей, параллельны (![]() значит,
значит, ![]() ). Таким образом,
). Таким образом, ![]()
![]() расположены либо на нескольких прямых, либо на одной, то есть коллинеарные;
расположены либо на нескольких прямых, либо на одной, то есть коллинеарные;
б) ![]() - коллинеарные,
- коллинеарные, ![]() коллинеарен
коллинеарен ![]() значит,
значит, ![]() коллинеарен и
коллинеарен и ![]() и
и ![]() По условию,
По условию, ![]() коллинеарные, значит,
коллинеарные, значит, ![]() и
и ![]() тоже коллинеарные;
тоже коллинеарные;
в) Так как ![]() коллинеарные, то
коллинеарные, то ![]() коллинеарные. По условию
коллинеарные. По условию ![]() коллинеарные, тогда
коллинеарные, тогда ![]() и
и ![]() коллинеарные;
коллинеарные;
г) ![]() коллинеарные, поэтому
коллинеарные, поэтому ![]() коллинеарен
коллинеарен ![]() По условию
По условию ![]() коллинеарные, значит,
коллинеарные, значит, ![]() и
и ![]() коллинеарные.
коллинеарные.
2 способ
а) ![]() Отсюда
Отсюда ![]()
![]()
б) ![]() коллинеарные;
коллинеарные;
в) ![]() коллинеарные;
коллинеарные;
г) ![]() коллинеарные.
коллинеарные.
№ 352
Векторы ![]() коллинеарные.
коллинеарные.
Докажите, что векторы ![]() коллинеарные.
коллинеарные.
Доказательство: Примем ![]() По условию,
По условию, ![]()
![]() то есть
то есть ![]() где
где ![]() Равенство
Равенство ![]() доказывает, что
доказывает, что ![]() коллинеарные.
коллинеарные.
№ 353
Векторы ![]() коллинеарные.
коллинеарные.
Докажите, что векторы ![]() коллинеарные.
коллинеарные.
Доказательство: ![]() По условию,
По условию, ![]() то есть
то есть ![]()
![]() где
где ![]() Равенство
Равенство ![]() показывает коллинеарность
показывает коллинеарность ![]()
Творческое задание
№ 385
Отрезки, соединяющие середины противоположных сторон четырехугольника ABCD, пересекаются в точке М. Точка О - произвольная точка пространства. Докажите, что справедливо равенство ![]()
![]() (рис. 6).
(рис. 6).
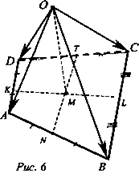
Доказательство:
1 способ.
Для произвольного ΔPQR ![]()
![]() Запишем равенство для каждой грани пирамиды OABCD:
Запишем равенство для каждой грани пирамиды OABCD: ![]()
![]() Сложив их, получим:
Сложив их, получим: ![]() или
или ![]()
Для ΔOKL имеем ![]() для ΔOMN имеем
для ΔOMN имеем ![]() Итак,
Итак, ![]() поэтому
поэтому ![]()