Поурочные разработки по геометрии 10 класс
Параллельные прямые в пространстве - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) рассмотреть взаимное расположение 2-х прямых в пространстве. Ввести понятие параллельных и скрещивающихся прямых;
2) доказать теоремы о параллельности прямых и параллельности 3-х прямых;
3) закрепить эти понятия на моделях куба, призмы, пирамиды.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать его цели.
II. Вспомнить материал из планиметрии о параллельности прямых (повторение)
1) Определение параллельных прямых;
2) Взаимное расположение 2-х прямых на плоскости (либо пересекаются, либо параллельны);
3) Как через точку А, заданную вне данной прямой а, провести прямую, параллельную а?
4) Сколько таких параллельных (к а через А) можно провести? Почему? (только одну, по аксиоме параллельных);
5) Аксиома параллельных (подчеркнуть, что через точку А вне прямой а можно провести единственную прямую, параллельную а).
III. Изучение нового материала
1) Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).
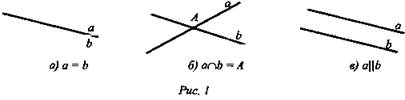
2) Перейдем к взаимному расположению 2-х прямых в пространстве. Как и в планиметрии, две различные прямые в пространстве либо пересекаются в одной точке, либо не пересекаются (не имеют общих точек). Однако второй случай допускает две возможности: прямые лежат в одной плоскости (параллельны) или прямые не лежат в одной плоскости. В первом случае они параллельны, а во втором - такие прямые называются скрещивающимися.
Даем определение. Сопровождаем показ параллельности, пересечения, скрещивания прямых хотя бы на модели куба, параллелепипеда, пирамиды (рисунки с обозначениями).
Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
3) Докажем теорему о параллельных прямых.
Теорема:
Дано: А; А ∈ а. Провести через А прямую b || а, доказать ее единственность (рис. 2).
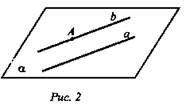
Доказательство:
По условию даны прямая а и не лежащая на ней точка А. По ранее доказанной теореме через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Проведем плоскость α. Теперь в плоскости а через току А проведем прямую b || а, а из планиметрии известно, что через точку А вне прямой а можно провести прямую, параллельную данной, и притом только одну. Теорема доказана.
В дальнейшем нам понадобятся такие понятия: два отрезка называются параллельными, если они лежат на параллельных прямых, аналогично определяются параллельность отрезка и прямой, параллельность двух лучей.
Докажем лемму о пересечении плоскости параллельными прямыми, которой будем пользоваться в дальнейшем.
Лемма: а || b; α; а ∩ α = А (рис. 3).
Доказать, что b ∩ α.
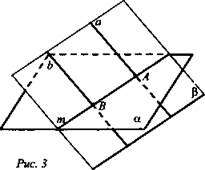
Доказательство:
1. а || b определяют плоскость β.
2. Получили, что α и β имеют общую точку А, по аксиоме А3 ![]() поэтому
поэтому ![]() поэтому В ∈ α следовательно, В ∈ b, b ∈ α.
поэтому В ∈ α следовательно, В ∈ b, b ∈ α.
Докажем, что прямая b не имеет других общих точек с плоскостью α, кроме точки В. А это означало бы, что b ⊂ α.
Если бы прямая b имела еще хотя бы одну общую точку с плоскостью α, то она целиком бы лежала в плоскости α, а это значит, что она была бы общей прямой плоскости α и плоскости β, то есть b ≡ m, но это невозможно, так как по условию а || b, и а ⊂ m. Значит, b ⊂ α = B. Лемма доказана.
4) Из планиметрии известно:
Если две прямые параллельны третьей прямой, то они параллельны.
Аналогичное утверждение имеет место и для 3-х прямых в пространстве.
Теорема: Дано: а || с; b || с (рис. 4). Доказать, что а || b, то есть 1) лежат в одной плоскости; 2) не пересекаются.
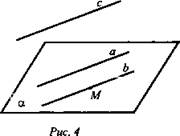
Доказательство: 1) Возьмем на прямой b точку М и через а и М проведем плоскость α. Докажем, что b ⊂ α.
Если допустить, что b ∩ α, то по лемме о пересечении плоскости параллельными прямыми прямая с ∩ α, но а || с, значит, а ∩ α, что невозможно, так как а ⊂ α.
2) Прямая a ∩ b, так как в противоположном случае через точку их пересечения проходили бы две прямые (а и b), параллельные с, что невозможно. И значит, а || b и теорема доказана.
IV. Закрепление изученного материал.
Задача № 17
Дано: М - середина BD; N - середина CD; Q - середина АС; Р - середина АВ; AD = 12 см; ВС = 14 см (рис. 5).
Найти: PMNQP - ?
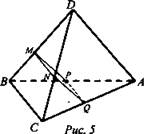
Решение:
1. MN || BC по составу средней линии ⇒ MN || PQ; PQ || BC.
2. РМ || AD по составу средней линии ⇒ PM || QN; NQ || DA.
3. По определению MNQP - параллелограмм.
4. PQ = 7; РМ = 6 ⇒ РMNQP = 2(7 + 6) = 26. (Ответ: 26 см.)
V. Подведение итогов
Домашнее задание
П. 4, 5, теоремы.
Задача № 16
Дано: ![]()
![]() (рис. 6).
(рис. 6).
Доказать: с ⊂ α.
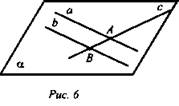
Доказательство: По условию а ∩ с = А; b ∩ с = В, значит А ∈ α и В ∈ α, так как а ⊂ α и b ⊂ α, по А2 с ⊂ α, что и требовалось доказать.