Урок 63. Теоретический тест с последующей самопроверкой - Контрольные и самостоятельные работы - ПРИЛОЖЕНИЯ

Вариант I

1. Какое из следующих утверждений верно: а) любые четыре точки лежат в одной плоскости; б) любые три точки лежат в одной плоскости; в) любые четыре точки не лежат в одной плоскости; г) через любые три точки проходит плоскость; д) через любые три точки проходит плоскость и притом только одна.

2. Сколько общих точек могут иметь две различные плоскости? а) 2; б) 3; в) несколько; г) бесконечно много; д) бесконечно много или ни одной.

3. Точки А, В, С лежат на одной прямой, точка D не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных плоскостей при этом получилось? а) 2; б) 3; в) 1; г) 4; д) бесконечно много.

4. Если три точки не лежат на одной прямой, то положение плоскости в пространстве:

а) не определяются в любом случае; б) определяются, но при дополнительных условиях; в) определяются в любом случае; г) ничего сказать нельзя; д) другой ответ.

5. Выберите верное утверждение: а) если одна точка прямой лежит в плоскости, то все точки прямой лежат в этой плоскости; б) через прямую и не лежащую на ней точку проходит плоскость, и притом только одна; в) через две перекрещивающиеся прямые плоскость провести нельзя; г) любые две плоскости не имеют общих точек; д) если четыре точки не лежат в одной плоскости, то какие-нибудь три из них лежат на одной прямой.

6. Назовите общую прямую плоскостей AFD и DEF: a) AD; б) DE; в) определить нельзя; г) DF; д) AF.

7. Какую из перечисленных плоскостей пересекает прямая EF? a) ABC; б) АА1D; в) ВВ1С1 г) AEF; д) В1С1С.

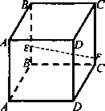
8. Через точку М, не лежащую на прямой а, провели прямые, пересекающие прямую а. Тогда: а) эти прямые не лежат в одной плоскости; б) эти прямые лежат в одной плоскости; в) никакого вывода сделать нельзя; г) часть прямых лежат в плоскости, а часть - нет; д) все прямые совпадают с прямой а.

9. Прямая а лежит в плоскости α и пересекает плоскость β. Каково взаимное расположение плоскостей α и β? а) определить нельзя; б) они совпадают; в) имеют только одну общую точку; г) не пересекаются; д) пересекаются по некоторой прямой.

10. Точки А, В, С не лежат на одной прямой. М ∈ АВ, К ∈ AC, X ∈ МК. Выберите верное утверждение: а) X ∈ АВ; б) X ∈ АС; в) X ∈ ABC; г) Х и М совпадают; д) точки Х и К совпадают.

Вариант II

1. Что можно сказать о взаимном расположении плоскостей, которые имеют три общие точки, не лежащие на одной прямой? а) пересекаются; б) ничего сказать нельзя; в) не пересекаются; г) совпадают; д) имеют три общие точки.

2. Какое из утверждений верно? а) если две точки треугольника лежат в плоскости, то и весь треугольник лежит в плоскости; б) прямая, лежащая в плоскости треугольника пересекает его стороны; в) любые две плоскости имеют только одну общую точку; г) через две точки проходит плоскость, и притом только одна; д) прямая лежит в плоскости треугольника, если она пересекает две прямые, содержащие стороны треугольника.

3. Могут ли две различные плоскости иметь только две общие точки? а) никогда; б) могут, но при дополнительных условиях; в) всегда имеют; г) нельзя ответить на вопрос; д) другой ответ.

4. Точки К, L, М лежат на одной прямой, точка N не лежат на ней. Через каждые три точки проведена плоскость. Сколько различных плоскостей при этом получилось, а) 1; б) 2; в) 3; г) 4; д) бесконечно много.

5. Выберите верное утверждение: а) через любые три точки проходит плоскость и притом только одна; б) если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости; в) если две плоскости имеют общую точку, то они не пересекаются; г) через прямую и точку лежащую на ней проходит плоскость и притом только одна; д) через две пересекающиеся прямые плоскость провести нельзя.

6. Назовите общую прямую плоскостей РВМ и МАВ: а) РМ; б) АВ; в) РВ; г) ВМ; д) определить нельзя.

7. Какую из перечисленных плоскостей пересекает прямая РМ (рис. 2)? a) DD1C1; б) D1PM1; в) B1PM; г) ABC; д) CAD.

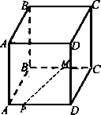
8. Две плоскости пересекаются по прямой с. Точка М лежит только в одной из плоскостей. Что можно сказать о взаимном расположении точки М и прямой с? а) вывода сделать нельзя; б) прямая с проходит через точку М; в) М ∈ с; г) прямая с не проходит через точку М; д) другой ответ.

9. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Что можно сказать о взаимном расположении прямых а, b и с? а) они лежат в разных плоскостях; б) а и b лежат в одной плоскости, а прямая с в ней не лежит; в) все прямые лежат в одной плоскости; г) ничего сказать нельзя; д) прямая с совпадает с одной из прямых.

10. Прямые а и b пересекаются в точке О. А ∈ а, В ∈ b, У ∈ АВ. Выберите верное утверждение: а) точки О и У лежат в разных плоскостях; б) прямая ОУ || а; в) прямые а, b и точка У лежат в одной плоскости; г) точки О и У совпадают; д) У и А совпадают.