Поурочные разработки по геометрии 10 класс
Решение задач по теме «Параллельность прямой и плоскости» - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) закрепить теоретический материал;
2) закрепить навык применения изученных теорем при решении задач;
3) воспитывать интерес к геометрии.
Ход урока
I. Организационный момент
Сообщить тему и цели урока.
II. Проверка домашнего задания
Решение задач № 19, 21 подготовить на доске (2 ученика).
Решение задачи № 18 (a) - один из учащихся комментирует решение.
III. Актуализация знаний учащихся. Подготовить у доски доказательство теорем:
1 – о параллельных прямых;
2 – о параллельности трех прямых;
3 – о параллельности прямой и плоскости.
Фронтальный опрос
1) Какие прямые в пространстве называются параллельными?
2) Всегда ли через две параллельные прямые можно провести - плоскость? А через две пересекающиеся прямые? (Да, да.)
3) В пространстве дано число n параллельных между собой прямых. Известно, что никакие три из них не лежат в одной плоскости. Сколько различных плоскостей можно провести через эти прямые? (Число n плоскостей.)
4) Сформулируйте лемму о пересечении плоскости параллельными прямыми.
5) Каково может быть взаимное расположение прямой и плоскости в пространстве?
6) В каком случае прямая параллельна плоскости?
IV. Решение задач
1) Решение у доски с записью в тетрадя.
Задача № 22
Дано: A ∈ α, В ∈ α, С ∈ α; AM = МС; BN = NC.
Доказать: MN || α.
Доказательство: MN || АВ (по свойству средней линии), АВ ∈ α; MN || α по признаку.
Перед решением задачи № 26 дать понятие отрезка, параллельного плоскости.
«Отрезок параллелен плоскости, если прямая, содержащая этот отрезок, параллельна плоскости».
Задача № 26
Дано: АС || α, АВ ∩ α = М; СВ ∩ α = N (рис. 1).
Доказать: ΔАВС ~ ΔMBN.
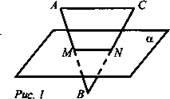
Доказательство:
1. Докажем, что AC || MN;
![]()
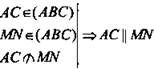 (по определению).
(по определению).
2. Так как АС || MN ⇒ ΔАВС ~ ΔMBN.
2) Самостоятельное решение задач по уровням
I уровень
Отрезок АВ не пересекает плоскость α. Через середину отрезка С и концы отрезка А и В проведены прямые, параллельные между собой и пересекающие плоскость α в точках А1, В1, С1.
Вычислить длину отрезка СС1, если АА1 = 5, BB1 = 7.
Дано: ![]() АА1 = 5 см, ВВ1 = 7 см (рис. 2).
АА1 = 5 см, ВВ1 = 7 см (рис. 2).
Найти: СС1.
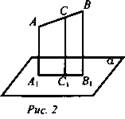
Решение:
1. Докажем, что A1, С1 и В1 лежат на одной прямой. (АА1, ВВ1) = β, β ∩ а = А1В1. Докажем, что С1 ∈ А1В1.
2. Пусть С1 ∈ А1В1, тогда CC1 ∩ β = c, с - прямая пересечения; ![]() по лемме АА1 ∩ β. Получили противоречие, значит, С1 ∈ А1В1.
по лемме АА1 ∩ β. Получили противоречие, значит, С1 ∈ А1В1.
3. Так как А1А || ВВ1, значит, А1АВВ1 - трапеция, СС1 - средняя линия ![]() (Ответ: 6 см.)
(Ответ: 6 см.)
II уровень
Точка М лежит на отрезке АВ. Отрезок АВ пересекается с плоскостью α в точке В. Через А и М проведены параллельные прямые, пересекающие α в точках А1 и M1.
а) Докажите, что А1, М1 и В лежат на одной прямой.
б) Найдите длину отрезка АВ, если АА1 : ММ1 = 3 : 2, AM = 6.
Дано: ![]()
![]() (рис. 3).
(рис. 3).
Докажите: М1 ∈ А1В.
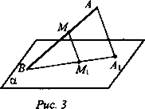
Найдите: АМ = 6.
Решение:
1. ![]() Предположим, М1 ∈ А1В, тогда
Предположим, М1 ∈ А1В, тогда ![]() значит,
значит, ![]() что противоречит условию.
что противоречит условию.
2. ![]()
![]() (Ответ: 12 см.)
(Ответ: 12 см.)
V. Подведение итогов
Домашнее задание
I уровень: № 24, 28.
II уровень: № 31, дополнительная задача № 1.
I уровень
Задача № 24
Дано: ABCD - трапеция М ∉ (ABC) (рис. 4).
Доказать: AD || (ВМС).
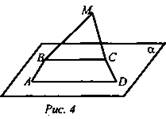
Доказательство: AD || ВС (по определению трапеции); ВС ∈ (ВМС), значит AD || (ВМС) по признаку.
Задача № 28
Дано: D ∈ AB, Е ∈ AC, DE = 5; ![]() (рис. 5).
(рис. 5).
Найдите: ВС.
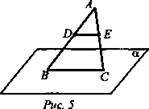
Решение:
1) ![]()
2) 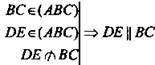 по определению.
по определению.
3) ΔАВС ~ ΔADE (по двум углам.
![]() (Ответ:
(Ответ: ![]() )
)
II уровен.
Задача № 31
Дано: α || ВС, АК = ВК, К ∈ α (рис. 6).
Доказать: α ∩ АС = М; АМ = СМ.
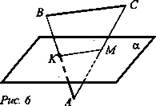
Доказательство:
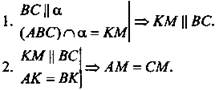
Дополнительная задача
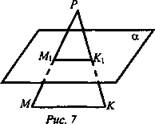
Дан ΔМКР. Плоскость, параллельная прямой МК, пересекает МР в точке М1, РК - в точке К1. Найдите М1К1, если МР : М1Р = 12 : 5, МК = 18 см.
Дано: ![]()
![]() (рис. 7).
(рис. 7).
Найти: М1К1.
Решение:
1. ![]()
2. ΔМРК ~ ΔМ1РК1 (по двум углам).
![]() (Ответ: 7,5 см.)
(Ответ: 7,5 см.)