Поурочные разработки по Геометрии 11 класс
Угол между векторами. Скалярное произведение векторов - урок 2 - Скалярное произведение векторов - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Цели урока:
- повторить с учащимися вопросы теории и рассмотреть основные свойства скалярного произведения;
- сформировать умения вычислять скалярное произведение векторов и находить угол между векторами.
Ход урока
I. Организационный момент
II. Проверка домашнего задания
Заслушать ход решения задачи № 443 (в) и дополнительной задачи (III уровень) по заранее подготовленным на доске решениям.
Учащимся дается задание: внимательно выслушать решение задач и быть готовыми ответить на вопрос: «Верно ли решена задача? Какие замечания к решению у тебя есть?»
Задача № 443 б).
Решение:
![]()
(Ответ: -2а2.)
III. Математический диктант (см. приложение)
После написания диктанта проводится самопроверка и обсуждение задач, с которыми не справилось большинство учащихся.
IV. Изучение нового материала
1. Задание:
- Запишите формулу длины вектора в координатах;
- Выразите ![]() из определения скалярного произведения.
из определения скалярного произведения.
- Пусть ![]()
Выразите ![]() в координатах.
в координатах.
Имеем 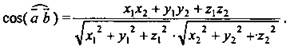
2. Основные, свойства скалярного произведения. (По усмотрению учителя некоторые можно доказать.)
Для любых векторов ![]() и любого числа k справедливы равенства:
и любого числа k справедливы равенства:
1) ![]() причем
причем ![]() при
при ![]()
2) ![]() (переместительный закон).
(переместительный закон).
3) ![]() (распределительный закон).
(распределительный закон).
4) ![]() (сочетательный закон).
(сочетательный закон).
Рассмотрим для примера свойство 3. Введем прямоугольную систему координат и рассмотрим произвольные векторы ![]()
![]() Воспользуемся формулой скалярного произведения в координатах и тем, что координаты вектора
Воспользуемся формулой скалярного произведения в координатах и тем, что координаты вектора ![]() равны суммам соответствующих координат векторо.
равны суммам соответствующих координат векторо.
![]()
![]()
3. Следует обратить внимание учащихся на то, что распределительный закон имеет место для любого числа слагаемых, а скалярное произведение, в котором каждый из сомножителей является суммой векторов, можно вычислить по правилу умножения многочленов.
Рассмотрим, например, скалярное произведение ![]() Положим
Положим ![]() Тогда
Тогда ![]()
![]() Таким образом,
Таким образом, ![]()
![]() Свойства скалярного произведения используются в процессе решения задач.
Свойства скалярного произведения используются в процессе решения задач.
V. Закрепление изученного материала
1. Решение задач по готовому чертежу (рис. 1).
Дано: ![]()
Найти: ![]()
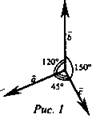
Решение.
![]()
![]() (Ответ:
(Ответ: ![]() )
)
Задача № 444 б), д)
Решение: ![]()
Вопрос: Какими являются эти векторы? ![]()
![]() (Ответ: б) 0; д) √3.)
(Ответ: б) 0; д) √3.)
Задача № 445 д).
Дано: ![]()
Вычислить: ![]()
Решение: ![]()
![]()
![]() (Ответ: 28.)
(Ответ: 28.)
Вопрос: Какие свойства скалярного произведения использовали при решении этой задачи?
Задача № 446 а).
Дано: ![]()
Найти: вид ![]()
Решение: ![]()
![]() если 90° < а < 180°. Значит,
если 90° < а < 180°. Значит, ![]() тупой. (Ответ: тупой.)
тупой. (Ответ: тупой.)
2. Самостоятельное решение задач с последующей проверкой.
I уровень
Задача № 449.
Дано: ![]()
Найти: значение m, при котором векторы ![]() перпендикулярны.
перпендикулярны.
Решение: ![]() если
если ![]()
![]() (Ответ: 4.)
(Ответ: 4.)
II уровень
Дано: ![]()
Найти: ![]()
Решение:
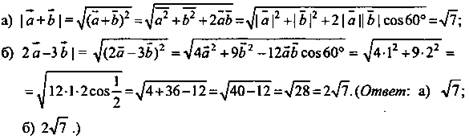
III уровень
Даны три силы ![]() приложенные к одной точке. Вычислите работу, производимую равнодействующей этих сил, когда точка их приложения, двигаясь прямолинейно, перемещается из А(5; 3; -7) в В(4; 1;-4).
приложенные к одной точке. Вычислите работу, производимую равнодействующей этих сил, когда точка их приложения, двигаясь прямолинейно, перемещается из А(5; 3; -7) в В(4; 1;-4).
Решение:
1. Найдем равнодействующую ![]()
2. Найдем вектор перемещения ![]()
![]() (Ответ: А = 7.)
(Ответ: А = 7.)
Все задачи проверяются по готовым решениям.
VI. Подведение итогов
- Итак, в ходе сегодняшнего урока мы рассмотрели основные свойства скалярного произведения векторов, научились применять их для вычисления скалярного произведения и нахождения углов между векторами.
Домашнее задание
I уровень: № 445 (г); 446 (в); 451 (д).
II уровень: № 453; 459 (а); 454.
III уровень: № 459 б).
Дополнительные задачи
Задача № 1. Дан куб ABCDA1B1C1D1 ребро которого равно 1.
Найдите угол между векторами ![]() где точка М - середина ребра СС1.
где точка М - середина ребра СС1.
Решение:
1 способ
Введем систему координат (рис. 2).
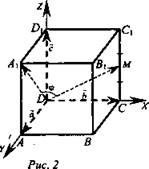
![]()
![]()
2 способ
![]()
![]() (Ответ:
(Ответ: ![]() )
)
Задача № 2
Дано: ![]()
Найти: ![]()