Цилиндр. Решение задач - Цилиндр - ЦИЛИНДР, КОНУС И ШАР

Цели урока:

- формировать навыки решения задач на нахождение элементов цилиндра, площади поверхности цилиндра;

- закрепить знания, умения учащихся по изучаемой теме;

- развивать самостоятельность учащихся в работе над задачами. Используемый дополнительный материал: задачи на готовых чертежах.

Ход урока

I. Организационный момент

Объявление темы и цели урока.

II. Актуализация знаний учащихся

Устная работа с классом.

1. Укажите среди окружающих вас предметов объекты, имеющие цилиндрическую форму.

2. Дайте определение цилиндра и его основных элементов.

3. Что такое осевое сечение цилиндра? Каков его вид?

4. Может ли осевое сечение быть: а) прямоугольником; б) квадратом; в) трапецией? Почему?

5. Цилиндр катится по плоскости. Какая фигура получается при движении его оси?

Проверка домашнего задания (три ученика работали у доски во время устной работы класса).

№ 522 (рис. 1).

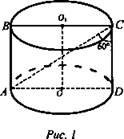
Решение:

1. ABCD - прямоугольник.

2. ΔACD - прямоугольный.

3.

4.

5.

(Ответ: )

№ 524 (рис. 2).

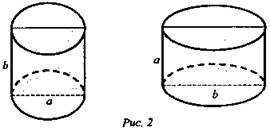
Решение: Осевые сечения равны, значит, при наложении они совпадут. Но высоты цилиндров не равны: а ≠ b. (Ответ: нет.)

№ 526 (рис. 3).

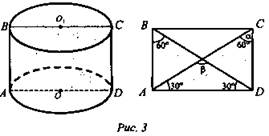
Решение:

1.

2.

3.

4.

(Ответ: а) 30°; б) 60°.)

Решение задач по готовым чертежам.

I уровень - устно с обсуждением решения: № 1, 2, 3.

II уровень - самостоятельное решение с самопроверкой по готовым ответам: № 4, 5, 6.

Задача № 1 (рис. 4).

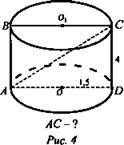
Решение:

1. OD = R, AD = 3.

2. ΔADC - прямоугольный. Так как AD = 4, то АС = 5 (пифагорова тройка).

(Ответ: 5.)

Задача № 2 (рис. 5).

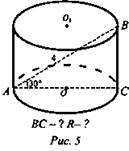
Решение:

1. ΔАВС - прямоугольный.

2. Так как ∠BAC = 30°, то ВС = 1/2АВ, т. е. ВС = 2.

3.

4.

(Ответ: 2; √3.)

Задача № 3 (рис. 6).

Дано: О1А = 5, AA1 = 15, АВ = 17.

Найти: расстояние между OO1 и АВ.

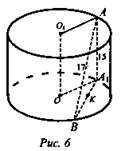
Решение:

1. ΔАА1В - прямоугольный; по теореме Пифагора ДП: ОК, К - середина ВА1.

2. ОK ⊥ A1B (так как ОК - расстояние между ОО1 и АВ:

3. По теореме Пифагора из ΔA1KO:

(Ответ: 3.)

Задача № 4. (рис. 7).

Найти: SABCD.

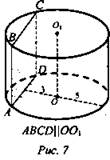
Решение:

1. АО = 5 - дополнительное построение.

2.

3. ABCD - прямоугольник.

4.

(Ответ: 80.)

Задача № 5.

Дано:

Найти: Н/2R.

Решение:

1.

2.

(Ответ: 1/8.)

Задача № 6 (рис. 8).

Дано: ABCD - осевое сечение.

Найти:

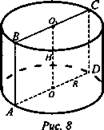
Решение:

1. Sбок. = 2πRH, ABCD - прямоугольник.

2.

3.

(Ответ: π.)

III. Решение зада.

№ 530 (рис. 9).

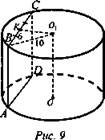
Решение:

1. ABCD - квадрат.

2. Так как O1К - расстояние от точки О до ABCD, то О1К ⊥ ABCD, О1К ⊥ ВС.

3. АВ = ВС = 12 см ⇒ ВК = 6 см.

4. BO1 = 10 см.

5. ΔВКО1 - прямоугольный, по теореме Пифагора.

(Ответ: 8 см.)

№ 533 (рис. 10).

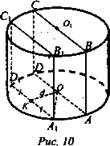
Решение:

1. SABCD = S.

2.

3. ΔОКА1 - прямоугольный, ∠К = 90°. ОA1 =R.

4.

5.

(Ответ: )

№ 537 (рис. 11).

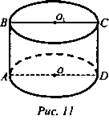
Решение:

1. Sбок. = 2πRH.

2. d = AD = 1 (м).

3.

4.

(Ответ: π2 м2.)

IV. Подведение итогов

- На этом уроке мы отрабатывали навыки решения задач на нахождение элементов цилиндра и совершенствовали полученные знания при решении задач.

Домашнее задание

П. 53, 54. I уровень - № 527, 531. II уровень - № 531, 544, 601.

Решение задач из домашнего задания.

№ 527 а) (рис. 12).

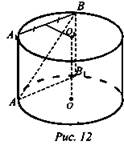
Решение:

1. Достроим плоскость, содержащую АВ так, чтобы А1ВВ1А || OO1.

2. АА1ВВ1 - прямоугольник.

3. O1К ⊥ A1B, О1К - расстояние от OO1 до АА1ВВ1, так как O1К ⊥ АА1ВВ1, К - середина А1В.

4. r = 10 дм, d = O1K = 8 дм, AB = 13 дм.

5.

6. (так как ΔAA1В - прямоугольный).

(Ответ: 5 дм.)

№ 531 (рис. 13).

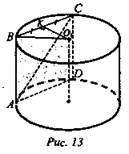
Решение:

1. ABCD || ОО1.

2. O1К- расстояние от ОО1 до ABCD. O1К = 9 дм, К-середина ВС.

3. SABCD = 240 дм2.

4. 240 = 10 · ВС, ВС = 24 дм, ВК = 12 дм.

5. ΔВКО1 - прямоугольный, (Ответ: 15 дм.)

№ 544 (рис. 14).

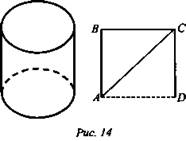
Решение:

1. Sосн. = πR2.

2.

3.

4.

(Ответ: )

№ 601 (рис. 15).

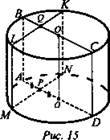
Решение:

1) ABCD - осевое сечение; OA = R, P- середина ОА; MLKN ⊥ ОА;

2) ABCD и MLKN - прямоугольники;

3)

4) OP = AP = R/2.

5) ΔМРО - прямоугольный

6)

7)

8)

(Ответ: )