Поурочные разработки по Геометрии 11 класс
Разные задачи на многогранники, цилиндр, конус и шар - урок 2 - Сфера - ЦИЛИНДР, КОНУС И ШАР
Цели урока:
- закрепить основные понятия по изученной теме;
- совершенствовать навык решения задач на комбинацию: призмы и сферы; конуса и пирамиды.
Ход урока
I. Проверка домашнего задания
Два ученика у доски показывают решение № 635 (а) и № 637 (а).
В целях экономии времени рекомендуется подготовить чертеж, краткое решение и основную идею доказательства.
За время подготовки учащихся провести фронтальный опрос класса по вопросам:
- Какой многогранник называется вписанным в сферу?
- Какая сфера называется вписанной в многогранник?
- Какой многогранник называется описанным около сферы?
- Какая сфера называется описанной около многогранника?
- Где находится центр шара, вписанного в пирамиду?
Задача № 635 а). Дано: SABCD - правильная пирамида, ∠ASD = α; сфера (O1; R) вписанная в пирамиду (рис. 1).
Найти: Sбок. - ?
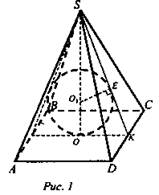
Решение: Пусть сторона основания АВ = AD = а, высота боковой грани SK = hа - апофема.
1. ![]()
2. ΔSO1E ∞ ΔSKO (по 2 углам) ![]()
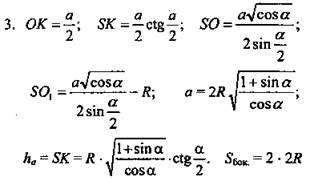
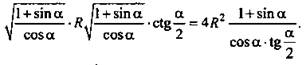
(Ответ: 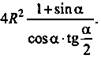 )
)
Задача № 637 а). Дано: RPQR1P1Q1 - правильная призма, AB - высота; сфера (О; R), описанная около призмы (рис. 2).
Доказать: АО = OB; R = ОР = ОР1.
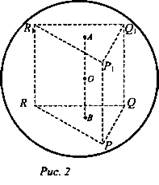
Доказательство: В основаниях призмы лежат равные равносторонние треугольники. Примем А и В центры оснований. Все точки, лежащие на перпендикуляре к верхнему основанию призмы, проведенном через точку А, равноудалены от вершин ΔP1Q1R1. Аналогично с нижним основанием. Т.к. призма правильная, то ΔP1Q1R1 и ΔPQR проектируется один на другой, поэтому точки В и А проектируются друг в друга. Значит, А В перпендикуляр к плоскостям оснований призмы. Отрезок АВ есть геометрическое место точек, равноудаленных от вершин ΔP1Q1R1 и ΔPQR, середина АВ - точка О равноудалена от вершин треугольников на расстоянии R, равны радиусу описанной около призмы сферы.
Так как АО = ОВ и OP = ОР1 = R.
II. Актуализация опорных знаний
- Какая призма называется вписанной в сферу?
- Какая призма называется описанной около сферы?
- Какая призма называется правильной?
- Около всякого ли прямоугольника можно описать окружность?
- Где находится центр этой окружности?
- Во всякий ли прямоугольник можно вписать окружность?
- А в какой можно?
III. Решение задач
1. Теория на комбинацию: призма и шар.
а) Шар, вписанный в призму.
- Шар можно вписать в прямую призму, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
- Центр вписанного шара лежит на середине высоты прямой призмы, проходящей через центры окружностей вписанных в основания призмы, а радиус шара равен радиусу окружности, вписанной в основание призмы.
б) Шар, описанный около призмы.
- Около призмы можно описать шар тогда и только тогда, когда призма прямая и около основания можно описать окружность.
- Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведенной через центр окружности, описанной около основания.
2. Задача № 632.
Дано: АВСА1В1С1 - правильная призма, О и O1 - центры оснований призмы; сфера (S; R) вписанная в призму (рис. 3).
Доказать: OS = SO1.
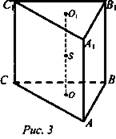
Доказательство: Сфера касается всех граней призмы, центр ее должен быть равноудален от оснований, т.е. лежать на середине высоты призмы. Отрезок OO1, соединяющий центры оснований, является высотой призмы и все точки, лежащие на отрезке OO1, равноудалены от боковых граней призмы. (О и О1 - центры вписанных в основания окружностей.) Таким образом, середина O1O, точка S, является центром сферы.
Задача № 634 а). Дано: ABCDA1B1C1D1 - куб, сфера (О; R) вписанная в куб (рис. 4).
Найти: S полной поверхности куба.
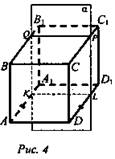
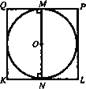
Решение: Рассмотрим сечение KLPQ, где К, L, Р, Q - середины АА1, ВВ1, СС1 и DD1 соответственно. В сечении получим квадрат и вписанную в него окружность, ее радиус равен радиусу сферы. Пусть ребро куба равно а, а = 2R. Площадь одной грани равна а2 или 4R2 . Sп.п. = 6 · 4R2 = 24R2. (Ответ: 24R2.)
Задача № 639 б). Дано: Вписанная правильная шестиугольная призма, Н1Н2 = R высота призмы; сфера (О; R) (рис. 5).
Найти: S полной поверхности призмы.
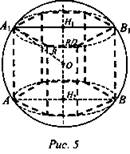
Решение: Н1 и Н2 - центр оснований призмы.
Рассмотрим сечение призмы плоскостью, проходящей через диаметр оснований призмы перпендикулярного основаниям призмы. Получим прямоугольник АА1В1В. Из прямоугольного ΔОА1Н1: 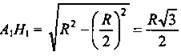 (по теореме Пифагора). А1Н1 - радиус описанной окружности около основания призмы, а в правильном шестиугольнике его сторона равна радиусу описанной около него окружности. Сторона основания а.
(по теореме Пифагора). А1Н1 - радиус описанной окружности около основания призмы, а в правильном шестиугольнике его сторона равна радиусу описанной около него окружности. Сторона основания а. ![]() площадь грани
площадь грани ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
Задача № 630. Дано: конус, SO - высота; SABCD - пирамида, вписанная в конус, ABCD - прямоугольник; SO = 12 см, АВ = 8 см, ВС = 6 см (рис. 6).
Найти: ![]()
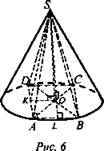
Решение: SO ⊥ (ABCD), ОА = ОВ = r. Ребра пирамиды равны образующим конуса и лежат на поверхности конуса. ![]() ;
; ![]() Найдем площадь полной поверхности конуса.
Найдем площадь полной поверхности конуса. ![]() Из прямоугольного ΔSOA:
Из прямоугольного ΔSOA: ![]()
![]()
![]() Боковые грани попарно равны. Проведем OK ⊥ DA, OL ⊥ AB, отрезки SK и SL. По теореме о трех перпендикулярах SK ⊥ DA и SL ⊥ АВ.
Боковые грани попарно равны. Проведем OK ⊥ DA, OL ⊥ AB, отрезки SK и SL. По теореме о трех перпендикулярах SK ⊥ DA и SL ⊥ АВ. ![]() Из ΔSOK: SK =
Из ΔSOK: SK = ![]() Из ΔSOL:
Из ΔSOL: ![]()
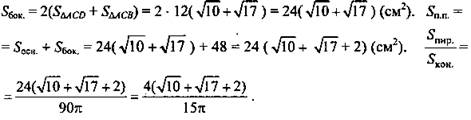
(Ответ: ![]() )
)
IV. Подведение итогов
Проводится закрепление умения решать задачи по теме урока.
Домашнее задание
Подготовить теорию по изученной теме, № 634 б) и № 639 а).