Поурочные разработки по Геометрии 11 класс
Объем прямоугольного параллелепипеда. Объем прямоугольной призмы, основанием которой является прямоугольный треугольник - Объем прямоугольного параллелепипеда - ОБЪЕМЫ ТЕЛ
Цели урока:
- повторить свойства объемов, объем прямоугольного параллелепипеда;
- рассмотреть следствие об объеме прямой призмы, основанием которой является прямоугольный треугольник.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
1. Теоретический опрос.
Подготовить у доски доказательство теоремы об объеме прямоугольного параллелепипеда (в случае когда а, b, с - конечные десятичные дроби).
2. Проверка домашнего задания.
а) № 652 - ученик на доске записывает решение задачи.
б) Индивидуально проверить домашние задачи № 648 (в, г), 649 (в) из рабочей тетради (выборочно, 4-5 учащихся).
Задача № 652. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед. АС1 = 13 см, BD = 12 см, ВС1 = 11 см (рис. 1).
Найти: V.
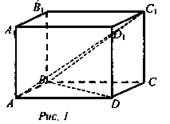
Решение: V = AD · АВ · АА1.
1) Диагональ и измерения (а, b, с) прямоугольного параллелепипеда связаны соотношением: AD2 + АВ2 + АА2 = АС12, так как AD2 + АВ2 = BD2, имеем 122 + АА12 = 132, АА1 = 5 см.
2) ![]()
![]()
3) ![]() Тогда
Тогда ![]()
![]()
(Ответ: 240√2 см3.)
Задача № 648 в), г).
в) ![]()
г) ![]()
(Ответ: 3,2√5.)
Задача № 649 б). Дано: DE = 1 см, E - середина ребра AB куба ABCDA1B1C1D1 (рис. 2).
Найти: VABCDA1B1C1D1.
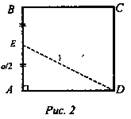
Решение: Рассмотрим основание ABCD куба ABCDA1B1C1D1. Пусть ребро куба равно а. Из ΔEAD: ![]()
![]() (Ответ:
(Ответ: ![]() .
.
3. Остальные решают задачу по готовому чертежу (на доске).
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед. B1D = 10√2 (рис. 3).
Найти: V.
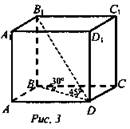
Решение:
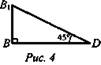
1. Рассмотрим ΔBB1D - прямоугольный (рис. 4). ΔBB1D: ![]() значит,
значит, ![]() BB1 = 10 = h.
BB1 = 10 = h.
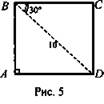
2. (рис. 5). ΔBCD: ∠B = 30°, ∠C= 90°, значит, ![]()
![]()
3. ![]()
III. Изучение нового материала
Рассмотреть следствие № 2 и доказать его.
Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.
1. Прочитать самостоятельно доказательства следствия № 2.
2. Запись формулы объема в тетради.
![]()
Обсуждение (материала) доказательства.
IV. Решение задачи
Задача № 653. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, диагональ D1B = 18 составляет угол в 30° с плоскостью боковой грани, и угол в 45° с боковым ребром (рис. 6).
Найти: V.
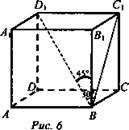
Решение: BC1 - проекция D1B на плоскость боковой грани BB1С1С, поэтому ∠D1BC1 = 30°, ∠D1BB1 = 45°.
1. Рассмотрим ΔD1C1B: ∠D1C1B = 90° (рис. 7). ![]()
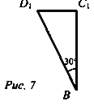
2. Рассмотрим ΔD1B1B - прямоугольный: ![]()
3. Диагональ (d) и измерения (а, b, с) прямоугольного параллелепипеда связаны соотношением: ![]()
![]()
![]() (Ответ: V = 729√2 см3.)
(Ответ: V = 729√2 см3.)
V. Подведение итогов
Выставление оценок.
VI. Домашнее задание
Гл. VII. § 1. п. 63, 64. (теория); № 656, 658. Вопрос № 1. стр. 169.