Повторение. Параллельность прямых, параллельность прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ

Цель урока:

- повторение теоретического материала;

- обобщение навыка решения задач по данным темам.

Ход урока

I. Проверка домашнего задания

II. Повторение теоретического материала

Вопросы:

1. Какие прямые в пространстве называются параллельными?

2. Какие прямые называются скрещивающимися?

3. Сформулируйте теорему о существовании и единственности прямой параллельной данной.

4. Сформулируйте признак параллельности прямых.

5. Что значит: прямая и плоскость параллельны?

6. Сформулируйте признак параллельности прямой и плоскости.

7. Какие плоскости называются параллельными?

8. Сформулируйте признак параллельности плоскостей.

9. Докажите, что если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

10. Докажите, что отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

III. Решение задач

Задача № 103. На ребрах DA, DB и DC тетраэдра DABC отмечены точки М, N, Р так, что DM : МА = DN : NB = DP : PC (рис. 1).

Докажите, что плоскости MNP и ABC параллельны.

Найдите площадь ΔМNР, если площадь ΔАВС равна 10 см2 и DM : МА = 2 : 1.

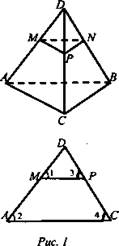
Решение:

1. Рассмотрим ΔADC и ΔMDP. По условию или отсюда Учитывая, что у треугольника ADC и треугольника MDP угол D - общий, a стороны, образующие угол D пропорциональны, делаем вывод ΔADC ~ ΔMDP. Из подобия следует равенство углов: ∠1 = ∠2; ∠3 = ∠4. Таким образом, МР || АС (по признаку параллельности прямых). Повторив рассуждение для грани DCB, получим PN || СВ. Следовательно, по теореме п. 10 (MNP) || (ABC).

2. ΔMNP ~ ΔАВС (по двум углам). Из подобия ΔADC и ΔMDP следует, что (Ответ: )

Задача № 104 (рис. 2). Изобразите тетраэдр ABCD и отметьте точку М на ребре АВ. Постройте сечение тетраэдра плоскостью, проходящей через точку М параллельно прямым АС и BD.

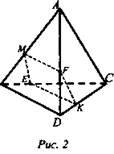
Решение: Проведем МЕ || АС, MF || BD. Плоскость сечения пересечет плоскость BCD по прямой параллельной MF (MF || (BCD) по построению), по этому проводим ЕК || BD. Соединим точки К и F. MEKF - искомое сечение. Докажем это.

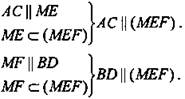
Итак, (MEKF) || AC, (MEKF) || BD.

Так как через точку М можно провести только одну прямую ME || АС в грани ABC и одну прямую MF || BD в грани BAD, то плоскость MEKF единственная.

IV. Математический диктант

Диктант по темам: «Аксиомы стереометрии» и «Параллельность прямых и плоскостей» (см. приложение).

Домашнее задание

П. 14. № 105, 108.

I уровень

Задача № 105 (рис. 3).

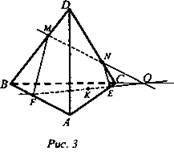
Решение: a) MN ВС. Продолжим отрезок MN до пересечения с продолжением стороны ВС в точке О. В плоскости ABC соединим точки О и К, он пересечет ребро АС в точке Е; продолжим отрезок ОК до пересечения с ребром АВ в точке F. Соединим точки М и F, лежащие в плоскости грани ABD и точки N и Е, лежащие в плоскости грани ADC.

Сечение MNEF - искомое.

б) MN || ВС (рис. 4).

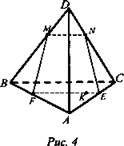
MN || ВС, ВС ⊂ плоскости ABC. По теореме I MN || плоскости ABC.

По теореме II плоскость сечения пересекает плоскость ABC, по прямой, проходящей через точку К параллельно MN.

Отсюда построение: в плоскости ABC через точку К проводим FE || ВС до пересечения со сторонами основания в точках F и Е. Соединяя точки М и F, точки N и Е, получаем искомое сечение MNEF.

II уровень

Задача № 108 (рис. 5).

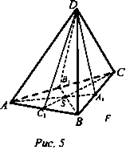
Решение: Отложим от точки D на ребрах DA, DB, DC равные отрезки: DA1’ = DB1’ = DC1’ = а. Соединим точки А1’, В1’ и С1’ отрезками (рис. 6). Нарисуем ограниченную этими отрезками часть тетраэдра, для удобства «положив» его на одну из плоскостей боковых граней.

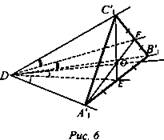
Проведем биссектрисы двух углов при вершине D: DE и DF, отрезки С1’Е и A1’F. В ΔA1’OB1' : DA1' = DB1', DE - общая. ∠A1’DE = ∠EDB1’, поэтому ΔA1’DE = ΔB1’DE. Следовательно, EA1’ = B1’E. В ΔC1’DB1’: DF - общая, DC1’ = DB1’ ∠C1’DF = ∠B1'DF, поэтому ΔC1’DF = ΔB1'DF, следовательно, C1’F = FB1'. В ΔA1’B1’C1’ отрезки C1’E и A1’F являются медианами.

Аналогично для биссектрисы из вершины В1’. Таким образом, плоскости DEC1’ и DFA1’ и третья, не показанная на рисунке, пересекаются на рисунке по прямой DO.

Раз указанные плоскости пересекаются по прямой DO, то эта прямая пересечется с плоскостью основания в некоторой точке S, значит, все три отрезка АА1’, СС1’ и ВВ1’ проходят через точку S.