Повторение по теме: «Объемы тел» - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ

Цели урока:

- организовать повторение основных теоретических фактов;

- проверить знание формул;

- повторить наиболее распространенные приемы решения задач;

- совершенствовать навыки решения задач, познакомить с некоторыми теоретическими факторами.

Ход урока

I. Организационный момент

Сообщить тему урока, цели урока.

II. Актуализация знаний учащихся

а) Рассмотреть таблицу, вспомнить формулы.

б) Напомнить, что отношение объемов подобных тел равно кубу коэффициента подобия, а отношение боковых поверхностей квадрату коэффициента подобия, т.е. и т. д.;

в) Вставить пропущенное (на крыльях доски заранее записаны формулы с пропущенными символами). 2 человека работают у доски. Оценивается лучшая работа.

Призма: где AA1 - боковое ребро.

Пирамида:

Усеченная пирамида: где S1, S2 - площади оснований.

Цилиндр: Шар: Конус:

III. Несколько полезных добавлений в копилку теоретических знаний (чертежи заготовлены заранее) (10 мин)

1) В каком отношении делится объем произвольной пирамиды плоскостью, проходящей через вершину пирамиды и пересекающей ее основание (рис. 1).

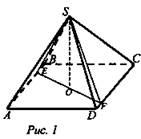
Для удобства, рассмотрим произвольную четырехугольную пирамиду. где Н = SO. ⇒ пирамиды имеют общую высоту (Ответ: )

2) В каком отношении делит объем пирамиды плоскость параллельная основанию и пересекающая боковые ребра (рис. 2).

V1 - объем усеченной пирамиды, V2 - объем верхней пирамиды, V - объем исходной пирамиды. Исходная пирамида и отсеченная верхняя пирамида подобны, поэтому а значит (Ответ: )

3) Доказать, что объем произвольного многогранника в который можно вписать шар радиуса R связан с площадью S„ поверхности этого многогранника формулой: (рис. 3).

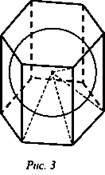
Соединим центр шара с вершинами многогранника. Многогранник разобьется на пирамиды, вершины которых будут центром шара, а основаниями грани многогранника, высоты всех пирамид будут равны радиусу шара (по св-ву касательной плоскости).

Тогда объем многогранника будет равен сумме объемов пирамид , что и требовалось доказать.

Прием разбиения тела на более простые часто используется при решении задач. Например: Центр куба, ребро которого а, соединен со всеми его вершинами. Определите объем каждой из полученных пирамид.

Решение: Восемь проведенных отрезков делят куб на 6 равных пирамид, поэтому

Какие еще методы регулярно используются? (устное обсуждение, выводы записать в тетрадь) (3 мин.)

IV. Методы решения

а) непосредственное нахождение элементов геометрического тела и нахождение неизвестного с помощью формул.

б) введение линейной или угловой неизвестной с последующим составлением уравнения.

в) использование свойств подобных тел, свойств сечений, свойства проекции плоского многоугольника ( где α - угол между плоскостями).

г) применение сведений о взаимном расположении тел в задачах на комбинацию нескольких тел.

д) векторно-координатный метод.

Чаще всего при решении задачи используют сразу несколько методов. Рассмотрим это на конкретных примерах.

V. Решение задач

(учащиеся с помощью магнитов вывешивают плакаты со своими решениями, рассказывают какие методы использованы) (20 мин.)

1. В правильном тетраэдре построено сечение его плоскостью, проходящей через ребро АС и точку К, принадлежащую ребру SB, причем ВК : KS = 2 : 1 (рис. 4).

Найти объем отсеченной пирамиды КАВС, если ребро тетраэдра равно а.

Дано: ABCS - тетраэдр; K ∈ BS; ВК : КС = 2 : 1; АВ = ВС = AC = AS = a.

Найти: VKABC.

Решение:

1) SO ⊥ (ABC); КО1 ⊥ (ABC) ⇒ SO || KO1, тогда SO ∈ (SBO) и КО1 ∈ (SBO) ⇒ O1 ∈ BO.

2) (BSO): по теореме о пропорцион. отрезках ВO1 : O1O = 2 : 1 ⇒ ΔKBO1 ~ ΔSВО (II призн. под.) ⇒

3) О - центр правильного треугольника ABC, значит

Из ΔSOB по теореме Пифагора

4)

(Ответ: Метод - последовательное нахождение элементов.)

2. Через сторону нижнего основания куба проведена плоскость, делящая объем куба в отношении m : n, считая от нижнего основания. Найти угол между плоскостью сечения и плоскостью основания, если m ≤ n.

Дано: ABCDA1B1C1D1 - куб; ABNM — сечение; (рис. 5).

Найти: ∠((ABN); (ABC)).

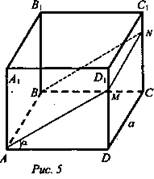
Решение:

1) Пусть АВ = CD = A1B1 = а, a ∠((ABN); (ABC)) = ∠MAD = α. ΔAMD : MD = atgα; MD1 = a - atgα.

2) AMDBNC - прямая треугольная призма с основаниями ΔAMD и ΔBNC и высотой a. AA1D1MBB1C1N - прямая четырехугольная призма с основаниями AA1D1M и BB1C1N и высотой a, V1 - объем треугольной призмы, V2 – объем четырехугольной призмы.

3) Решив уравнение, получим

(Ответ: Метод - введение вспомогательного линейного аргумента, решение уравнения.)

3. Боковая поверхность правильной четырехугольной пирамиды равна S, а двугранный угол при боковом ребре равен 120°. Найдите объем пирамиды.

Дано: ABCDL - правильная четырехугольная пирамида. Sбок.п. = S; ∠((ALD); (CLD)) = 120° (рис. 6).

Найти: Vпир.

Решение:

1) Проведем AK ⊥ LD. ΔADK = ΔCDK (по I призн.) ⇒ СК ⊥ LD ⇒ LD ⊥ (AKC) ⇒ ∠AKC - линейный угол при боковом ребре. По условию ∠AKC = 120° ⇒ ∠AKO = ∠CKO = 60°.

2) ΔOLD - проекция ΔALD на плоскость (BLD), значит, по свойству проекции многоугольника

3) Пусть АО = OD = b. ΔАОК:

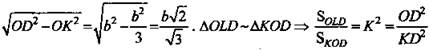
Таким образом,

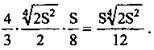
(Ответ: Метод - разбиение тела на части, введение вспомогательной переменной, теорема о проекции многоугольника.)

4. Основанием наклонного параллелепипеда случит ромб со стороной а и острым углом 30°. Диагональ одной боковой грани перпендикулярна плоскости основания, а боковое ребро составляет с плоскостью основания угол 60°. Найти объем параллелепипеда.

Дано: ABCDA1B1C1D1 - наклонный параллелепипед; ABCD - ромб; АВ = а; ∠A = 30°; AD ⊥ (ABC); ∠(AA1; (ABC)) = 60° (рис. 7).

Найти: Vпир.

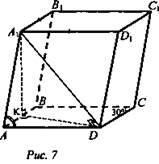
Решение: АВ = AD = а; ∠C = 30°; A1D ⊥ (ABC) ⇒ ∠(AA1; (ABC) = ∠A1AD = 60°.

Проведем A1K ⊥ AB, тогда по теореме о трех перпендикулярах DK ⊥ АВ и ΔAA1D:

(Ответ: Метод - последовательное вычисление величин.)

5. Пирамида MABCD задана координатами своих вершин: М(-1; 2; 5); А(1; -1; 2); В(-2; 1; 2); С(-1; 3; 2); D(3; 1; 2). Найти объем пирамиды.

Дано: MABCD - пирамида; M(-1; 2; 5); A(1; -1; 2); B(-2; 1; 2); С(-1; 3; 2); D(3; 1; 2).

Найти: Vпир.

1) Заметим, что аппликаты точек А, В, С, D равны между собой, т.е. Z = 2, значит основание пирамиды лежит в плоскости Z = 2. Т.к. аппликаты точки М : Z = 5, то расстояние от точки М до плоскости основания ABCD равно 5-2 = 3, значит Я = 3.

2) Пусть φ - угол между диагоналями основания, тогда

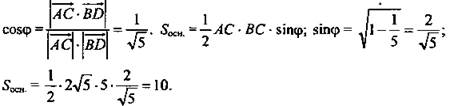
3)

(Ответ: 10 куб. ед. Метод - координатно-векторный.)

VI. Подведение итогов

Домашнее задание (5 мин)

а) выставление оценок.

б) указание к домашнему заданию (тесты заданий на партах с начала урока).

в) два ученика готовят решение на листах ватмана для проверки на следующем уроке.

Дома:

№ 1. Через точку, делящую ребро правильного тетраэдра в отношении 1 : 4, проведена плоскость, перпендикулярная этому ребру.

Найти отношение объемов полученных частей тетраэдра.

Дано: ABCD - тетраэдр; СК : КА = 1 : 4; AC ⊥ (KLM) (рис. 8).

Найти: VKLMC : VADBKLM.

Решение: СК : КА = 1 : 4. (LKM) ⊥ АС. Пусть СК = а, тогда АК = 4а; АС = 5а. Пусть N - середина АС. Тогда DN || KL; BN || КМ ⇒ (LKM) || (DNB). Пирамиды KLMC и NDBC подобны, поэтому отношение их объемов равно кубу их соответствующих линейных размеров. Поэтому a Тогда VKLMC : VADBKLM = 4 : 121. (Ответ: 4 : 121.)

№ 2. Основанием пирамиды служит ромб с острым углом 30°. Боковые грани наклонены к плоскости основания под углом 60°. Определить объем пирамиды, если радиус вписанного в ромб круга равен r.

Дано: ABCDS - пирамида, ABCD - ромб, ∠A = 30°. ∠((SDC) : (ABC)) = 60°. Все грани равнонаклонены к основанию ОК = r (рис. 9).

Найти: Vпир.

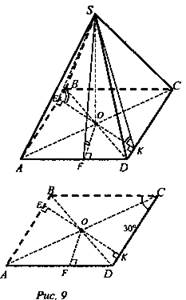
1) O - центр вписанной в ромб окружности, тогда ОЕ ⊥ АВ; OF ⊥ AD; OK ⊥ CD; SO ⊥ (ABCD) (так как если все боковые грани наклонены к плоскости основания под одним углом, то проекцией вершины пирамиды служит центр окружности вписанной в основание).

2) ∠SEO = ∠SFO = ∠SKO = 60° (по условию), ΔSEK: пусть AB = а, тогда с другой стороны

Получим уравнение